


ISSN 1004-132X
CN 42-1294/TH
CN 42-1294/TH



China Mechanical Engineering ›› 2025, Vol. 36 ›› Issue (11): 2685-2693.DOI: 10.3969/j.issn.1004-132X.2025.11.026
Qianhao LONG( ), Ying ZHOU, Liang GAO, Hao LI(
), Ying ZHOU, Liang GAO, Hao LI( )
)
Received:2024-06-19
Online:2025-11-25
Published:2025-12-09
Contact:
Hao LI
通讯作者:
李好
作者简介:龙千浩,男,2000年生,硕士研究生。研究方向为微结构拓扑优化设计。E-mail:m202270597@hust.edu.cn基金资助:CLC Number:
Qianhao LONG, Ying ZHOU, Liang GAO, Hao LI. Fast Prediction of Microstructure Performance Based on 3D Convolutional Neural Network[J]. China Mechanical Engineering, 2025, 36(11): 2685-2693.
龙千浩, 周颖, 高亮, 李好. 基于三维卷积神经网络的微结构性能快速预测[J]. 中国机械工程, 2025, 36(11): 2685-2693.
Add to citation manager EndNote|Ris|BibTeX
URL: https://www.cmemo.org.cn/EN/10.3969/j.issn.1004-132X.2025.11.026
| 序号 | 结构 | 本层输入、输出的数据维度 |
|---|---|---|
| 1 | 卷积块1 | (2×40×40×40)、(2×20×20×20) |
| 2 | 卷积块2 | (2×20×20×20)、(2×10×10×10) |
| 3 | 卷积块3 | (2×10×10×10)、(2×5×5×5) |
| 4 | 全连接层1 | (2×5×5×5)、128 |
| 5 | 全连接层2 | 128、64 |
| 6 | 全连接层3 | 64、32 |
| 7 | 全连接层4 | 32、3 |
Tab.2 Main architecture of 3D convolutional neural network
| 序号 | 结构 | 本层输入、输出的数据维度 |
|---|---|---|
| 1 | 卷积块1 | (2×40×40×40)、(2×20×20×20) |
| 2 | 卷积块2 | (2×20×20×20)、(2×10×10×10) |
| 3 | 卷积块3 | (2×10×10×10)、(2×5×5×5) |
| 4 | 全连接层1 | (2×5×5×5)、128 |
| 5 | 全连接层2 | 128、64 |
| 6 | 全连接层3 | 64、32 |
| 7 | 全连接层4 | 32、3 |
| 微结构 | 体积 分数/ % | 三维卷积网络 预测结果 | 数值均质化 计算结果 | 相对 误差/ % |
|---|---|---|---|---|
 | 11 | (3.99,3.44,3.17) | (4.03,3.45,3.13) | 0.85 |
| 23 | (11.27,8.35,7.48) | (11.18,8.43,7.66) | 1.37 | |
| 35 | (22.15,14.29,13.18) | (22.31,14.14,13.12) | 0.75 | |
| 47 | (40.12,20.98,19.91) | (39.51,20.63,19.73) | 1.38 | |
| 59 | (66.91,28.84,28.22) | (66.22,28.68,27.95) | 0.86 | |
 | 11 | (9.75, 0.76,0.38) | (9.78,0.75,0.39) | 1.40 |
| 23 | (22.19,2.48,1.63) | (22.23,2.41,1.67) | 1.83 | |
| 35 | (38.25,5.63,4.69) | (38.37,5.56,4.76) | 1.01 | |
| 47 | (59.23,11.15.10.49) | (59.34,11.04.10.57) | 0.65 | |
| 59 | (86.28,20.73,19.97) | (87.01,20.45,19.89) | 0.87 | |
 | 11 | (6.26,2.75,2.49) | (6.13,2.84,2.56) | 2.67 |
| 23 | (15.26,6.42,5.78) | (14.93,6.25,5.68) | 2.23 | |
| 35 | (29.25,10.32,10.25) | (28.93,10.65,10.02) | 2.17 | |
| 47 | (48.93,16.12,15.63) | (48.67,15.99,15.55) | 0.62 | |
| 59 | (76.24,23.46,22.71) | (76.62,23.67,23.02) | 0.91 | |
 | 11 | (5.45,3.11,2.94) | (5.37,3.19,2.89) | 1.91 |
| 23 | (13.57,7.47,6.85) | (13.49,7.54,6.78) | 0.85 | |
| 35 | (25.79,12.82,12.25) | (25.78,12.97,11.96) | 1.21 | |
| 47 | (43.85,19.36,18.44) | (43.38,19.08,18.29) | 1.12 | |
| 59 | (71.26,27.65,26.99) | (70.61,27.36,26.82) | 0.87 | |
 | 11 | (6.91,2.56,2.29) | (6.77,2.47,2.22) | 2.95 |
| 23 | (15.88,6.56,5.98) | (15.60,6.46,5.91) | 1.51 | |
| 35 | (28.73,11.35,10.62) | (28.99,11.52,10.84) | 1.47 | |
| 47 | (47.74,18.21,17.35) | (47.19,17.92,17.32) | 1.54 | |
| 59 | (74.63,27.54,26.75) | (74.26,27.22,26.40) | 1.00 |
Tab.3 The independent parameter vectors of the equivalent elastic tensors predicted by the 3D convolutional network and their relative errors
| 微结构 | 体积 分数/ % | 三维卷积网络 预测结果 | 数值均质化 计算结果 | 相对 误差/ % |
|---|---|---|---|---|
 | 11 | (3.99,3.44,3.17) | (4.03,3.45,3.13) | 0.85 |
| 23 | (11.27,8.35,7.48) | (11.18,8.43,7.66) | 1.37 | |
| 35 | (22.15,14.29,13.18) | (22.31,14.14,13.12) | 0.75 | |
| 47 | (40.12,20.98,19.91) | (39.51,20.63,19.73) | 1.38 | |
| 59 | (66.91,28.84,28.22) | (66.22,28.68,27.95) | 0.86 | |
 | 11 | (9.75, 0.76,0.38) | (9.78,0.75,0.39) | 1.40 |
| 23 | (22.19,2.48,1.63) | (22.23,2.41,1.67) | 1.83 | |
| 35 | (38.25,5.63,4.69) | (38.37,5.56,4.76) | 1.01 | |
| 47 | (59.23,11.15.10.49) | (59.34,11.04.10.57) | 0.65 | |
| 59 | (86.28,20.73,19.97) | (87.01,20.45,19.89) | 0.87 | |
 | 11 | (6.26,2.75,2.49) | (6.13,2.84,2.56) | 2.67 |
| 23 | (15.26,6.42,5.78) | (14.93,6.25,5.68) | 2.23 | |
| 35 | (29.25,10.32,10.25) | (28.93,10.65,10.02) | 2.17 | |
| 47 | (48.93,16.12,15.63) | (48.67,15.99,15.55) | 0.62 | |
| 59 | (76.24,23.46,22.71) | (76.62,23.67,23.02) | 0.91 | |
 | 11 | (5.45,3.11,2.94) | (5.37,3.19,2.89) | 1.91 |
| 23 | (13.57,7.47,6.85) | (13.49,7.54,6.78) | 0.85 | |
| 35 | (25.79,12.82,12.25) | (25.78,12.97,11.96) | 1.21 | |
| 47 | (43.85,19.36,18.44) | (43.38,19.08,18.29) | 1.12 | |
| 59 | (71.26,27.65,26.99) | (70.61,27.36,26.82) | 0.87 | |
 | 11 | (6.91,2.56,2.29) | (6.77,2.47,2.22) | 2.95 |
| 23 | (15.88,6.56,5.98) | (15.60,6.46,5.91) | 1.51 | |
| 35 | (28.73,11.35,10.62) | (28.99,11.52,10.84) | 1.47 | |
| 47 | (47.74,18.21,17.35) | (47.19,17.92,17.32) | 1.54 | |
| 59 | (74.63,27.54,26.75) | (74.26,27.22,26.40) | 1.00 |
| 训练构型 | 神经网络预测结果 | 数值均值化结果 | ||
|---|---|---|---|---|
| 弹性模量 | 剪切模量 | 弹性模量 | 剪切模量 | |
 |
Emax=4.37 GPa, Emin=0.69 GPa |
Gmax=1.87 GPa, Gmin=0.33 GPa |
Emax=4.43 GPa, Emin=0.72 GPa |
Gmax=1.89 GPa, Gmin=0.35 GPa |
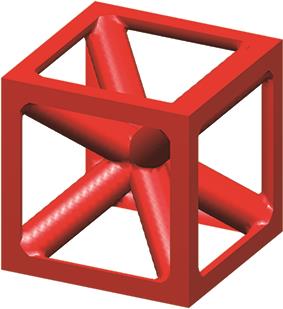 |
Emax=5.77 GPa, Emin=5.53 GPa |
Gmax=2.29 GPa, Gmin=2.21 GPa |
Emax=5.60 GPa, Emin=6.45 GPa |
Gmax=2.22 GPa, Gmin=2.17 GPa |
 |
Emax=18.29 GPa, Emin=8.71 GPa |
Gmax=7.58 GPa, Gmin=3.96 GPa |
Emax=18.45 GPa, Emin=8.78 GPa |
Gmax=7.65 GPa, Gmin=4.00 GPa |
 |
Emax=12.14 GPa, Emin=11.44 GPa |
Gmax=4.73 GPa, Gmin=4.52 GPa |
Emax=12.21 GPa, Emin=11.74 GPa |
Gmax=4.80 GPa, Gmin=4.65 GPa |
Tab.4 Mechanical images of convolution network and numerical homogenization calculation results
| 训练构型 | 神经网络预测结果 | 数值均值化结果 | ||
|---|---|---|---|---|
| 弹性模量 | 剪切模量 | 弹性模量 | 剪切模量 | |
 |
Emax=4.37 GPa, Emin=0.69 GPa |
Gmax=1.87 GPa, Gmin=0.33 GPa |
Emax=4.43 GPa, Emin=0.72 GPa |
Gmax=1.89 GPa, Gmin=0.35 GPa |
 |
Emax=5.77 GPa, Emin=5.53 GPa |
Gmax=2.29 GPa, Gmin=2.21 GPa |
Emax=5.60 GPa, Emin=6.45 GPa |
Gmax=2.22 GPa, Gmin=2.17 GPa |
 |
Emax=18.29 GPa, Emin=8.71 GPa |
Gmax=7.58 GPa, Gmin=3.96 GPa |
Emax=18.45 GPa, Emin=8.78 GPa |
Gmax=7.65 GPa, Gmin=4.00 GPa |
 |
Emax=12.14 GPa, Emin=11.44 GPa |
Gmax=4.73 GPa, Gmin=4.52 GPa |
Emax=12.21 GPa, Emin=11.74 GPa |
Gmax=4.80 GPa, Gmin=4.65 GPa |
| 数值均质化方法 | 三维卷积神经网络 | |
|---|---|---|
| 总耗时 | 3445.6 | 2.1 |
| 单个耗时 | 34.46 | 0.02 |
Tab.5 Consuming time in calculation of 100 microstructures
| 数值均质化方法 | 三维卷积神经网络 | |
|---|---|---|
| 总耗时 | 3445.6 | 2.1 |
| 单个耗时 | 34.46 | 0.02 |
| 训练构型 | 神经网络预测结果 | 数值均值化结果 | ||
|---|---|---|---|---|
| 弹性模量 | 剪切模量 | 弹性模量 | 剪切模量 | |
 |
Emax=3.80 GPa, Emin=0.46 GPa |
Gmax=0.54 GPa, Gmin=0.16 GPa |
Emax=3.83 GPa, Emin=0.49 GPa |
Gmax=0.55 GPa, Gmin=0.17 GPa |
 |
Emax=2.37 GPa, Emin=1.64 GPa |
Gmax=0.96 GPa, Gmin=0.71 GPa |
Emax=2.44 GPa, Emin=1.65 GPa |
Gmax=0.99 GPa, Gmin=0.717 GPa |
Tab.6 Mechanical images of test subjects
| 训练构型 | 神经网络预测结果 | 数值均值化结果 | ||
|---|---|---|---|---|
| 弹性模量 | 剪切模量 | 弹性模量 | 剪切模量 | |
 |
Emax=3.80 GPa, Emin=0.46 GPa |
Gmax=0.54 GPa, Gmin=0.16 GPa |
Emax=3.83 GPa, Emin=0.49 GPa |
Gmax=0.55 GPa, Gmin=0.17 GPa |
 |
Emax=2.37 GPa, Emin=1.64 GPa |
Gmax=0.96 GPa, Gmin=0.71 GPa |
Emax=2.44 GPa, Emin=1.65 GPa |
Gmax=0.99 GPa, Gmin=0.717 GPa |
| [1] | 卢天健, 何德坪, 陈常青, 等. 超轻多孔金属材料的多功能特性及应用[J]. 力学进展, 2006, 36(4): 517-535. |
| LU Tianjian, HE Deping, CHEN Changqing, et al. The Multi-functionality of Ultra-light Porous Metals and Their Applications[J]. Advances in Mechanics, 2006, 36(4): 517-535. | |
| [2] | 熊健, 杜昀桐, 杨雯, 等. 轻质复合材料夹芯结构设计及力学性能最新进展[J]. 宇航学报, 2020, 41(6): 749-760. |
| XIONG Jian, DU Yuntong, YANG Wen, et al. Research Progress on Design and Mechanical Properties of Lightweight Composite Sandwich Structures[J]. Journal of Astronautics, 2020, 41(6): 749-760. | |
| [3] | 雷红帅, 赵则昂, 郭晓岗, 等. 航天器轻量化多功能结构设计与制造技术研究进展[J]. 宇航材料工艺, 2021, 51(4): 10-22. |
| LEI Hongshuai, ZHAO Zeang, GUO Xiaogang, et al. Research Progress on the Design and Manufacture Technology of Lightweight Multifunctional Spacecraft Structures[J]. Aerospace Materials & Technology, 2021, 51(4): 10-22. | |
| [4] | SAEB S, STEINMANN P, JAVILI A. Aspects of Computational Homogenization at Finite Deformations: a Unifying Review from Reuss' to Voigt's Bound[J]. Applied Mechanics Reviews, 2016, 68(5): 050801. |
| [5] | HASHIN Z, SHTRIKMAN S. A Variational Approach to the Theory of the Effective Magnetic Permeability of Multiphase Materials[J]. Journal of Applied Physics, 1962, 33(10): 3125-3131. |
| [6] | MORI T, TANAKA K. Average Stress in Matrix and Average Elastic Energy of Materials with Misfitting Inclusions[J]. Acta Metallurgica, 1973, 21(5): 571-574. |
| [7] | BENVENISTE Y. A New Approach to the Application of Mori-Tanaka's Theory in Composite Materials[J]. Mechanics of Materials, 1987, 6(2): 147-157. |
| [8] | KRÖNER E. Berechnung Der Elastischen Konstanten des Vielkristalls Aus Den Konstanten des Einkristalls[J]. Zeitschrift Für Physik, 1958, 151(4): 504-518. |
| [9] | WILLIS J R. Bounds and Self-consistent Estimates for the Overall Properties of Anisotropic Composites[J]. Journal of the Mechanics and Physics of Solids, 1977, 25(3): 185-202. |
| [10] | KERNER E H. The Elastic and Thermo-elastic Properties of Composite Media[J]. Proceedings of the Physical Society Section B, 1956, 69(8): 808-813. |
| [11] | CHATZIGEORGIOU G, SEIDEL G D, LAGOUDAS D C. Effective Mechanical Properties of “Fuzzy Fiber” Composites[J]. Composites Part B: Engineering, 2012, 43(6): 2577-2593. |
| [12] | 蔡园武. 周期性板结构的渐近均匀化方法及微结构优化[D]. 大连: 大连理工大学, 2014. |
| CAI Yuanwu. Asymptotic Homogenization of Periodic Plate and Micro-structural Optimization[D]. Dalian: Dalian University of Technology, 2014. | |
| [13] | HASSANI B, HINTON E. A Review of Homogenization and Topology Optimization I—Homogenization Theory for Media with Periodic Structure[J]. Computers & Structures, 1998, 69(6): 707-717. |
| [14] | 张永存, 尚士朋, 梁宇静. 周期性复合材料等效传热系数预测的渐进均匀化新算法及其实现[J]. 复合材料学报, 2018, 35(1): 208-217. |
| ZHANG Yongcun, SHANG Shipeng, LIANG Yujing. A New Algorithm of Asymptotic Homogenization Method for Predicting the Effective Thermal Conductivity and Its Implementation of Periodic Composite Materials[J]. Acta Materiae Compositae Sinica, 2018, 35(1): 208-217. | |
| [15] | SCHUMACHER C, BICKEL B, RYS J, et al. Microstructures to Control Elasticity in 3D Printing[J]. ACM Transactions on Graphics, 2015, 34(4): 1-13. |
| [16] | PANETTA J, ZHOU Qingnan, MALOMO L, et al. Elastic Textures for Additive Fabrication[J]. ACM Transactions on Graphics, 2015, 34(4): 1-12. |
| [17] | MARTÍNEZ J, DUMAS J, LEFEBVRE S. Procedural Voronoi Foams for Additive Manufacturing[J]. ACM Transactions on Graphics, 2016, 35(4): 1-12. |
| [18] | TEMIZER İ, WRIGGERS P. An Adaptive Method for Homogenization in Orthotropic Nonlinear Elasticity[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(35/36): 3409-3423. |
| [19] | YVONNET J, GONZALEZ D, HE Q C. Numerically Explicit Potentials for the Homogenization of Nonlinear Elastic Heterogeneous Materials[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(33/36): 2723-2737. |
| [20] | YVONNET J, MONTEIRO E, HE Qichang. Computational Homogenization Method and Reduced Database Model for Hyperelastic Heterogeneous Structures[J]. International Journal for Multiscale Computational Engineering, 2013, 11(3): 201-225. |
| [21] | LIU Peiqing, LIU An, PENG Hao, et al. Mechanical Property Profiles of Microstructures via Asymptotic Homogenization[J]. Computers & Graphics, 2021, 100: 106-115. |
| [22] | FRITZEN F, KUNC O. Two-stage Data-driven Homogenization for Nonlinear Solids Using a Reduced Order Model[J]. European Journal of Mechanics—A/Solids, 2018, 69: 201-220. |
| [23] | LE B A, YVONNET J, HE Q C. Computational Homogenization of Nonlinear Elastic Materials Using Neural Networks[J]. International Journal for Numerical Methods in Engineering, 2015, 104(12): 1061-1084. |
| [24] | LU Xiaoxin, GIOVANIS D G, YVONNET J, et al. A Data-driven Computational Homogenization Method Based on Neural Networks for the Nonlinear Anisotropic Electrical Response of Graphene/Polymer Nanocomposites[J]. Computational Mechanics, 2019, 64(2): 307-321. |
| [25] | BERMEJILLO BARRERA M D, FRANCO-MARTÍNEZ F, DÍAZ LANTADA A. Artificial Intelligence Aided Design of Tissue Engineering Scaffolds Employing Virtual Tomography and 3D Convolutional Neural Networks[J]. Materials, 2021, 14(18): 5278. |
| [26] | WU Peichen, IQUEBAL A S, ANKIT K. Emulating Microstructural Evolution during Spinodal Decomposition Using a Tensor Decomposed Convolutional and Recurrent Neural Network[J]. Computational Materials Science, 2023, 224: 112187. |
| [27] | ZHENG Li, KUMAR S, KOCHMANN D M. Data-driven Topology Optimization of Spinodoid Metamaterials with Seamlessly Tunable Anisotropy[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 383: 113894. |
| [28] | ZHENG Xiaoyang, CHEN Tate, GUO Xiaofeng, et al. Controllable Inverse Design of Auxetic Metamaterials Using Deep Learning[J]. Materials & Design, 2021, 211: 110178. |
| [29] | DONG Jiaqi, QIN Qinghua, XIAO Yi. Nelder-mead Optimization of Elastic Metamaterials via Machine-learning-aided Surrogate Modeling[J]. International Journal of Applied Mechanics, 2020, 12(1): 2050011. |
| [30] | ANDREASSEN E, ANDREASEN C S. How to Determine Composite Material Properties Using Numerical Homogenization[J]. Computational Materials Science, 2014, 83: 488-495. |
| [1] |
LI Xiao-Li, CHEN Wei, YAN Rong.
Adaptive Compensation of Contour Errors Based on BP Neural Networks
[J]. J4, 201016, 21(16): 1902-1906.
|
| [2] |
DIAO Wei, WANG Zhi-Yuan, ZHOU Zhi-Li.
Simulation Research on Truck Braking Stability on Turn of an Continuous Downgrade
[J]. J4, 201016, 21(16): 2010-2015.
|
| [3] | Jianjian WANG, Yuhe LIAO, Lei YANG, Jiutao XUE. Rotor Unbalance Recognition Based on Multidimensional Complex Feature Fusion and CNN-GRU [J]. China Mechanical Engineering, 2025, 36(9): 1905-1915. |
| [4] | Hongwei XU, Wenbin YE, Shunyao MA, Hang ZHANG. Research on Color Matching Calibration Algorithm for FDM Full Color 3D Presses [J]. China Mechanical Engineering, 2025, 36(9): 2081-2086. |
| [5] | Haiyan XING, Xueyuan WU, Zhihui CAI, Liwei ZHAO, Tian SU, Qing HAN. Quantitative Identification of Oil and Gas Pipeline Defect Levels Based on Magnetic Memory Using ResGNNet Multi-modal Fusions [J]. China Mechanical Engineering, 2025, 36(9): 2150-2157. |
| [6] | Zitong YUE, Yanting LI, Yu ZHAO. Condition Monitoring of Wind Turbines Based on Neural Networks and Robust Estimation [J]. China Mechanical Engineering, 2025, 36(8): 1842-1852. |
| [7] | Zhibo CHEN, Guoping LI, Sitong XIANG, Yanding WEI. Dynamic Perception and Experimental Study of Tactile Texture Based on Ultrasonic Resonance Squeeze Film Effect [J]. China Mechanical Engineering, 2025, 36(11): 2574-2582. |
| [8] | Jiaxiang DONG, Quanquan LIU, Xiping HU, Xuezhi ZHAO. Kinematic Modeling of a Novel Rigid⁃Flexible Hybrid Continuum Robots [J]. China Mechanical Engineering, 2025, 36(11): 2678-2684. |
| [9] | NI Jing1, LU Die1, MENG Zhen1, LIN Shaorong1, WANG Yang1, FU Yun2. Correlation Mechanism between Geometric Accuracy and Wettability Performance of Laser-induced Micro-structures [J]. China Mechanical Engineering, 2025, 36(07): 1423-1429,1561. |
| [10] | WANG Yahui1, 2, 3, HUANG Liang1, 2, LIU Xiang1, 2. Effects of Solution Treatment on Microstructure and Mechanics Properties of TC4 Titanium Alloy Parts Formed by Forging/Additive Manufacturing Composite Forming [J]. China Mechanical Engineering, 2025, 36(06): 1314-1321. |
| [11] | YANG Heran1, 2, ZHANG Peijie1, 2, SUN Xingwei1, 2, PAN Fei1, 2, LIU Yin1, 2. Surface Roughness Prediction for Screw Belt Grinding Based on Improved CNN [J]. China Mechanical Engineering, 2025, 36(02): 325-332. |
| [12] | CUI Xiaohui1, 2, YU Zhuoxing1, XIAO Ang3, YAN Ziqin4, YANG Guang1, WANG Hanpeng1, LI Rui1. Effects of Instantaneous Currents and Subsequent Aging Processes on Mechanics Properties and Microstructure of 7075 Aluminum Alloys [J]. China Mechanical Engineering, 2024, 35(12): 2139-2148. |
| [13] | GUO Haiyu1, ZOU Shenggong1, ZHANG Xiaoguang2, 3, 4, LU Fanfan2CHEN Yang2, WANG Han2, XU Xinzhi2. Fault Diagnosis of Rotating Machinery Bearings Based on Multi-source Wavelet Transform Neural Network [J]. China Mechanical Engineering, 2024, 35(11): 2026-2034. |
| [14] | WU Menghua1, JIANG Bingchun1, XIAO Yuqing2, JIA Weiping2. Effects of Magnetic Fields on Growth Pattern of Three-dimensional Microstructures in MLED-AM [J]. China Mechanical Engineering, 2024, 35(11): 2035-2042. |
| [15] | YANG Haifeng1, 2, SUN Xinhui1, 2, YUAN Dongqing3, ZHAO Enlan1, 4, LIU Songyong1, 2, PENG Yuxing1, 2. Microstructure and Ultrasonic Rolling Hardening Mechanism of Laser Wire Feeding Cladding High Manganese Steel Coatings [J]. China Mechanical Engineering, 2024, 35(11): 2043-2053,2081. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||