


ISSN 1004-132X
CN 42-1294/TH
CN 42-1294/TH



中国机械工程 ›› 2025, Vol. 36 ›› Issue (9): 1951-1960.DOI: 10.3969/j.issn.1004-132X.2025.09.006
• 机械基础工程 • 上一篇
黄宁宁1( ), 尤晶晶1,2(
), 尤晶晶1,2( ), 叶鹏达3, 沈惠平3, 李成刚4, 吴洪涛4
), 叶鹏达3, 沈惠平3, 李成刚4, 吴洪涛4
收稿日期:2024-06-10
出版日期:2025-09-25
发布日期:2025-10-15
通讯作者:
尤晶晶
作者简介:黄宁宁,男,1999年生,硕士研究生。研究方向为并联机器人机构学。E-mail:huangningning1819@163.com。
基金资助:
Ningning HUANG1( ), Jingjing YOU1,2(
), Jingjing YOU1,2( ), Pengda YE3, Huiping SHEN3, Chenggang LI4, Hongtao WU4
), Pengda YE3, Huiping SHEN3, Chenggang LI4, Hongtao WU4
Received:2024-06-10
Online:2025-09-25
Published:2025-10-15
Contact:
Jingjing YOU
摘要:
六自由度并联机构的正运动学方程非线性且强耦合,一般不具有符号式正解,不利于机器人的实时反馈控制。设计了一种在结构上弱耦合但在运动上可解耦的“7-4”式Stewart型并联机构,解析求解了正运动学方程和杆长协调方程,并开展了奇异性研究。基于“2-1”式运动链综合出六自由度“7-4”式Stewart型并联机构,并基于方位特征集理论,分析了机构的结构耦合特性。基于13个相容方程并运用四面体几何理论,提出了正运动学方程的一种解析求解算法,同时还证明出一般位形下实数解的个数为8(它们两两关于同一平面对称)。根据动球铰之间的几何约束关系,构建了杆长协调方程,研究发现,该方程也具有符号解。推导了机构的Jacobian矩阵,并分析了各种奇异类型。剖析了并联机构正运动学与奇异性之间的内在联系。
中图分类号:
黄宁宁, 尤晶晶, 叶鹏达, 沈惠平, 李成刚, 吴洪涛. 一种运动可解耦的Stewart型并联机构的正运动学及奇异性[J]. 中国机械工程, 2025, 36(9): 1951-1960.
Ningning HUANG, Jingjing YOU, Pengda YE, Huiping SHEN, Chenggang LI, Hongtao WU. Forward Kinematics and Singularity of Kinematically Decoupled Stewart-type Parallel Mechanisms[J]. China Mechanical Engineering, 2025, 36(9): 1951-1960.
| 组别 | Q4 | Q1 | Q2 |
|---|---|---|---|
| 1 | (1)Q4 | (1)Q1(1) | (1)Q2(1) |
| 2 | (1)Q2(2) | ||
| 3 | (1)Q1(2) | (1)Q2(3) | |
| 4 | (1)Q2(4) | ||
| 5 | (2)Q4 | (2)Q1(1) | (2)Q2(1) |
| 6 | (2)Q2(2) | ||
| 7 | (2)Q1(2) | (2)Q2(3) | |
| 8 | (2)Q2(4) |
表1 正运动学方程的多解性
Tab.1 Multiple solutions of forward kinematics
| 组别 | Q4 | Q1 | Q2 |
|---|---|---|---|
| 1 | (1)Q4 | (1)Q1(1) | (1)Q2(1) |
| 2 | (1)Q2(2) | ||
| 3 | (1)Q1(2) | (1)Q2(3) | |
| 4 | (1)Q2(4) | ||
| 5 | (2)Q4 | (2)Q1(1) | (2)Q2(1) |
| 6 | (2)Q2(2) | ||
| 7 | (2)Q1(2) | (2)Q2(3) | |
| 8 | (2)Q2(4) |
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|---|---|
| M1 | 20.000 | M4 | 50.000 | L4 | 67.823 |
| M1* | 40.000 | M4* | 70.000 | L4* | 86.023 |
| x′ | 0.000 | L1 | 38.356 | N1 | 30.000 |
| y′ | 30.000 | L1* | 35.323 | N2 | 42.426 |
| z′ | 0.000 | L2 | 35.868 | N3 | 42.426 |
| M3 | 40.000 | L3 | 43.111 | ||
| M3* | 60.000 | L3* | 56.878 | ||
表2 结构参数及输入参数
Tab.2 Mechanism parameters and input parameters mm
| 参数 | 数值 | 参数 | 数值 | 参数 | 数值 |
|---|---|---|---|---|---|
| M1 | 20.000 | M4 | 50.000 | L4 | 67.823 |
| M1* | 40.000 | M4* | 70.000 | L4* | 86.023 |
| x′ | 0.000 | L1 | 38.356 | N1 | 30.000 |
| y′ | 30.000 | L1* | 35.323 | N2 | 42.426 |
| z′ | 0.000 | L2 | 35.868 | N3 | 42.426 |
| M3 | 40.000 | L3 | 43.111 | ||
| M3* | 60.000 | L3* | 56.878 | ||
| 第1、5组解对称 | 第2、6组解对称 |
|---|---|
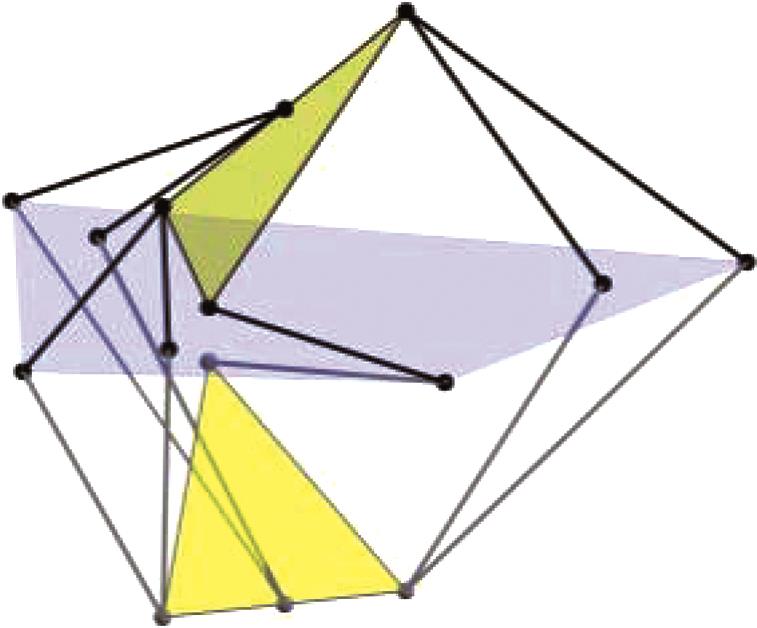 | 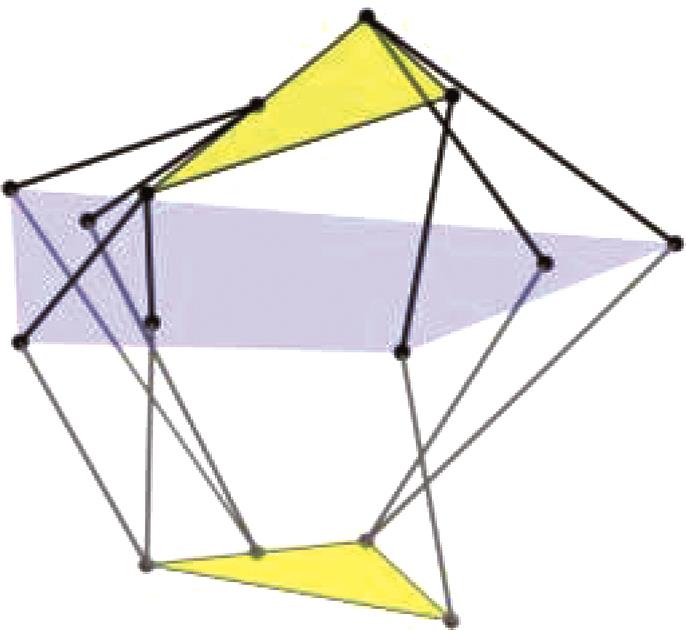 |
| 第3、7组解对称 | 第4、8组解对称 |
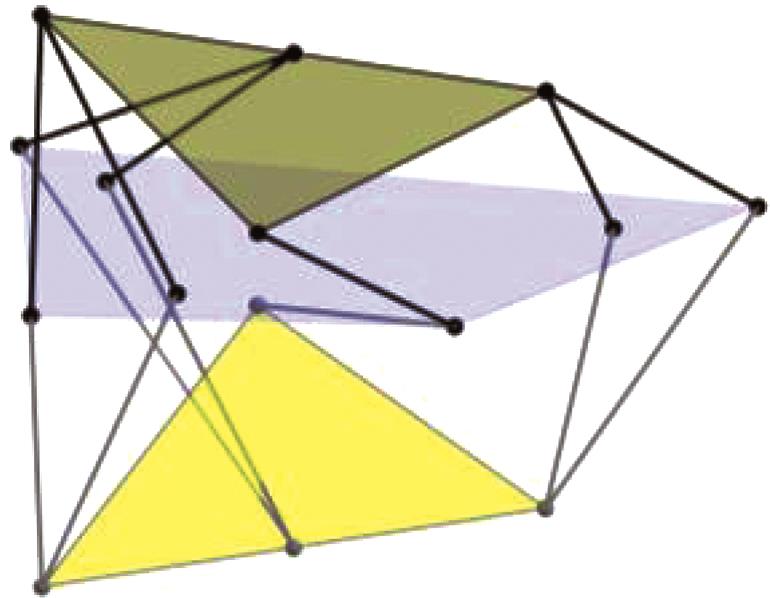 | 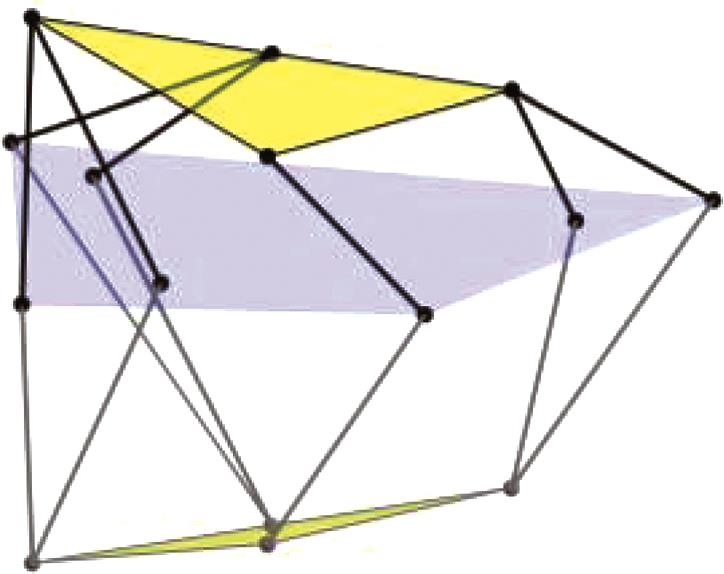 |
表3 机构位形简图
Tab.3 Schematic diagram of mechanism configuration
| 第1、5组解对称 | 第2、6组解对称 |
|---|---|
 |  |
| 第3、7组解对称 | 第4、8组解对称 |
 |  |
| 任意选取的数据/mm | 理论计算/mm | 试验测量/mm | |||||
|---|---|---|---|---|---|---|---|
| L1* | L3 | L3* | L4 | L4* | L1 | ||
| 1 | 35.322 97 | 43.1105 4 | 56.877 73 | 67.823 30 | 86.023 25 | 38.353 63 | 38.353 63 |
| 2 | 40.176 93 | 59.772 10 | 72.626 50 | 75.952 01 | 94.417 73 | 34.857 32 | 34.857 32 |
| 3 | 46.904 13 | 103.453 64 | 114.832 72 | 100.749 83 | 117.764 71 | 43.452 25 | 43.452 25 |
表4 理论计算与试验测量数据
Tab.4 Theoretical calculation and experimental measurement data
| 任意选取的数据/mm | 理论计算/mm | 试验测量/mm | |||||
|---|---|---|---|---|---|---|---|
| L1* | L3 | L3* | L4 | L4* | L1 | ||
| 1 | 35.322 97 | 43.1105 4 | 56.877 73 | 67.823 30 | 86.023 25 | 38.353 63 | 38.353 63 |
| 2 | 40.176 93 | 59.772 10 | 72.626 50 | 75.952 01 | 94.417 73 | 34.857 32 | 34.857 32 |
| 3 | 46.904 13 | 103.453 64 | 114.832 72 | 100.749 83 | 117.764 71 | 43.452 25 | 43.452 25 |
| aj | |
|---|---|
| b1 | |
| d1 | |
| a2 | |
| b2 | |
| d2 | |
| ae | |
| b3 | |
| d3 | |
| a4 | |
| bh | |
| d4 | |
| Bj | |
| Dj | |
| Be | |
| De | |
| A2 | |
| B2 | |
| D2 |
表5 J 中部分元素的解析式
Tab.5 Some elements in J
| aj | |
|---|---|
| b1 | |
| d1 | |
| a2 | |
| b2 | |
| d2 | |
| ae | |
| b3 | |
| d3 | |
| a4 | |
| bh | |
| d4 | |
| Bj | |
| Dj | |
| Be | |
| De | |
| A2 | |
| B2 | |
| D2 |
| 四组位置正解 | 一组位置正解 | ||
|---|---|---|---|
| 构型 | 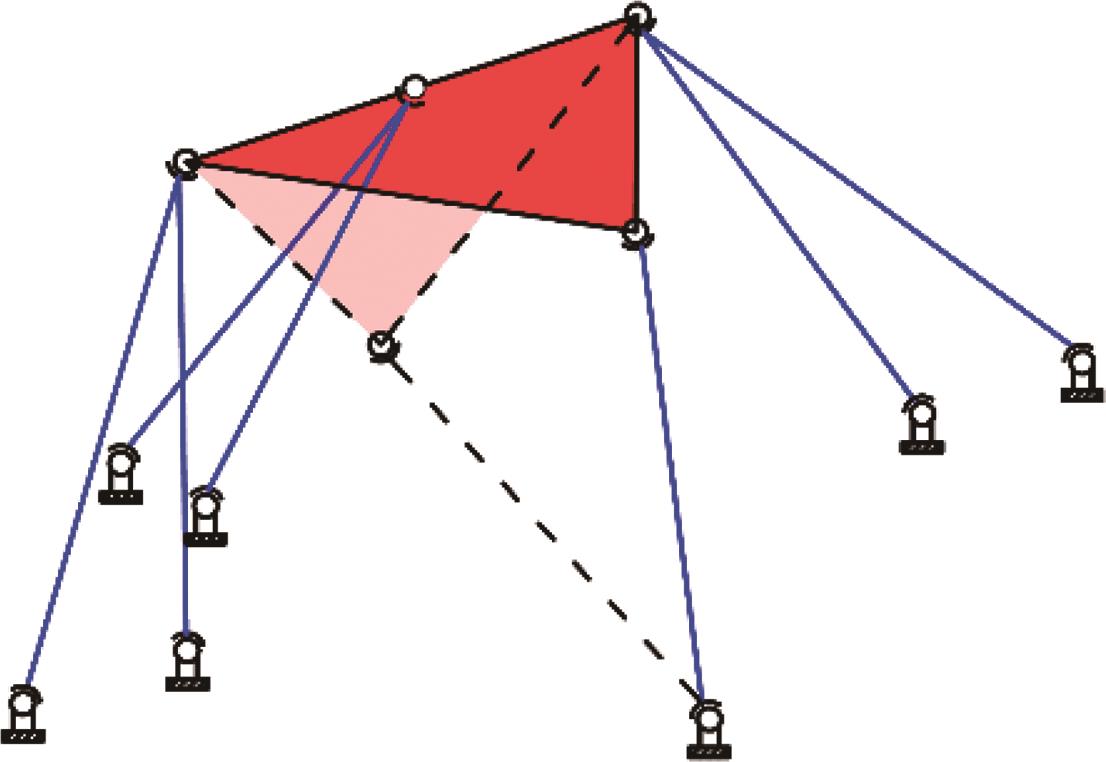 | 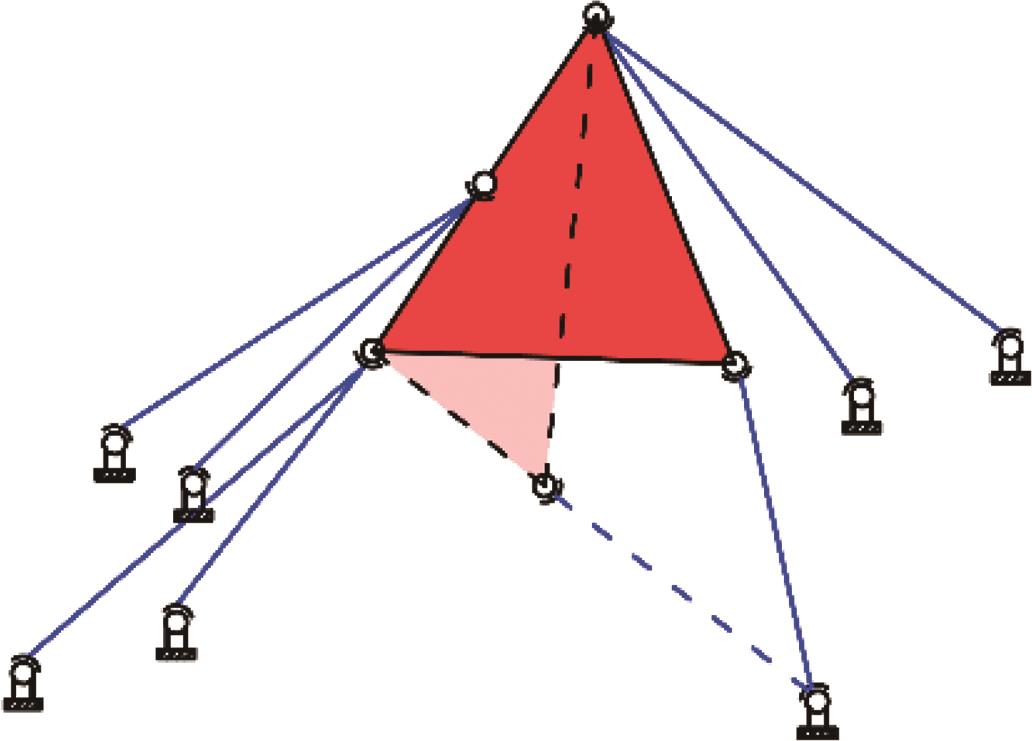 | 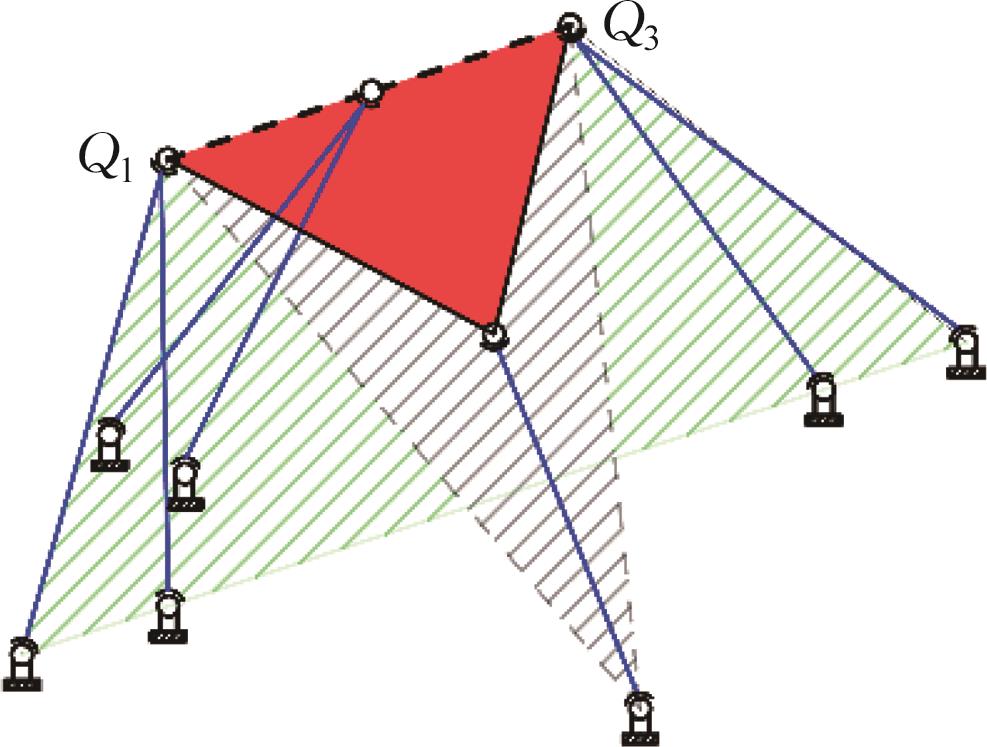 |
| 奇异 | 无奇异位形 | Hunt奇异,Q1Q3为瞬时旋转轴 | |
| 两组位置正解 | |||
| 构型 | 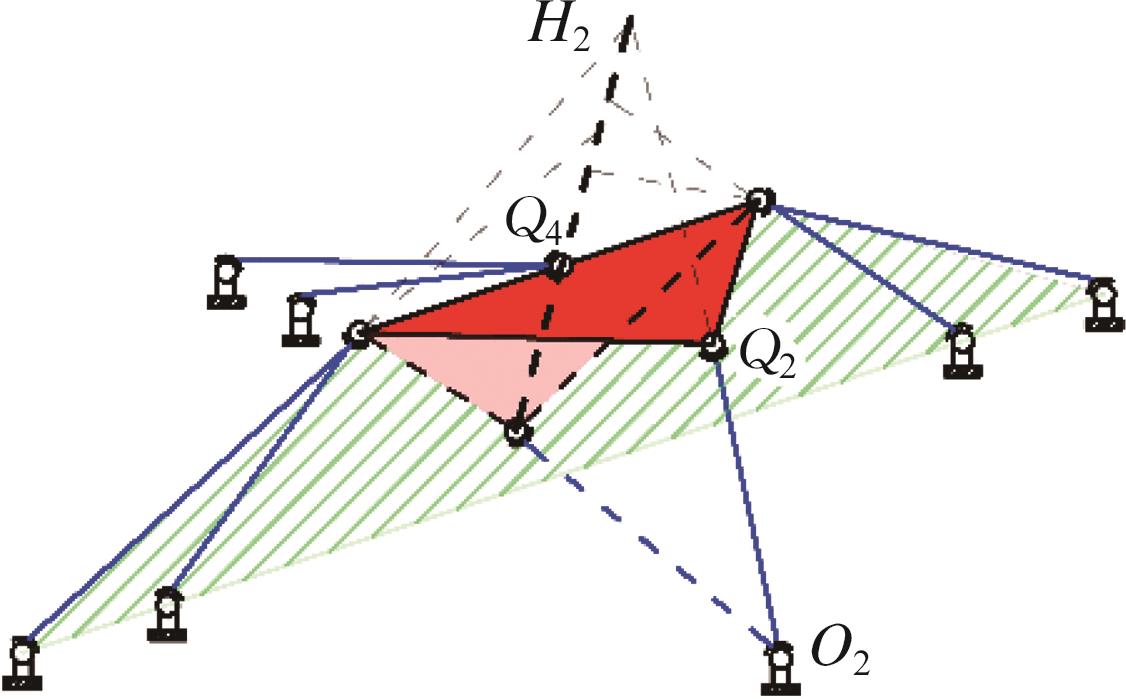 | 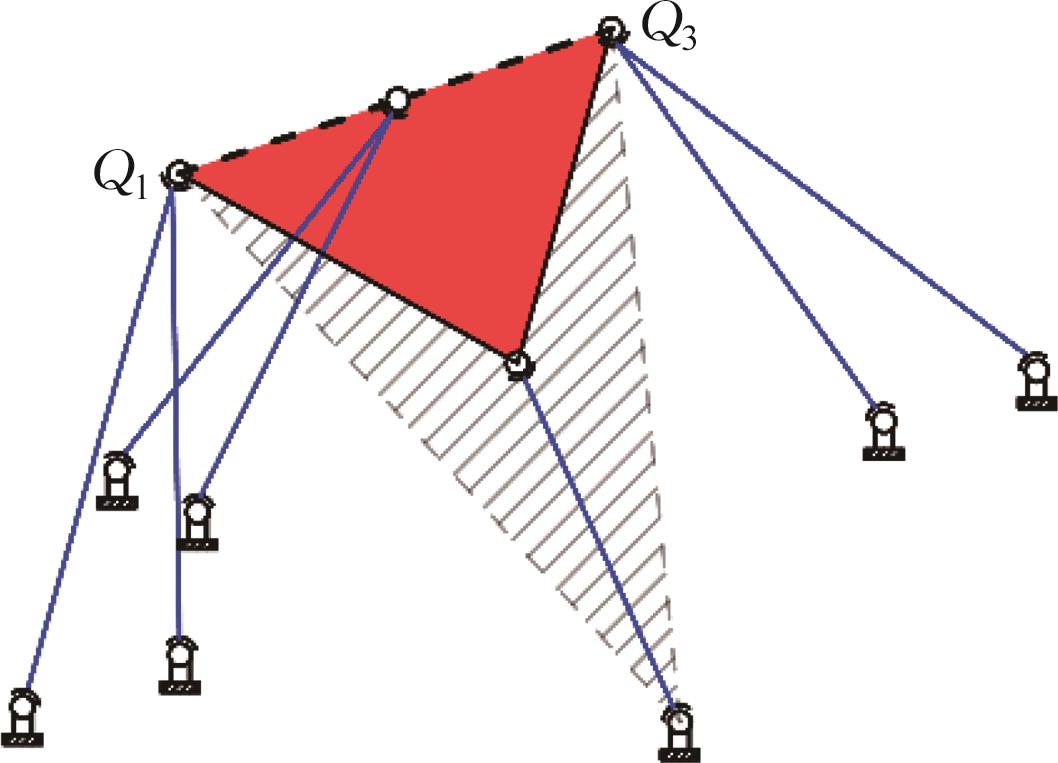 | 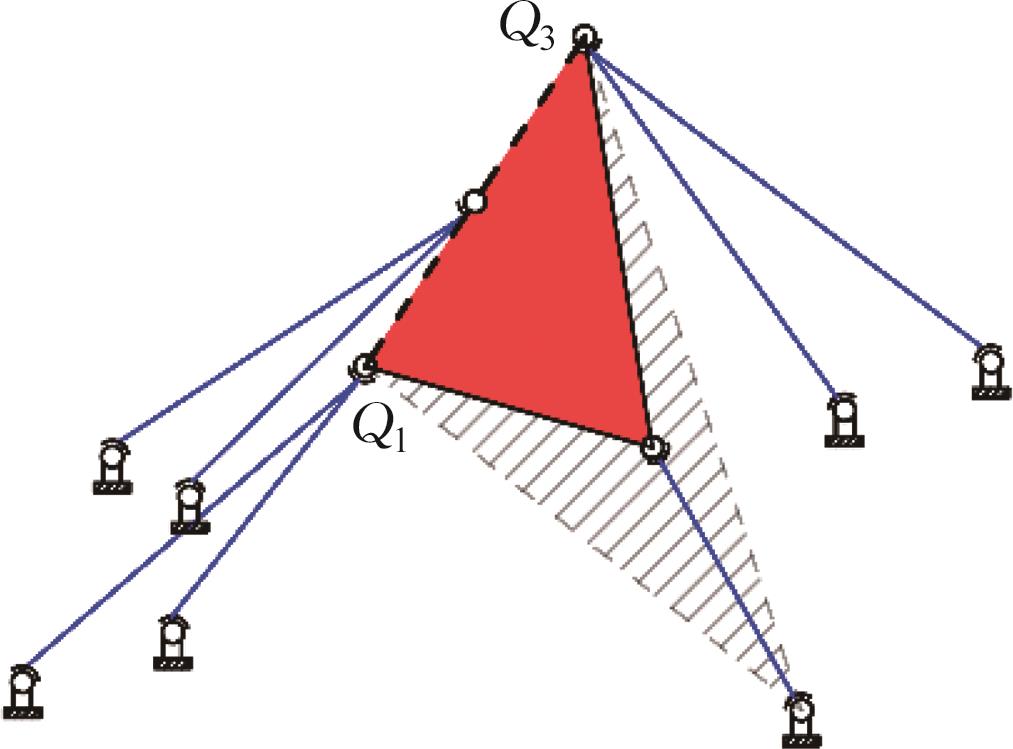 |
| 奇异 | 若O2点位于面H2Q4Q2上,则为Hunt奇异,Q4H2为瞬时旋转轴 | Hunt奇异,Q1Q3为瞬时旋转轴 | |
表6 位置正解个数与奇异性的对应关系
Tab.6 Relationship between the number of forward position solutions and singularity
| 四组位置正解 | 一组位置正解 | ||
|---|---|---|---|
| 构型 |  |  |  |
| 奇异 | 无奇异位形 | Hunt奇异,Q1Q3为瞬时旋转轴 | |
| 两组位置正解 | |||
| 构型 |  |  |  |
| 奇异 | 若O2点位于面H2Q4Q2上,则为Hunt奇异,Q4H2为瞬时旋转轴 | Hunt奇异,Q1Q3为瞬时旋转轴 | |
| [1] | 谢志江, 程清, 丁军, 等. 双支链六自由度并联机构尺度设计与性能分析[J]. 中国机械工程, 2022, 33(14):1680-1690. |
| XIE Zhijiang, CHENG Qing, DING Jun, et al. Dimensional Design and Performance Analysis of a 6-DOF Parallel Manipulator with Two Limbs[J]. China Mechanical Engineering, 2022, 33(14):1680-1690. | |
| [2] | SABATÉ N, ESQUIVEL J P, SANTANDER J, et al. New Approach for Batch Microfabrication of Silicon-based Micro Fuel Cells[J]. Microsystem Technologies, 2014, 20(2):341-348. |
| [3] | YOU Jingjing, XI Fengfeng, SHEN Huiping, et al. A Novel Stewart-type Parallel Mechanism with Topological Reconfiguration:Design, Kinematics and Stiffness Evaluation[J]. Mechanism and Machine Theory, 2021, 162:104329. |
| [4] | 尤晶晶, 符周舟, 吴洪涛, 等. 12-6台体型Stewart冗余并联机构正向运动学研究[J]. 农业机械学报, 2017, 48(12):395-402. |
| YOU Jingjing, FU Zhouzhou, WU Hongtao, et al. Forward Kinematics of General 12-6 Stewart Redundant Parallel Mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(12):395-402. | |
| [5] | ZHOU Wanyong, CHEN Wuyi, LIU Huadong, et al. A New Forward Kinematic Algorithm for a General Stewart Platform[J]. Mechanism and Machine Theory, 2015, 87:177-190. |
| [6] | YANG Xiaolong, WU Hongtao, LI Yao, et al. A Dual Quaternion Solution to the Forward Kinematics of a Class of Six-DOF Parallel Robots with Full or Reductant Actuation[J]. Mechanism and Machine Theory, 2017, 107:27-36. |
| [7] | 沈惠平, 仲锐, 李菊, 等. 运动副分布顺序对并联机构运动学与动力学性能的影响[J]. 农业机械学报, 2023, 54(7):412-426. |
| SHEN Huiping, ZHONG Rui, LI Ju, et al. Influence of Different Distribution Order of Joints on Kinematic and Dynamic Performance of Parallel Mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(7):412-426. | |
| [8] | ZHAO Fuqun, GUO Sheng, ZHANG Chengyu, et al. Singularity Analysis and Dexterity Performance on a Novel Parallel Mechanism with Kinematic Redundancy[J]. International Journal of Advanced Robotic Systems, 2019, 16(5):1729881419872641. |
| [9] | LACOMBE J, GOSSELIN C. Singularity Analysis of a Kinematically Redundant (6+2)-DOF Parallel Mechanism for General Configurations[J]. Mechanism and Machine Theory, 2022, 176:105015. |
| [10] | MONSARRAT B, GOSSELIN C M. Singularity Analysis of a Three-leg Six-degree-of-freedom Parallel Platform Mechanism Based on Grassmann Line Geometry[J]. The International Journal of Robotics Research, 2001, 20(4):312-328. |
| [11] | CHENG Shili, JI Ping. Geometric Algebra Approach to Analyzing the Singularity of Six-DOF Parallel Mechanism[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2019, 13(4):JAMDSM0076. |
| [12] | YANG Tingli, LIU Anxin, SHEN Huiping, et al. On the Correctness and Strictness of the Position and Orientation Characteristic Equation for Topological Structure Design of Robot Mechanisms[J]. Journal of Mechanisms and Robotics, 2013, 5(2):021009. |
| [13] | 沈惠平, 朱小蓉, 尹洪波, 等. 并联机构的结构降耦原理及其设计方法[J]. 机械工程学报, 2016, 52(23):102-113. |
| SHEN Huiping, ZHU Xiaorong, YIN Hongbo, et al. Principle and Design Method for Structure Coupling-reducing of Parallel Mechanisms[J]. Journal of Mechanical Engineering, 2016, 52(23):102-113. | |
| [14] | MA O, ANGELES J. Architecture Singularities of Platform Manipulators[C]∥Proceedings of 1991 IEEE International Conference on Robotics and Automation. Sacramento, 1991:1542-1547. |
| [15] | HUNT K H. Structural Kinematics of In-parallel-Actuated Robot-arms[J]. Journal of Mechanisms, Transmissions, and Automation in Design, 1983, 105(4):705-712. |
| [16] | FICHTER E F. A Stewart-platform Based Manipulator:General Theory and Practical Construction[J]. International Journal of Robotics Research, 1986, 5(2):157-182. |
| [1] | 李明磊, 贾育秦, 张学良, 刘丽琴, 杜娟, 温淑花, 兰国生. 基于多目标差异演化算法的并联机构结构优化 [J]. J4, 201016, 21(16): 1915-1920. |
| [2] | 鲁开讲, 师俊平, 张锋涛. 平面三自由度并联机构动力学优化设计 [J]. J4, 201016, 21(16): 1926-1931. |
| [3] | 李菊, 郭跃, 沈惠平, 孟庆梅, 顾晓阳. 并联机构多重拓扑降耦的优化原理与一般方法[J]. 中国机械工程, 2025, 36(8): 1700-1712. |
| [4] | 赵星宇, 赵铁石, 许博, 刘相权, 秦宇飞. 并联式混合驱动机构运动学和传递性能分析[J]. 中国机械工程, 2025, 36(8): 1728-1739. |
| [5] | 蒲志新, 郭建伟, 潘玉奇, 白杨溪. 2PPaPaR并联机构性能分析及优化设计[J]. 中国机械工程, 2023, 34(19): 2304-2312. |
| [6] | 沈惠平, 李霞, 李菊, 李涛, 孟庆梅, 吴广磊. 约束支链或无约束支链对并联机构运动学与刚度性能的影响——以两个部分运动解耦的新型三平移并联机构的设计、分析及其优选为例[J]. 中国机械工程, 2023, 34(13): 1533-1549. |
| [7] | 杜中秋, 沈惠平, 孟庆梅, 李涛, 杨廷力. 运动解耦且正解符号化的8R两平移空间并联机构的设计与性能分析[J]. 中国机械工程, 2023, 34(12): 1425-1435. |
| [8] | 陈恒通, 王晓光, 江海龙, 林麒. 两种典型六自由度支撑机构大迎角运动特性分析与对比[J]. 中国机械工程, 2023, 34(06): 641-649. |
| [9] | 刘繁茂, 廖灿灿, 张原愿, 莫寒. 新型碟式太阳能聚光器跟踪机构优化设计[J]. 中国机械工程, 2023, 34(04): 395-403. |
| [10] | 董成林, 蔡龙奇, 李毅, 路彤, 张路科. 基于并联机构的三维动力吸振器各向同性设计及减振特性研究[J]. 中国机械工程, 2023, 34(03): 307-313. |
| [11] | 汪满新, 李兰彬, 李正亮, 刘海涛, 黄田. 一类1T2R并联机构拓扑结构综合及优选[J]. 中国机械工程, 2022, 33(20): 2395-2402. |
| [12] | 刘文兰, 于海霞, 瞿怀宇, 马鹏飞, 高小钧, 王建森. 叠加Ⅱ级杆组的正铲液压挖掘机工作机构型综合[J]. 中国机械工程, 2022, 33(16): 1919-1927. |
| [13] | 谢志江, 程清, 丁军, 何苗, 范乃吉, 吴小勇. 双支链六自由度并联机构尺度设计与性能分析[J]. 中国机械工程, 2022, 33(14): 1680-1690. |
| [14] | 王一熙, 沈惠平, 陈谱, 吴广磊. 基于运动学、刚度和动力学性能的并联机构有序递进三级优化设计及其应用[J]. 中国机械工程, 2022, 33(13): 1560-1575,1621. |
| [15] | 朱雅光, 朱建伟, 李茹月, 宋志鹏. 基于神经-肌肉架构的仿生并联躯干柔顺控制[J]. 中国机械工程, 2022, 33(13): 1576-1585,1637. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||