



ISSN 1004-132X
CN 42-1294/TH
CN 42-1294/TH




中国机械工程 ›› 2025, Vol. 36 ›› Issue (11): 2685-2693.DOI: 10.3969/j.issn.1004-132X.2025.11.026
• 智能制造 • 上一篇
收稿日期:2024-06-19
出版日期:2025-11-25
发布日期:2025-12-09
通讯作者:
李好
作者简介:龙千浩,男,2000年生,硕士研究生。研究方向为微结构拓扑优化设计。E-mail:m202270597@hust.edu.cn基金资助:
Qianhao LONG( ), Ying ZHOU, Liang GAO, Hao LI(
), Ying ZHOU, Liang GAO, Hao LI( )
)
Received:2024-06-19
Online:2025-11-25
Published:2025-12-09
Contact:
Hao LI
摘要:
微结构与宏观结构的显著尺度差异,以及复杂的微观几何构型与基材属性的耦合导致微结构的宏观等效性能分析十分困难。提出了一种基于三维卷积神经网络的微结构均质化弹性张量预测模型。采用水平集方法完成微结构的参数化建模,通过数值均质化计算微结构的等效弹性张量。提出几何构型与基材属性耦合的数据表达方法,实现混合输入与等效弹性张量标签的匹配,并将匹配的数据样本作为神经网络训练的数据集。最后,从预测结果的分项误差、计算效率两个方面进行了模型性能分析,所提模型在允许的误差范围内能显著提高微结构的性能分析效率。
中图分类号:
龙千浩, 周颖, 高亮, 李好. 基于三维卷积神经网络的微结构性能快速预测[J]. 中国机械工程, 2025, 36(11): 2685-2693.
Qianhao LONG, Ying ZHOU, Liang GAO, Hao LI. Fast Prediction of Microstructure Performance Based on 3D Convolutional Neural Network[J]. China Mechanical Engineering, 2025, 36(11): 2685-2693.
| 基础单胞 | 二元胞 | 三元胞 | ||
|---|---|---|---|---|
 |  | 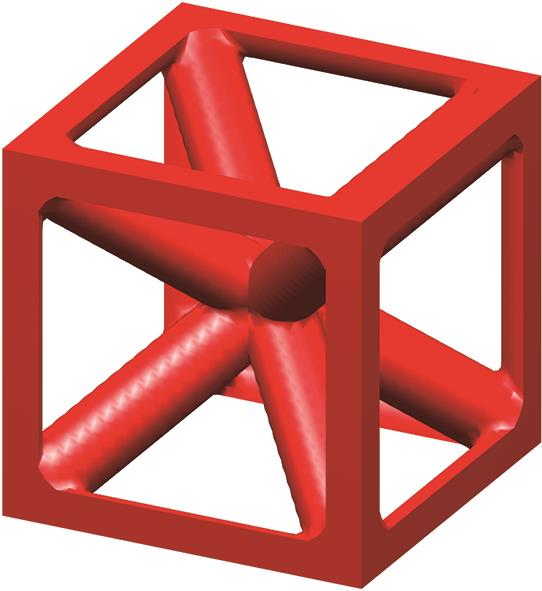 |  |  |
 |  |  |  |  |
 |  | 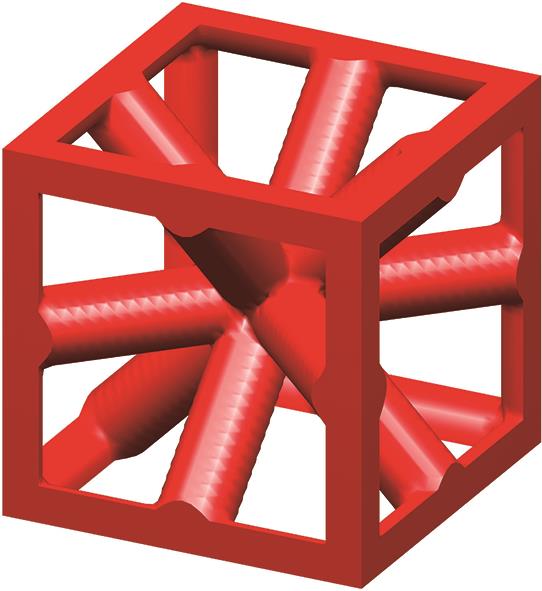 |  |  |
表1 部分训练构型
Tab.1 Partial training configuration
| 基础单胞 | 二元胞 | 三元胞 | ||
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
| 序号 | 结构 | 本层输入、输出的数据维度 |
|---|---|---|
| 1 | 卷积块1 | (2×40×40×40)、(2×20×20×20) |
| 2 | 卷积块2 | (2×20×20×20)、(2×10×10×10) |
| 3 | 卷积块3 | (2×10×10×10)、(2×5×5×5) |
| 4 | 全连接层1 | (2×5×5×5)、128 |
| 5 | 全连接层2 | 128、64 |
| 6 | 全连接层3 | 64、32 |
| 7 | 全连接层4 | 32、3 |
表2 三维卷积神经网络主要构成
Tab.2 Main architecture of 3D convolutional neural network
| 序号 | 结构 | 本层输入、输出的数据维度 |
|---|---|---|
| 1 | 卷积块1 | (2×40×40×40)、(2×20×20×20) |
| 2 | 卷积块2 | (2×20×20×20)、(2×10×10×10) |
| 3 | 卷积块3 | (2×10×10×10)、(2×5×5×5) |
| 4 | 全连接层1 | (2×5×5×5)、128 |
| 5 | 全连接层2 | 128、64 |
| 6 | 全连接层3 | 64、32 |
| 7 | 全连接层4 | 32、3 |
| 微结构 | 体积 分数/ % | 三维卷积网络 预测结果 | 数值均质化 计算结果 | 相对 误差/ % |
|---|---|---|---|---|
 | 11 | (3.99,3.44,3.17) | (4.03,3.45,3.13) | 0.85 |
| 23 | (11.27,8.35,7.48) | (11.18,8.43,7.66) | 1.37 | |
| 35 | (22.15,14.29,13.18) | (22.31,14.14,13.12) | 0.75 | |
| 47 | (40.12,20.98,19.91) | (39.51,20.63,19.73) | 1.38 | |
| 59 | (66.91,28.84,28.22) | (66.22,28.68,27.95) | 0.86 | |
 | 11 | (9.75, 0.76,0.38) | (9.78,0.75,0.39) | 1.40 |
| 23 | (22.19,2.48,1.63) | (22.23,2.41,1.67) | 1.83 | |
| 35 | (38.25,5.63,4.69) | (38.37,5.56,4.76) | 1.01 | |
| 47 | (59.23,11.15.10.49) | (59.34,11.04.10.57) | 0.65 | |
| 59 | (86.28,20.73,19.97) | (87.01,20.45,19.89) | 0.87 | |
 | 11 | (6.26,2.75,2.49) | (6.13,2.84,2.56) | 2.67 |
| 23 | (15.26,6.42,5.78) | (14.93,6.25,5.68) | 2.23 | |
| 35 | (29.25,10.32,10.25) | (28.93,10.65,10.02) | 2.17 | |
| 47 | (48.93,16.12,15.63) | (48.67,15.99,15.55) | 0.62 | |
| 59 | (76.24,23.46,22.71) | (76.62,23.67,23.02) | 0.91 | |
 | 11 | (5.45,3.11,2.94) | (5.37,3.19,2.89) | 1.91 |
| 23 | (13.57,7.47,6.85) | (13.49,7.54,6.78) | 0.85 | |
| 35 | (25.79,12.82,12.25) | (25.78,12.97,11.96) | 1.21 | |
| 47 | (43.85,19.36,18.44) | (43.38,19.08,18.29) | 1.12 | |
| 59 | (71.26,27.65,26.99) | (70.61,27.36,26.82) | 0.87 | |
 | 11 | (6.91,2.56,2.29) | (6.77,2.47,2.22) | 2.95 |
| 23 | (15.88,6.56,5.98) | (15.60,6.46,5.91) | 1.51 | |
| 35 | (28.73,11.35,10.62) | (28.99,11.52,10.84) | 1.47 | |
| 47 | (47.74,18.21,17.35) | (47.19,17.92,17.32) | 1.54 | |
| 59 | (74.63,27.54,26.75) | (74.26,27.22,26.40) | 1.00 |
表3 3D卷积网络预测微结构等效弹性张量的独立参数向量及其相对误差
Tab.3 The independent parameter vectors of the equivalent elastic tensors predicted by the 3D convolutional network and their relative errors
| 微结构 | 体积 分数/ % | 三维卷积网络 预测结果 | 数值均质化 计算结果 | 相对 误差/ % |
|---|---|---|---|---|
 | 11 | (3.99,3.44,3.17) | (4.03,3.45,3.13) | 0.85 |
| 23 | (11.27,8.35,7.48) | (11.18,8.43,7.66) | 1.37 | |
| 35 | (22.15,14.29,13.18) | (22.31,14.14,13.12) | 0.75 | |
| 47 | (40.12,20.98,19.91) | (39.51,20.63,19.73) | 1.38 | |
| 59 | (66.91,28.84,28.22) | (66.22,28.68,27.95) | 0.86 | |
 | 11 | (9.75, 0.76,0.38) | (9.78,0.75,0.39) | 1.40 |
| 23 | (22.19,2.48,1.63) | (22.23,2.41,1.67) | 1.83 | |
| 35 | (38.25,5.63,4.69) | (38.37,5.56,4.76) | 1.01 | |
| 47 | (59.23,11.15.10.49) | (59.34,11.04.10.57) | 0.65 | |
| 59 | (86.28,20.73,19.97) | (87.01,20.45,19.89) | 0.87 | |
 | 11 | (6.26,2.75,2.49) | (6.13,2.84,2.56) | 2.67 |
| 23 | (15.26,6.42,5.78) | (14.93,6.25,5.68) | 2.23 | |
| 35 | (29.25,10.32,10.25) | (28.93,10.65,10.02) | 2.17 | |
| 47 | (48.93,16.12,15.63) | (48.67,15.99,15.55) | 0.62 | |
| 59 | (76.24,23.46,22.71) | (76.62,23.67,23.02) | 0.91 | |
 | 11 | (5.45,3.11,2.94) | (5.37,3.19,2.89) | 1.91 |
| 23 | (13.57,7.47,6.85) | (13.49,7.54,6.78) | 0.85 | |
| 35 | (25.79,12.82,12.25) | (25.78,12.97,11.96) | 1.21 | |
| 47 | (43.85,19.36,18.44) | (43.38,19.08,18.29) | 1.12 | |
| 59 | (71.26,27.65,26.99) | (70.61,27.36,26.82) | 0.87 | |
 | 11 | (6.91,2.56,2.29) | (6.77,2.47,2.22) | 2.95 |
| 23 | (15.88,6.56,5.98) | (15.60,6.46,5.91) | 1.51 | |
| 35 | (28.73,11.35,10.62) | (28.99,11.52,10.84) | 1.47 | |
| 47 | (47.74,18.21,17.35) | (47.19,17.92,17.32) | 1.54 | |
| 59 | (74.63,27.54,26.75) | (74.26,27.22,26.40) | 1.00 |
| 训练构型 | 神经网络预测结果 | 数值均值化结果 | ||
|---|---|---|---|---|
| 弹性模量 | 剪切模量 | 弹性模量 | 剪切模量 | |
 |
Emax=4.37 GPa, Emin=0.69 GPa |
Gmax=1.87 GPa, Gmin=0.33 GPa |
Emax=4.43 GPa, Emin=0.72 GPa |
Gmax=1.89 GPa, Gmin=0.35 GPa |
 |
Emax=5.77 GPa, Emin=5.53 GPa |
Gmax=2.29 GPa, Gmin=2.21 GPa |
Emax=5.60 GPa, Emin=6.45 GPa |
Gmax=2.22 GPa, Gmin=2.17 GPa |
 |
Emax=18.29 GPa, Emin=8.71 GPa |
Gmax=7.58 GPa, Gmin=3.96 GPa |
Emax=18.45 GPa, Emin=8.78 GPa |
Gmax=7.65 GPa, Gmin=4.00 GPa |
 |
Emax=12.14 GPa, Emin=11.44 GPa |
Gmax=4.73 GPa, Gmin=4.52 GPa |
Emax=12.21 GPa, Emin=11.74 GPa |
Gmax=4.80 GPa, Gmin=4.65 GPa |
表4 卷积神经网络和数值均匀化方法所得力学画像
Tab.4 Mechanical images of convolution network and numerical homogenization calculation results
| 训练构型 | 神经网络预测结果 | 数值均值化结果 | ||
|---|---|---|---|---|
| 弹性模量 | 剪切模量 | 弹性模量 | 剪切模量 | |
 |
Emax=4.37 GPa, Emin=0.69 GPa |
Gmax=1.87 GPa, Gmin=0.33 GPa |
Emax=4.43 GPa, Emin=0.72 GPa |
Gmax=1.89 GPa, Gmin=0.35 GPa |
 |
Emax=5.77 GPa, Emin=5.53 GPa |
Gmax=2.29 GPa, Gmin=2.21 GPa |
Emax=5.60 GPa, Emin=6.45 GPa |
Gmax=2.22 GPa, Gmin=2.17 GPa |
 |
Emax=18.29 GPa, Emin=8.71 GPa |
Gmax=7.58 GPa, Gmin=3.96 GPa |
Emax=18.45 GPa, Emin=8.78 GPa |
Gmax=7.65 GPa, Gmin=4.00 GPa |
 |
Emax=12.14 GPa, Emin=11.44 GPa |
Gmax=4.73 GPa, Gmin=4.52 GPa |
Emax=12.21 GPa, Emin=11.74 GPa |
Gmax=4.80 GPa, Gmin=4.65 GPa |
| 数值均质化方法 | 三维卷积神经网络 | |
|---|---|---|
| 总耗时 | 3445.6 | 2.1 |
| 单个耗时 | 34.46 | 0.02 |
表5 100个微结构的计算耗时 (s)
Tab.5 Consuming time in calculation of 100 microstructures
| 数值均质化方法 | 三维卷积神经网络 | |
|---|---|---|
| 总耗时 | 3445.6 | 2.1 |
| 单个耗时 | 34.46 | 0.02 |
| 训练构型 | 神经网络预测结果 | 数值均值化结果 | ||
|---|---|---|---|---|
| 弹性模量 | 剪切模量 | 弹性模量 | 剪切模量 | |
 |
Emax=3.80 GPa, Emin=0.46 GPa |
Gmax=0.54 GPa, Gmin=0.16 GPa |
Emax=3.83 GPa, Emin=0.49 GPa |
Gmax=0.55 GPa, Gmin=0.17 GPa |
 |
Emax=2.37 GPa, Emin=1.64 GPa |
Gmax=0.96 GPa, Gmin=0.71 GPa |
Emax=2.44 GPa, Emin=1.65 GPa |
Gmax=0.99 GPa, Gmin=0.717 GPa |
表6 测试对象的力学画像
Tab.6 Mechanical images of test subjects
| 训练构型 | 神经网络预测结果 | 数值均值化结果 | ||
|---|---|---|---|---|
| 弹性模量 | 剪切模量 | 弹性模量 | 剪切模量 | |
 |
Emax=3.80 GPa, Emin=0.46 GPa |
Gmax=0.54 GPa, Gmin=0.16 GPa |
Emax=3.83 GPa, Emin=0.49 GPa |
Gmax=0.55 GPa, Gmin=0.17 GPa |
 |
Emax=2.37 GPa, Emin=1.64 GPa |
Gmax=0.96 GPa, Gmin=0.71 GPa |
Emax=2.44 GPa, Emin=1.65 GPa |
Gmax=0.99 GPa, Gmin=0.717 GPa |
| [1] | 卢天健, 何德坪, 陈常青, 等. 超轻多孔金属材料的多功能特性及应用[J]. 力学进展, 2006, 36(4): 517-535. |
| LU Tianjian, HE Deping, CHEN Changqing, et al. The Multi-functionality of Ultra-light Porous Metals and Their Applications[J]. Advances in Mechanics, 2006, 36(4): 517-535. | |
| [2] | 熊健, 杜昀桐, 杨雯, 等. 轻质复合材料夹芯结构设计及力学性能最新进展[J]. 宇航学报, 2020, 41(6): 749-760. |
| XIONG Jian, DU Yuntong, YANG Wen, et al. Research Progress on Design and Mechanical Properties of Lightweight Composite Sandwich Structures[J]. Journal of Astronautics, 2020, 41(6): 749-760. | |
| [3] | 雷红帅, 赵则昂, 郭晓岗, 等. 航天器轻量化多功能结构设计与制造技术研究进展[J]. 宇航材料工艺, 2021, 51(4): 10-22. |
| LEI Hongshuai, ZHAO Zeang, GUO Xiaogang, et al. Research Progress on the Design and Manufacture Technology of Lightweight Multifunctional Spacecraft Structures[J]. Aerospace Materials & Technology, 2021, 51(4): 10-22. | |
| [4] | SAEB S, STEINMANN P, JAVILI A. Aspects of Computational Homogenization at Finite Deformations: a Unifying Review from Reuss' to Voigt's Bound[J]. Applied Mechanics Reviews, 2016, 68(5): 050801. |
| [5] | HASHIN Z, SHTRIKMAN S. A Variational Approach to the Theory of the Effective Magnetic Permeability of Multiphase Materials[J]. Journal of Applied Physics, 1962, 33(10): 3125-3131. |
| [6] | MORI T, TANAKA K. Average Stress in Matrix and Average Elastic Energy of Materials with Misfitting Inclusions[J]. Acta Metallurgica, 1973, 21(5): 571-574. |
| [7] | BENVENISTE Y. A New Approach to the Application of Mori-Tanaka's Theory in Composite Materials[J]. Mechanics of Materials, 1987, 6(2): 147-157. |
| [8] | KRÖNER E. Berechnung Der Elastischen Konstanten des Vielkristalls Aus Den Konstanten des Einkristalls[J]. Zeitschrift Für Physik, 1958, 151(4): 504-518. |
| [9] | WILLIS J R. Bounds and Self-consistent Estimates for the Overall Properties of Anisotropic Composites[J]. Journal of the Mechanics and Physics of Solids, 1977, 25(3): 185-202. |
| [10] | KERNER E H. The Elastic and Thermo-elastic Properties of Composite Media[J]. Proceedings of the Physical Society Section B, 1956, 69(8): 808-813. |
| [11] | CHATZIGEORGIOU G, SEIDEL G D, LAGOUDAS D C. Effective Mechanical Properties of “Fuzzy Fiber” Composites[J]. Composites Part B: Engineering, 2012, 43(6): 2577-2593. |
| [12] | 蔡园武. 周期性板结构的渐近均匀化方法及微结构优化[D]. 大连: 大连理工大学, 2014. |
| CAI Yuanwu. Asymptotic Homogenization of Periodic Plate and Micro-structural Optimization[D]. Dalian: Dalian University of Technology, 2014. | |
| [13] | HASSANI B, HINTON E. A Review of Homogenization and Topology Optimization I—Homogenization Theory for Media with Periodic Structure[J]. Computers & Structures, 1998, 69(6): 707-717. |
| [14] | 张永存, 尚士朋, 梁宇静. 周期性复合材料等效传热系数预测的渐进均匀化新算法及其实现[J]. 复合材料学报, 2018, 35(1): 208-217. |
| ZHANG Yongcun, SHANG Shipeng, LIANG Yujing. A New Algorithm of Asymptotic Homogenization Method for Predicting the Effective Thermal Conductivity and Its Implementation of Periodic Composite Materials[J]. Acta Materiae Compositae Sinica, 2018, 35(1): 208-217. | |
| [15] | SCHUMACHER C, BICKEL B, RYS J, et al. Microstructures to Control Elasticity in 3D Printing[J]. ACM Transactions on Graphics, 2015, 34(4): 1-13. |
| [16] | PANETTA J, ZHOU Qingnan, MALOMO L, et al. Elastic Textures for Additive Fabrication[J]. ACM Transactions on Graphics, 2015, 34(4): 1-12. |
| [17] | MARTÍNEZ J, DUMAS J, LEFEBVRE S. Procedural Voronoi Foams for Additive Manufacturing[J]. ACM Transactions on Graphics, 2016, 35(4): 1-12. |
| [18] | TEMIZER İ, WRIGGERS P. An Adaptive Method for Homogenization in Orthotropic Nonlinear Elasticity[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(35/36): 3409-3423. |
| [19] | YVONNET J, GONZALEZ D, HE Q C. Numerically Explicit Potentials for the Homogenization of Nonlinear Elastic Heterogeneous Materials[J]. Computer Methods in Applied Mechanics and Engineering, 2009, 198(33/36): 2723-2737. |
| [20] | YVONNET J, MONTEIRO E, HE Qichang. Computational Homogenization Method and Reduced Database Model for Hyperelastic Heterogeneous Structures[J]. International Journal for Multiscale Computational Engineering, 2013, 11(3): 201-225. |
| [21] | LIU Peiqing, LIU An, PENG Hao, et al. Mechanical Property Profiles of Microstructures via Asymptotic Homogenization[J]. Computers & Graphics, 2021, 100: 106-115. |
| [22] | FRITZEN F, KUNC O. Two-stage Data-driven Homogenization for Nonlinear Solids Using a Reduced Order Model[J]. European Journal of Mechanics—A/Solids, 2018, 69: 201-220. |
| [23] | LE B A, YVONNET J, HE Q C. Computational Homogenization of Nonlinear Elastic Materials Using Neural Networks[J]. International Journal for Numerical Methods in Engineering, 2015, 104(12): 1061-1084. |
| [24] | LU Xiaoxin, GIOVANIS D G, YVONNET J, et al. A Data-driven Computational Homogenization Method Based on Neural Networks for the Nonlinear Anisotropic Electrical Response of Graphene/Polymer Nanocomposites[J]. Computational Mechanics, 2019, 64(2): 307-321. |
| [25] | BERMEJILLO BARRERA M D, FRANCO-MARTÍNEZ F, DÍAZ LANTADA A. Artificial Intelligence Aided Design of Tissue Engineering Scaffolds Employing Virtual Tomography and 3D Convolutional Neural Networks[J]. Materials, 2021, 14(18): 5278. |
| [26] | WU Peichen, IQUEBAL A S, ANKIT K. Emulating Microstructural Evolution during Spinodal Decomposition Using a Tensor Decomposed Convolutional and Recurrent Neural Network[J]. Computational Materials Science, 2023, 224: 112187. |
| [27] | ZHENG Li, KUMAR S, KOCHMANN D M. Data-driven Topology Optimization of Spinodoid Metamaterials with Seamlessly Tunable Anisotropy[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 383: 113894. |
| [28] | ZHENG Xiaoyang, CHEN Tate, GUO Xiaofeng, et al. Controllable Inverse Design of Auxetic Metamaterials Using Deep Learning[J]. Materials & Design, 2021, 211: 110178. |
| [29] | DONG Jiaqi, QIN Qinghua, XIAO Yi. Nelder-mead Optimization of Elastic Metamaterials via Machine-learning-aided Surrogate Modeling[J]. International Journal of Applied Mechanics, 2020, 12(1): 2050011. |
| [30] | ANDREASSEN E, ANDREASEN C S. How to Determine Composite Material Properties Using Numerical Homogenization[J]. Computational Materials Science, 2014, 83: 488-495. |
| [1] | 李小力, 陈威, 闫蓉. 基于BP神经网络的空间轮廓误差自适应补偿 [J]. J4, 201016, 21(16): 1902-1906. |
| [2] | 赵伟, 王志远, 周志立. 载重汽车连续下坡弯道路段制动稳定性仿真研究 [J]. J4, 201016, 21(16): 2010-2015. |
| [3] | 王坚坚, 廖与禾, 杨磊, 薛久涛. 基于多维复向特征融合与CNN-GRU的转子不平衡量识别方法[J]. 中国机械工程, 2025, 36(9): 1905-1915. |
| [4] | 徐宏伟, 叶文斌, 马顺尧, 张航. FDM全彩色3D打印机颜色匹配标定算法研究[J]. 中国机械工程, 2025, 36(9): 2081-2086. |
| [5] | 邢海燕, 武雪缘, 蔡智会, 赵力伟, 苏田, 韩晴. 基于ResGNNet多模态融合的油气管道缺陷等级磁记忆定量识别[J]. 中国机械工程, 2025, 36(9): 2150-2157. |
| [6] | 岳子桐, 李艳婷, 赵宇. 基于神经网络和稳健估计的风电机组状态监测[J]. 中国机械工程, 2025, 36(8): 1842-1852. |
| [7] | 陈智博, 李国平, 项四通, 魏燕定. 基于超声谐振挤压膜效应的触觉纹理动态感知及实验研究[J]. 中国机械工程, 2025, 36(11): 2574-2582. |
| [8] | 董佳祥, 刘铨权, 胡希平, 赵学智. 新型刚柔混联连续体机器人运动建模[J]. 中国机械工程, 2025, 36(11): 2678-2684. |
| [9] | 陈晶晶, 陈莎, 朱海燕, 袁军军, 罗泽宇. SiC硬脆材料纳米切削的亚表层损伤与塑性去除机理探析[J]. 中国机械工程, 2025, 36(10): 2312-2321. |
| [10] | 倪敬1, 卢蝶1, 蒙臻1, 林少荣1, 王阳1, 傅云2. 激光创成微结构几何精度与润湿性能的关联机制[J]. 中国机械工程, 2025, 36(07): 1423-1429,1561. |
| [11] | 杨赫然1, 2, 张培杰1, 2, 孙兴伟1, 2, 潘飞1, 2, 刘寅1, 2. 利用改进卷积神经网络的螺杆砂带磨削表面粗糙度预测[J]. 中国机械工程, 2025, 36(02): 325-332. |
| [12] | 郭海宇1, 邹圣公1, 张晓光2, 3, 4, 陆凡凡2, 陈洋2, 王涵2, 徐新志2. 基于多源小波变换神经网络的旋转机械轴承故障诊断[J]. 中国机械工程, 2024, 35(11): 2026-2034. |
| [13] | 吴蒙华1, 姜炳春1, 肖雨晴2, 贾卫平2. 磁场对无掩模定域性电沉积增材制造三维微结构生长模式的影响[J]. 中国机械工程, 2024, 35(11): 2035-2042. |
| [14] | 聂鹏1, 杨程越1, 彭新月1, 于家鹤2, 潘五九1. 采用空间和通道激励注意力机制优化ResNet-50的CFRP/TC4叠层材料钻削刀具磨损状态监测[J]. 中国机械工程, 2024, 35(10): 1793-1801. |
| [15] | 张文华1, 尹文良1, 张祯滨2, 刘琳3, 彭克1. 计及叶轮不平衡的差动调速风电机组变桨距控制[J]. 中国机械工程, 2024, 35(10): 1890-1899. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||