



ISSN 1004-132X
CN 42-1294/TH
CN 42-1294/TH




中国机械工程 ›› 2025, Vol. 36 ›› Issue (11): 2609-2617.DOI: 10.3969/j.issn.1004-132X.2025.11.016
• 机械基础工程 • 上一篇
李想1,2( ), 刘焕牢1,2(
), 刘焕牢1,2( ), 王宇林1,2, 戴鑫1,2
), 王宇林1,2, 戴鑫1,2
收稿日期:2024-11-12
出版日期:2025-11-25
发布日期:2025-12-09
通讯作者:
刘焕牢
作者简介:李想,男,1999年生,硕士研究生。研究方向为数控装备技术及其动力学。E-mail:lixiangbean@163.com基金资助:
Xiang LI1,2( ), Huanlao LIU1,2(
), Huanlao LIU1,2( ), Yulin WANG1,2, Xin DAI1,2
), Yulin WANG1,2, Xin DAI1,2
Received:2024-11-12
Online:2025-11-25
Published:2025-12-09
Contact:
Huanlao LIU
摘要:
为快速辨识五轴机床旋转轴位置无关几何误差(PIGEs),提高旋转轴几何误差辨识精度,提出了一种采用三种球杆仪安装模式的旋转轴PIGEs简便辨识方法。在三种球杆仪安装模式下,通过齐次坐标变换建立了包含安装误差与旋转轴PIGEs的杆长变化模型。利用仿真分析了PIGEs对三种安装模式下球杆仪轨迹的影响,结果表明三种安装模式下控制单轴运动可以实现8项PIGEs的辨识。在辨识实验中,通过对球杆仪安装误差的测量来消除其对辨识精度的影响,以实现旋转轴8项PIGEs的辨识。最后对旋转轴8项PIGEs进行了补偿,实验结果表明,补偿后的误差最大绝对值由103.9 μm减小至 0.46 μm,验证了所提辨识方法的有效性和准确性。
中图分类号:
李想, 刘焕牢, 王宇林, 戴鑫. 一种五轴机床旋转轴位置无关几何误差辨识方法[J]. 中国机械工程, 2025, 36(11): 2609-2617.
Xiang LI, Huanlao LIU, Yulin WANG, Xin DAI. An Identification Method of PIGEs for Rotary Axes of Five-axis Machine Tools[J]. China Mechanical Engineering, 2025, 36(11): 2609-2617.
| 参数 | 数值 |
|---|---|
| 球杆仪标称长度L/mm | 100 |
| 工件球球心相对于刀具球球心在X方向上的偏移量LX /mm | 60 |
| 工件球球心相对于刀具球球心在Y方向上的偏移量LY /mm | 80 |
| 刀具球球心到C轴轴线的距离l/mm | 100 |
| 刀具球球心到A轴轴线的距离h/mm | 100 |
| A轴旋转范围 | [-15°,70°] |
| C轴旋转范围 | [0°,360°] |
| ACS与CCS间的距离ZAC /mm | 50 |
| 位置误差δYA,δZA,δXC,δYC /μm | ±10 |
| 垂直度误差SYA,SZA,SXC,SYC /(°) | ±0.005 |
表1 仿真基本参数
Tab.1 Basic parameters of simulation
| 参数 | 数值 |
|---|---|
| 球杆仪标称长度L/mm | 100 |
| 工件球球心相对于刀具球球心在X方向上的偏移量LX /mm | 60 |
| 工件球球心相对于刀具球球心在Y方向上的偏移量LY /mm | 80 |
| 刀具球球心到C轴轴线的距离l/mm | 100 |
| 刀具球球心到A轴轴线的距离h/mm | 100 |
| A轴旋转范围 | [-15°,70°] |
| C轴旋转范围 | [0°,360°] |
| ACS与CCS间的距离ZAC /mm | 50 |
| 位置误差δYA,δZA,δXC,δYC /μm | ±10 |
| 垂直度误差SYA,SZA,SXC,SYC /(°) | ±0.005 |
| 误差 | ||||
|---|---|---|---|---|
模式一 仅A轴 旋转 | 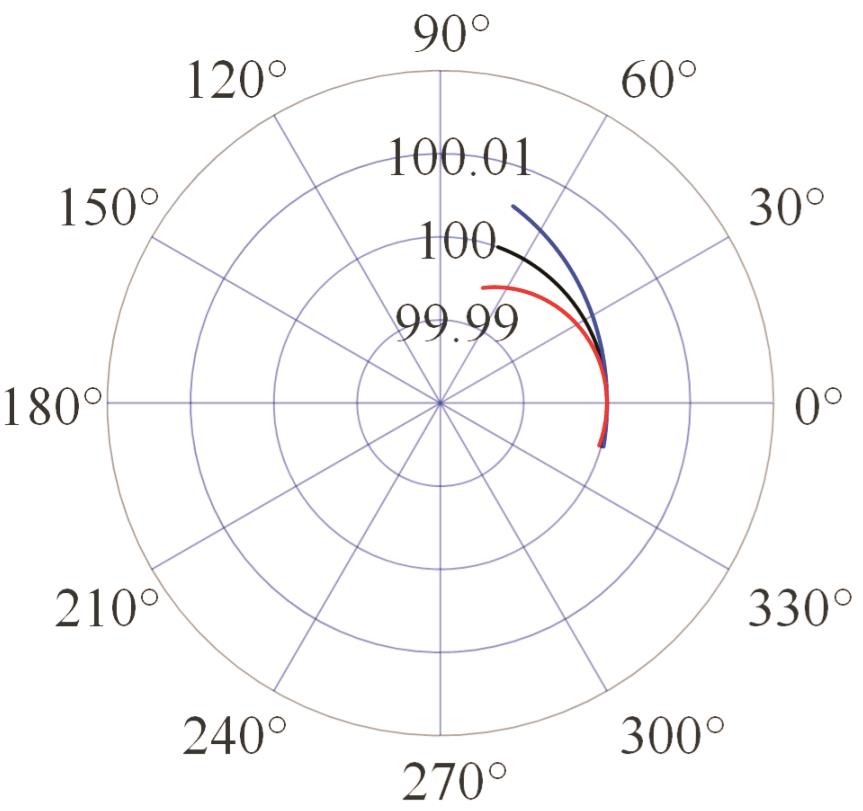 | 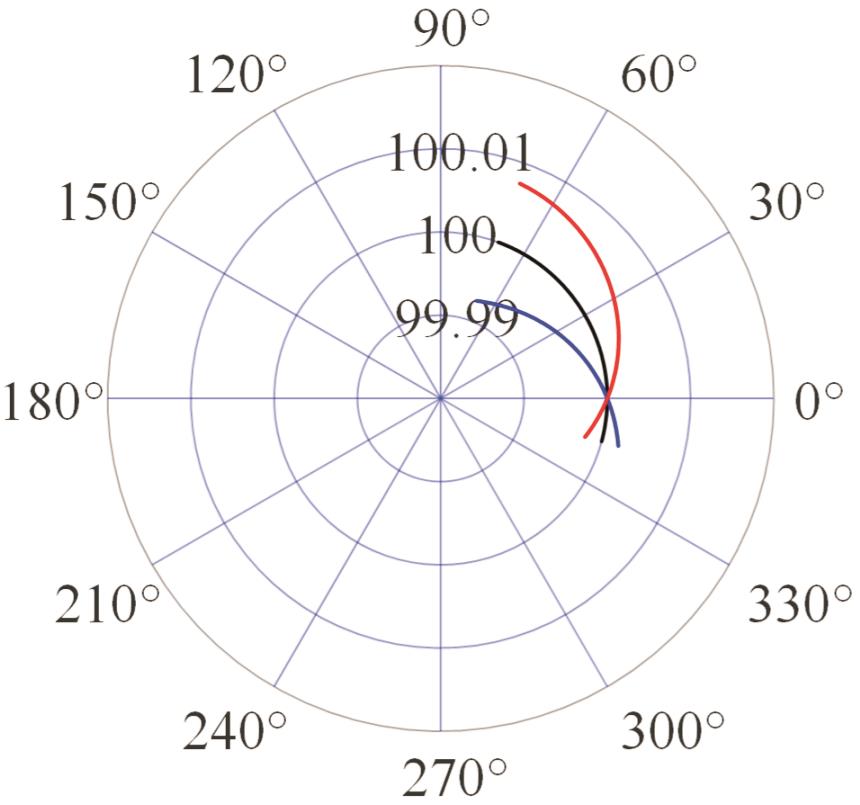 | 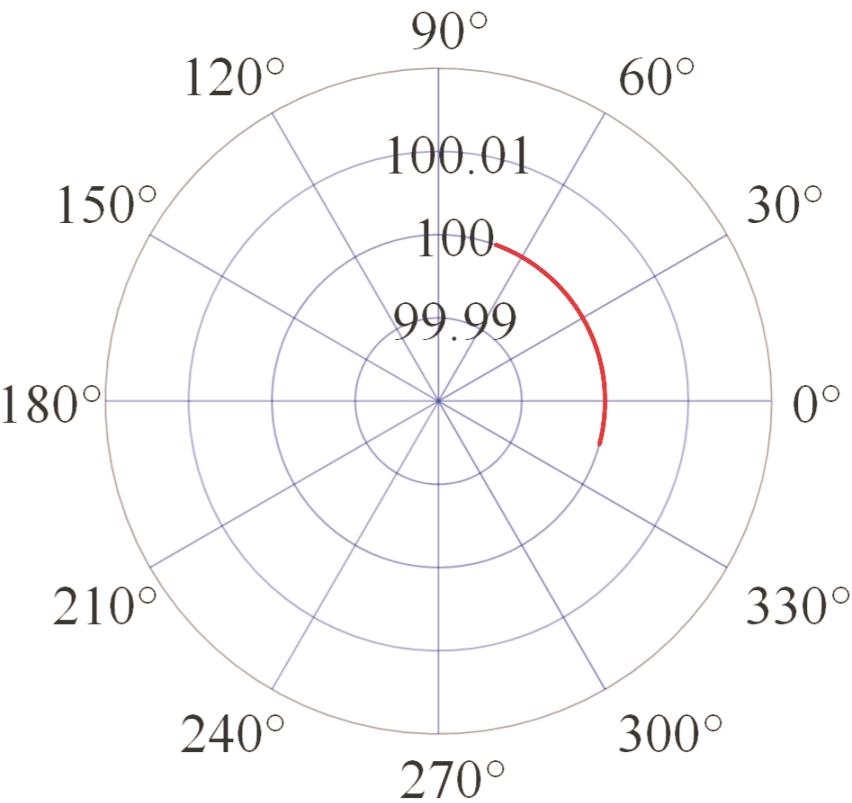 | 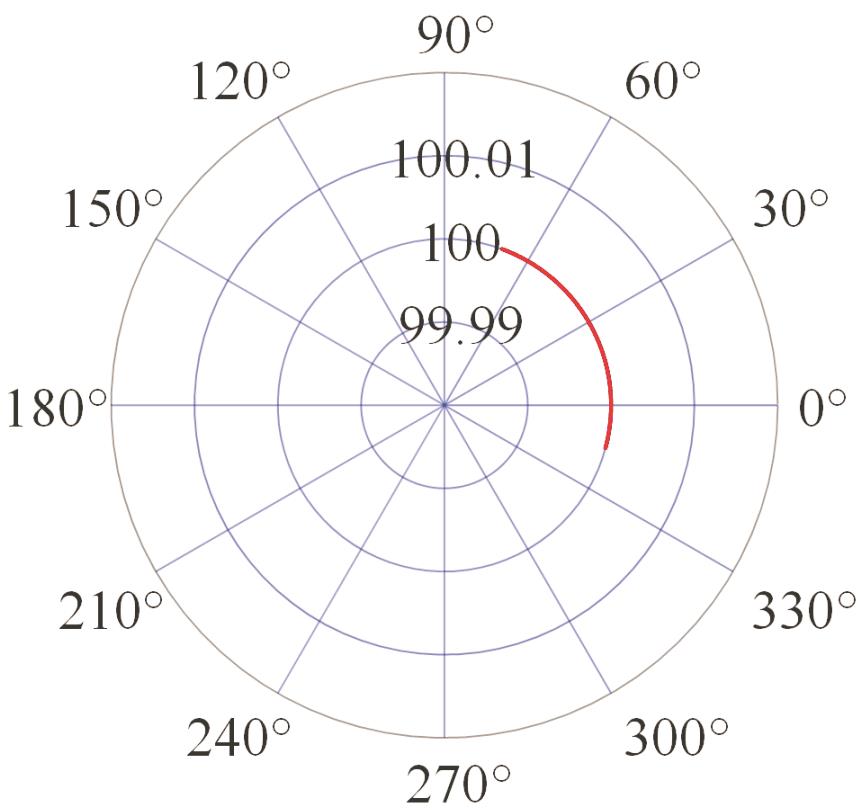 |
| 模式二 | 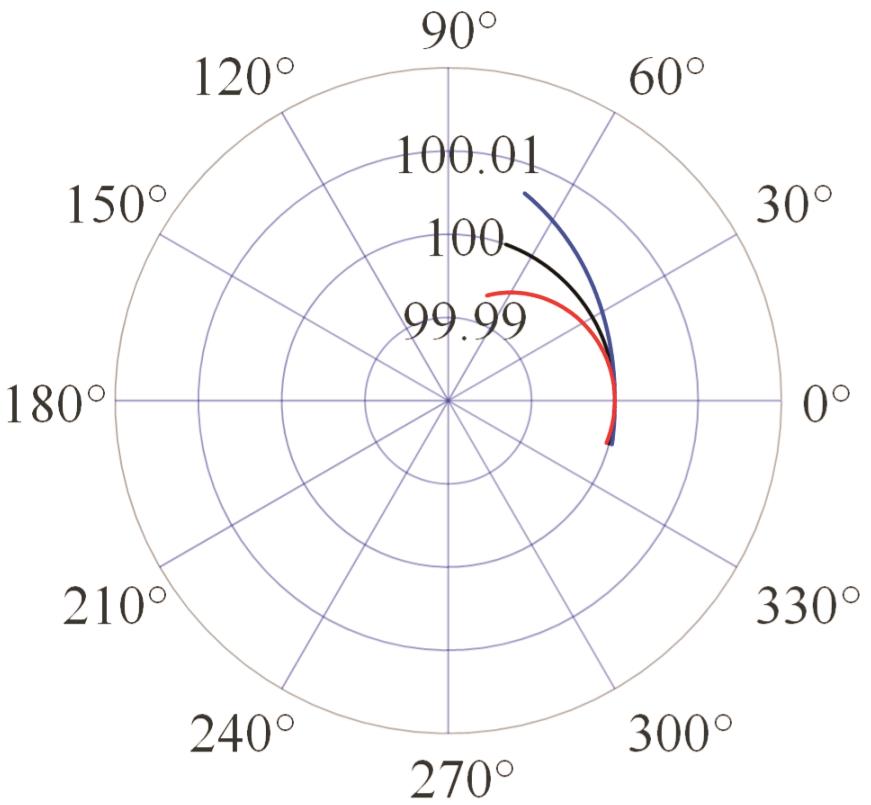 | 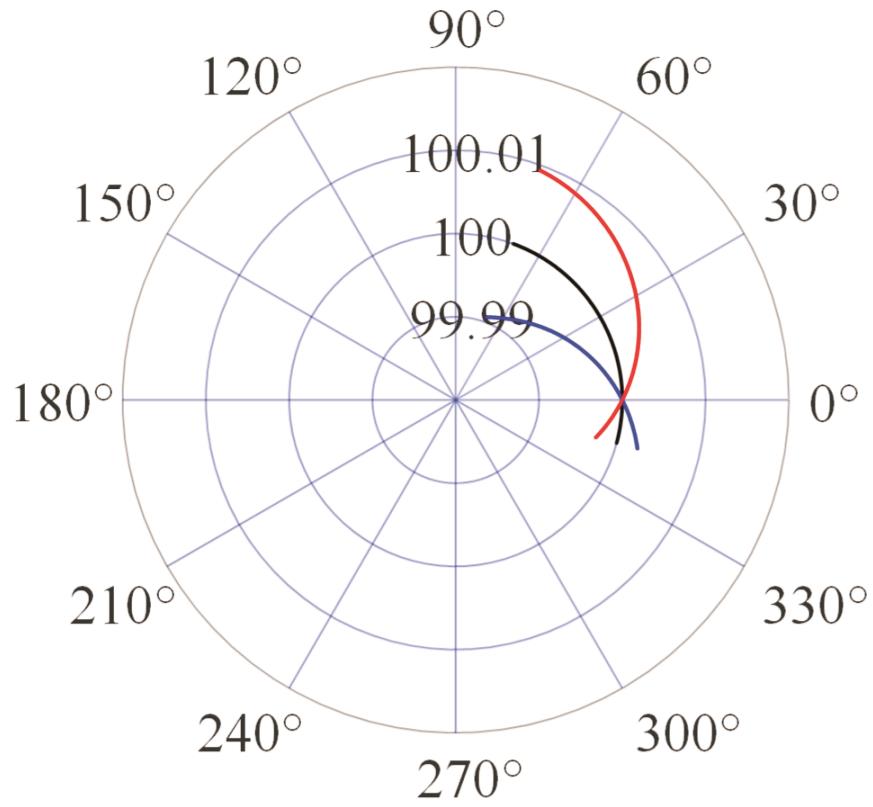 | 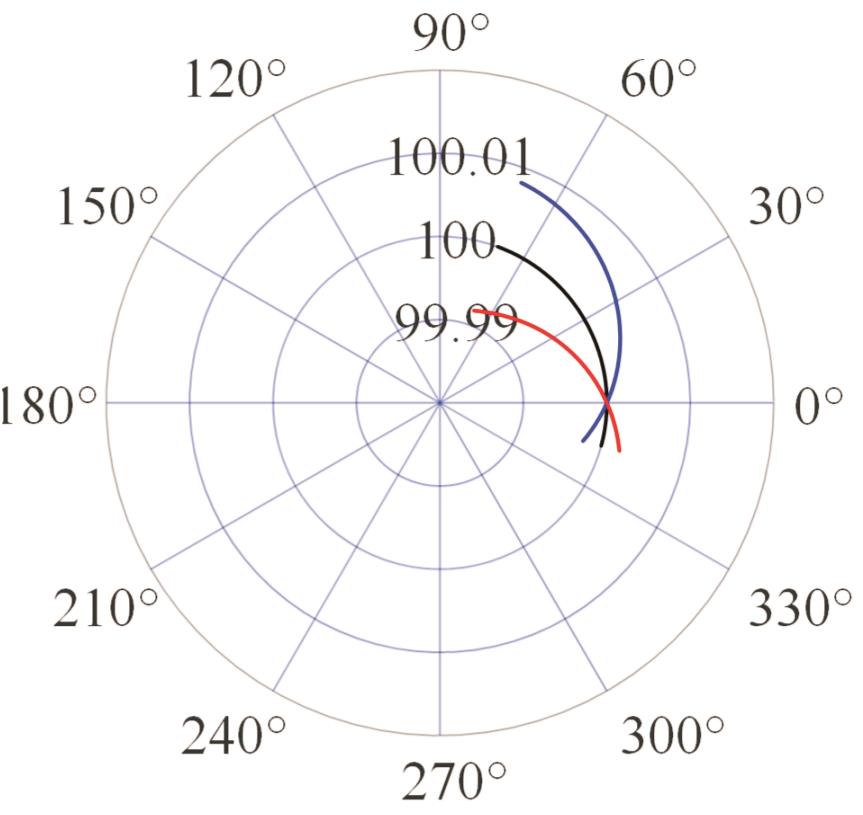 | 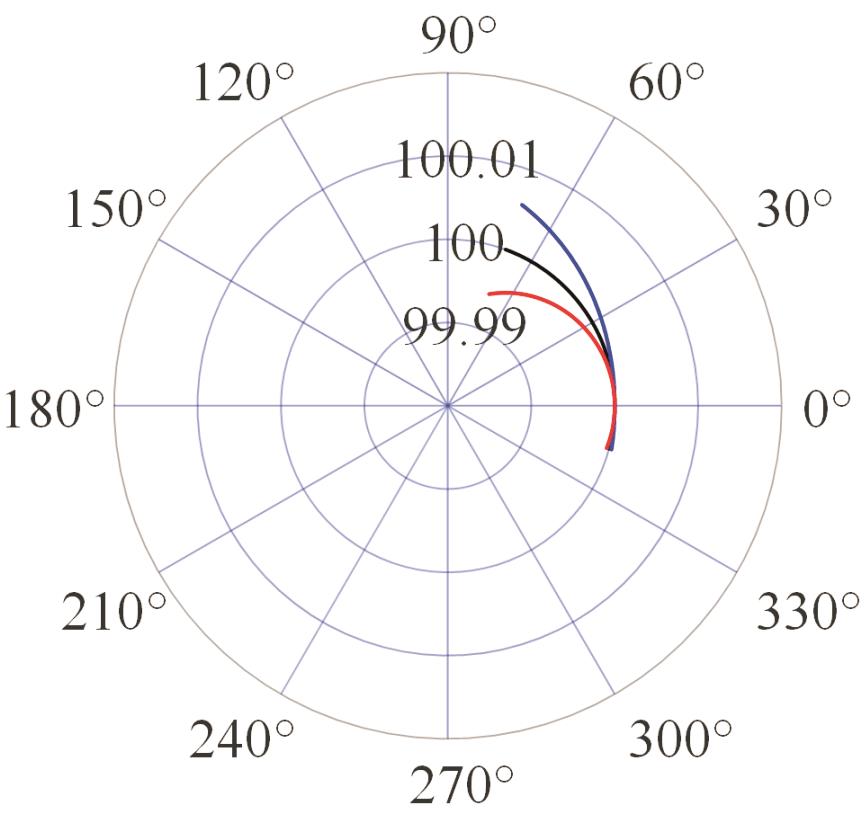 |
模式一 仅C轴 旋转 | 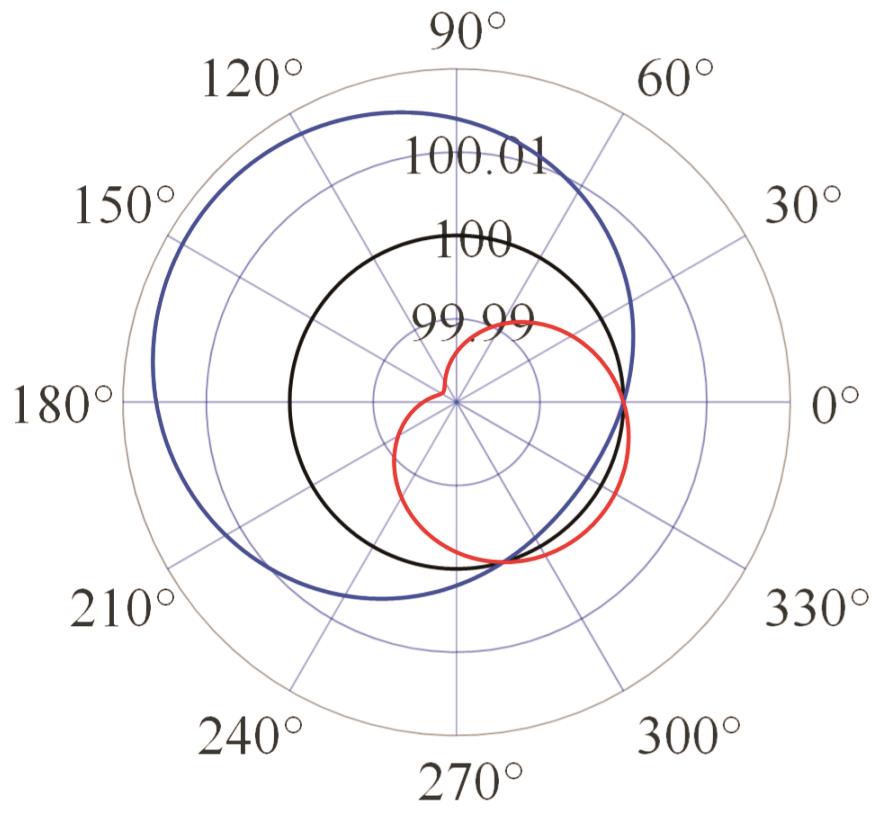 | 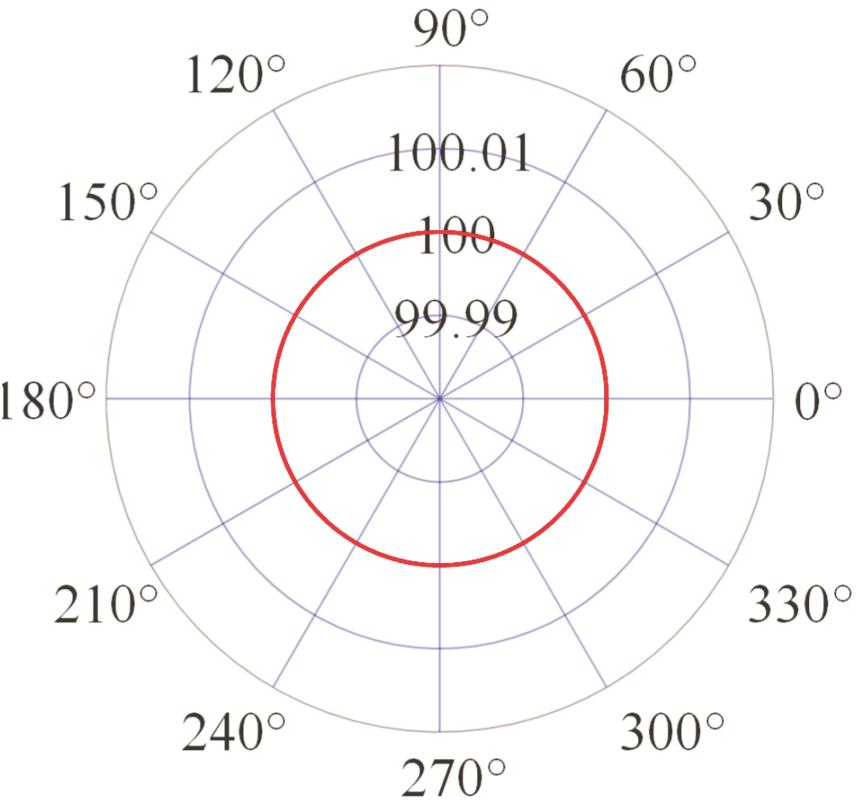 | ||
| 模式三 | 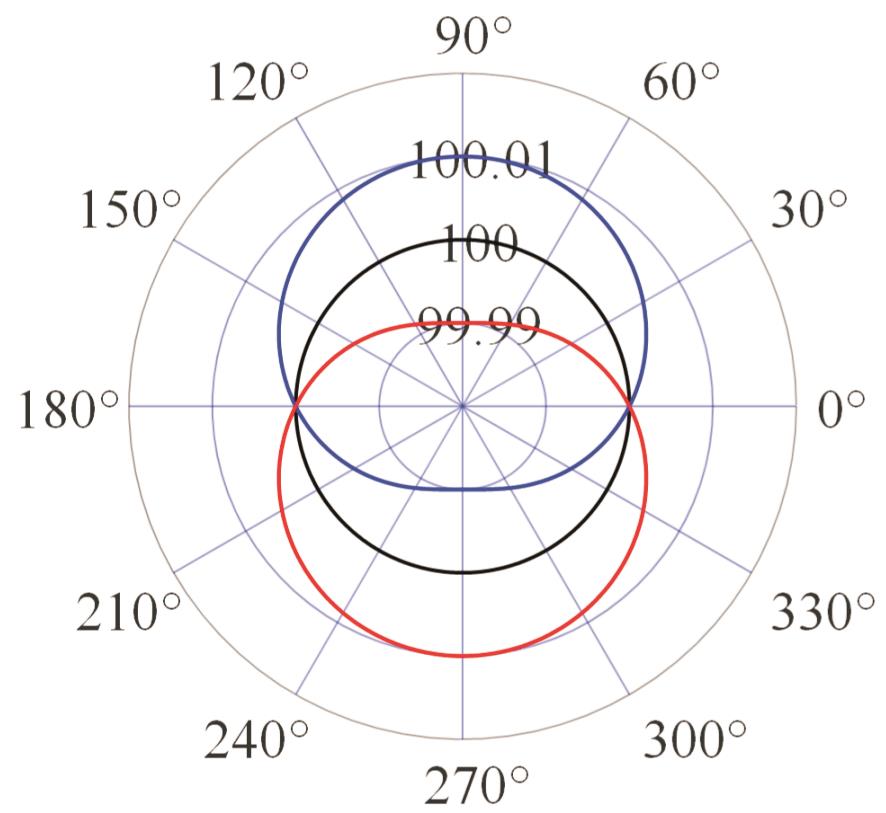 | 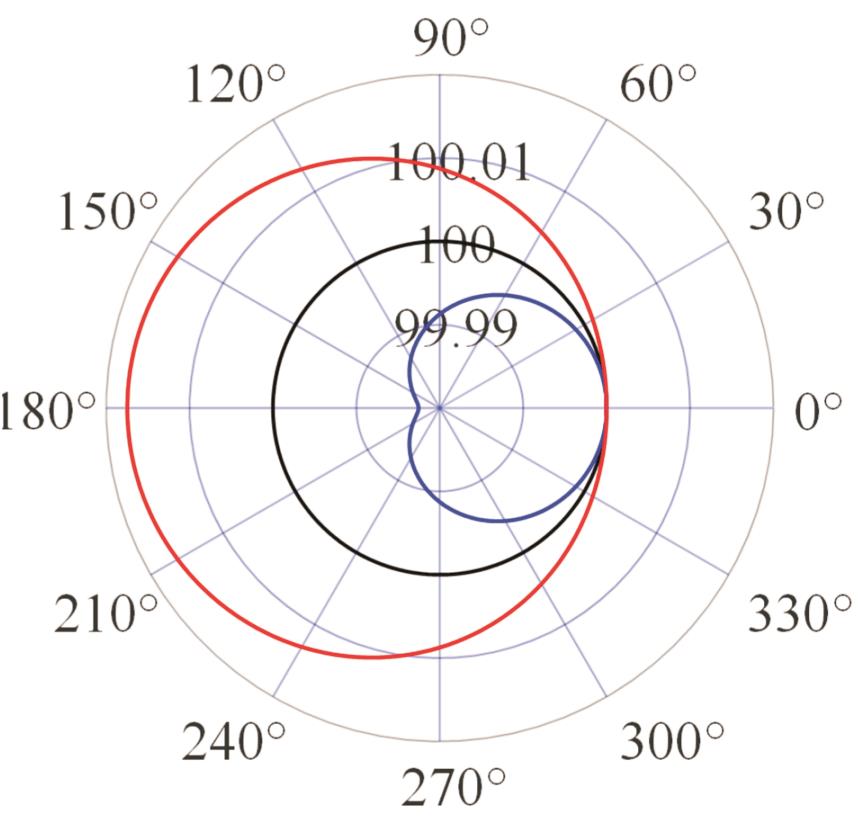 | ||
| 误差 | ||||
模式一 仅C轴 旋转 | 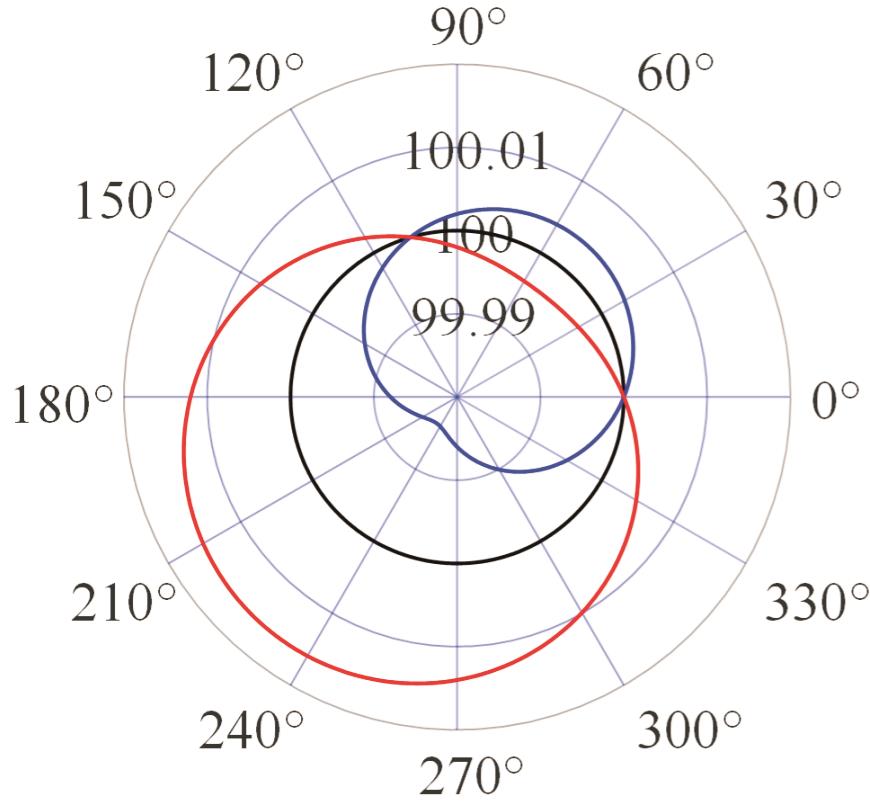 | 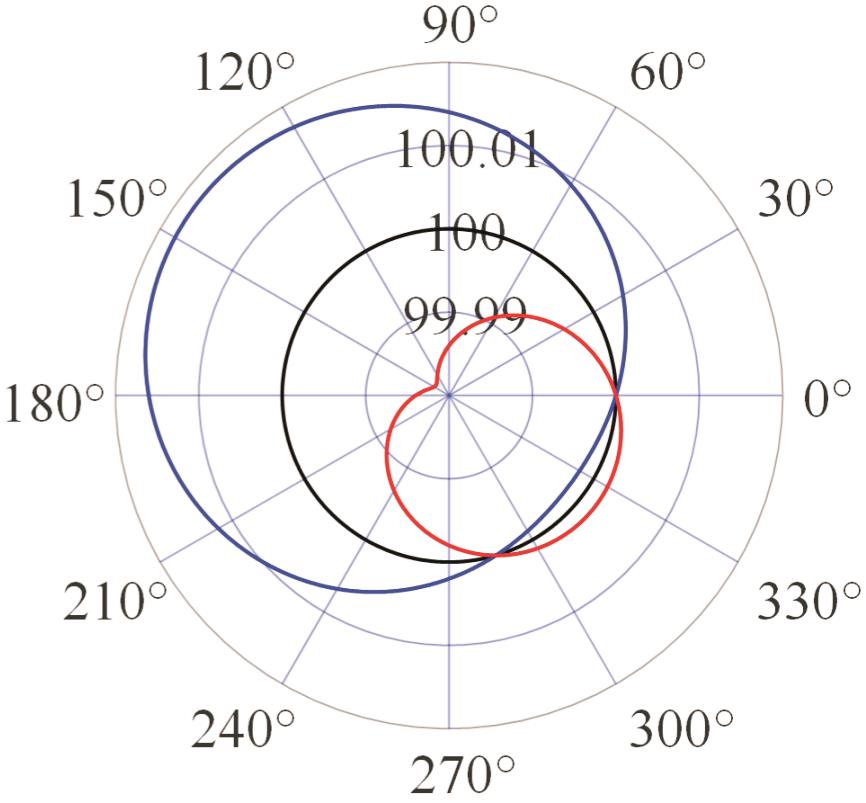 | 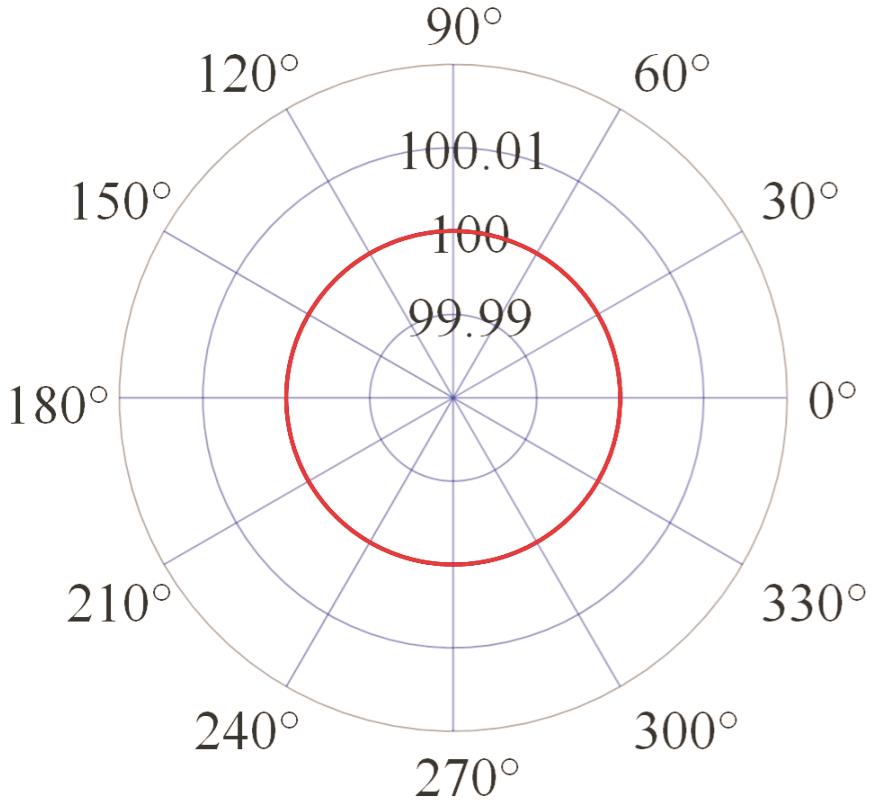 | 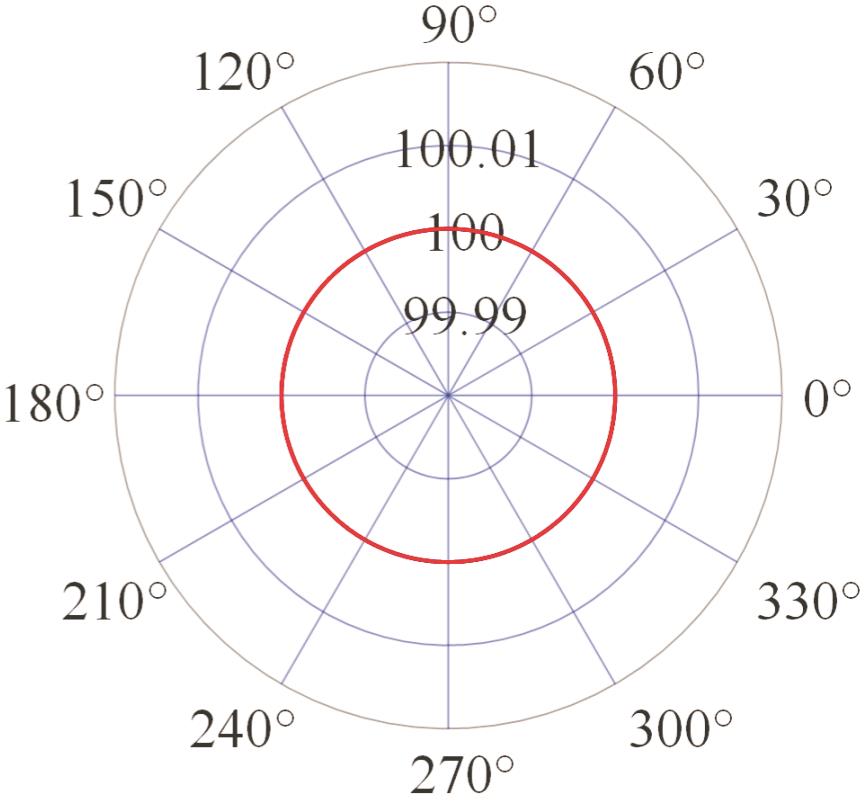 |
| 模式三 | 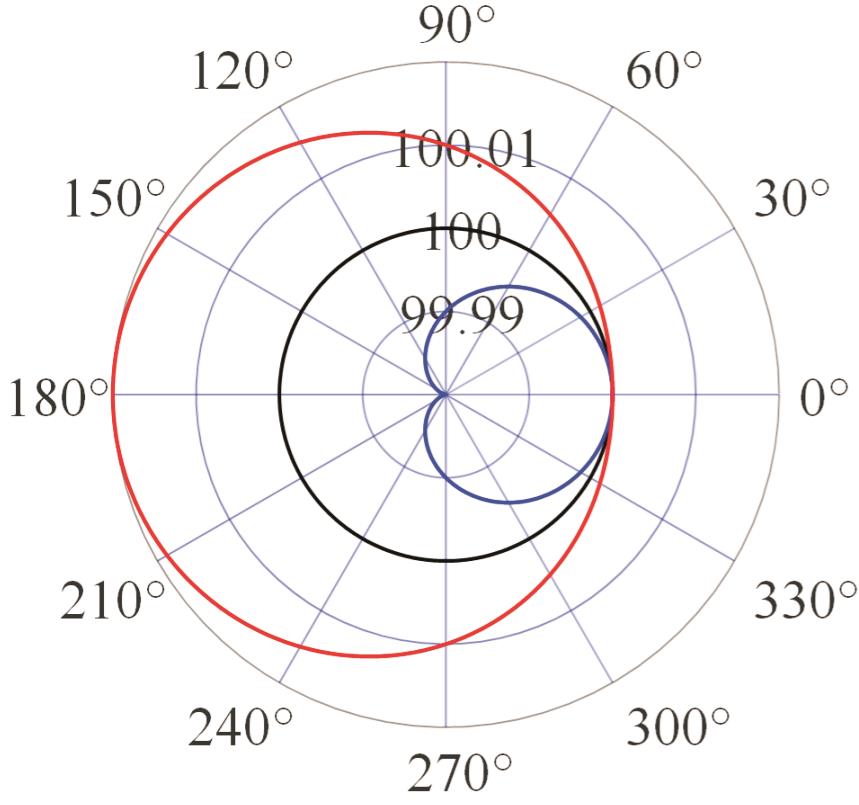 | 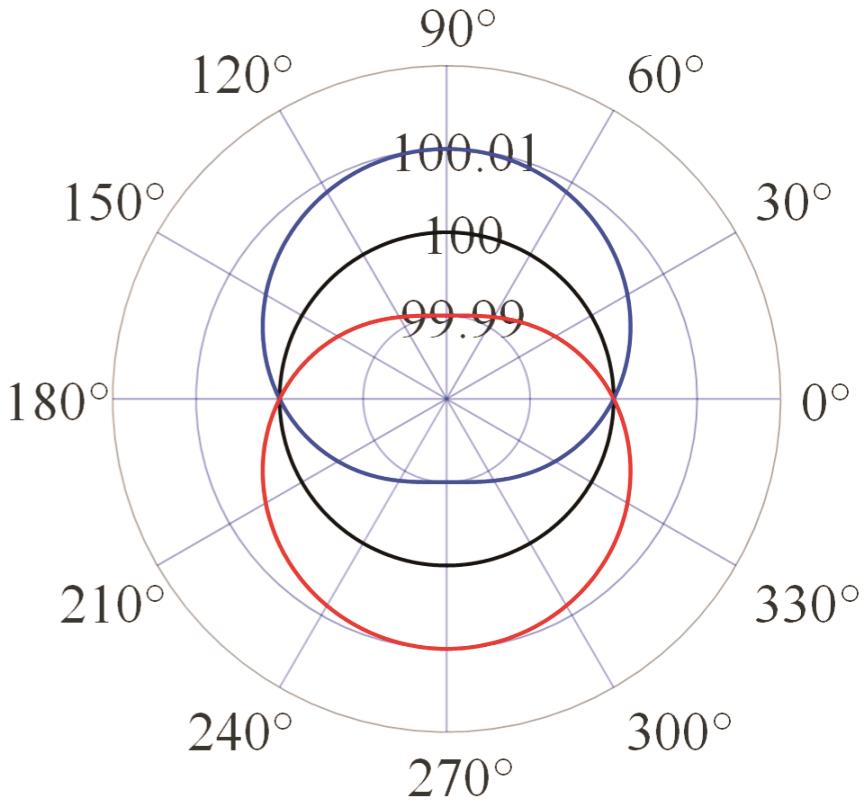 | 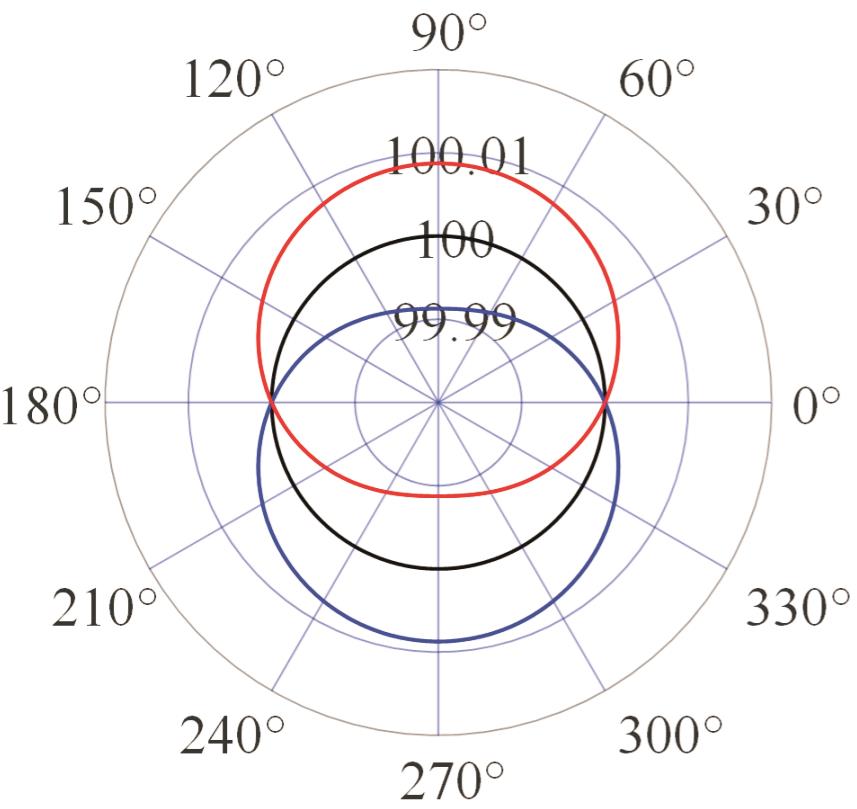 | 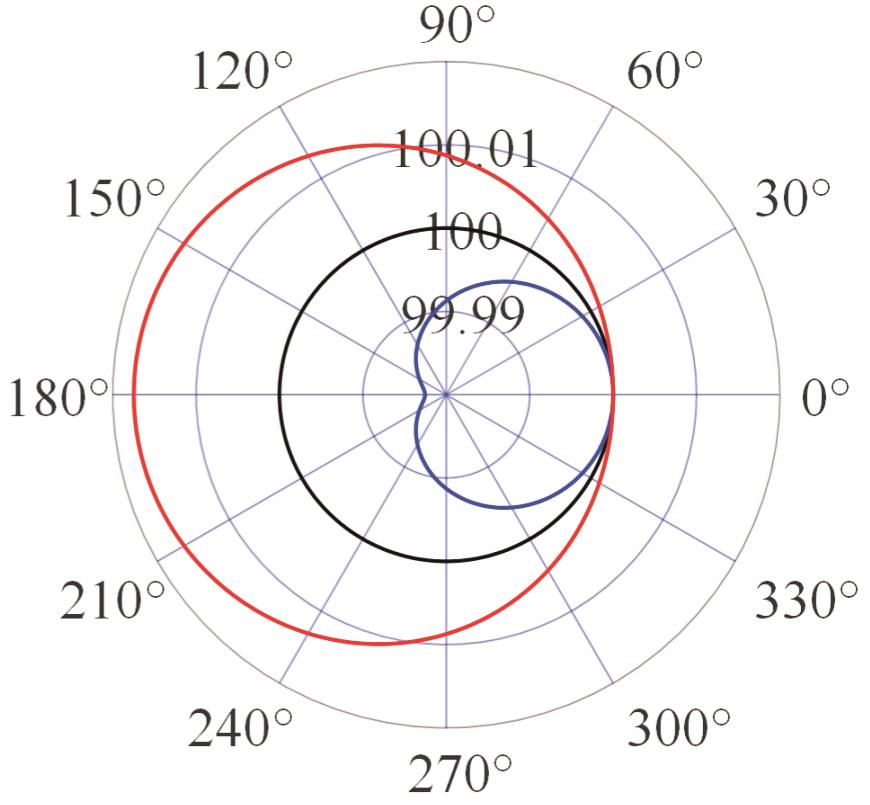 |
表2 PIGEs对各安装模式下杆长的影响
Tab.2 The influence of PIGEs on each installation mode
| 误差 | ||||
|---|---|---|---|---|
模式一 仅A轴 旋转 |  |  |  |  |
| 模式二 |  |  |  |  |
模式一 仅C轴 旋转 |  |  | ||
| 模式三 |  |  | ||
| 误差 | ||||
模式一 仅C轴 旋转 |  |  |  |  |
| 模式三 |  |  |  |  |
| 误差项 | 补偿前 | 补偿后 | 误差降低率/% |
|---|---|---|---|
| δYA /μm | 28.69 | -1.54 | 94.63 |
| δZA /μm | -103.90 | 0.46 | 99.56 |
| SYA /(″) | -6.68 | -2.16 | 67.66 |
| SZA /(″) | -13.60 | -4.06 | 70.15 |
| δXC /μm | 5.14 | 0.80 | 84.44 |
| δYC /μm | -6.73 | 1.22 | 81.87 |
| SXC /(″) | -16.03 | -3.64 | 77.29 |
| SYC /(″) | -26.34 | 3.05 | 88.42 |
表3 PIGEs补偿前后的数值
Tab.3 Values of PIGEs before and after compensation
| 误差项 | 补偿前 | 补偿后 | 误差降低率/% |
|---|---|---|---|
| δYA /μm | 28.69 | -1.54 | 94.63 |
| δZA /μm | -103.90 | 0.46 | 99.56 |
| SYA /(″) | -6.68 | -2.16 | 67.66 |
| SZA /(″) | -13.60 | -4.06 | 70.15 |
| δXC /μm | 5.14 | 0.80 | 84.44 |
| δYC /μm | -6.73 | 1.22 | 81.87 |
| SXC /(″) | -16.03 | -3.64 | 77.29 |
| SYC /(″) | -26.34 | 3.05 | 88.42 |
| 辨识方法 | 安装次数 | 指标 | δYA | δZA | SYA | SZA | δXC | δYC | SXC | SYC |
|---|---|---|---|---|---|---|---|---|---|---|
| 文献[ | 3 | 补偿前 | -27.13 μm | 1.90 μm | -12.47″ | -1.26″ | -23.36 μm | 214.20 μm | 103.99″ | 343.15″ |
| 补偿后 | -8.01 μm | 0.68 μm | -4.91″ | -0.40″ | -8.09 μm | 68.12 μm | 39.12″ | 115.68″ | ||
| 降低率 | 70.48% | 64.21% | 60.62% | 68.25% | 65.37% | 68.20% | 62.38% | 66.29% | ||
| 平均降低率 | 65.73% | |||||||||
| 文献[ | 4 | 补偿前 | 25.40 μm | -9.10 μm | 6.33″ | -0.93″ | 22.30 μm | 3.30 μm | 4.17″ | -0.95″ |
| 补偿后 | -1.00 μm | -0.20 μm | -0.83″ | -0.08″ | 4.00 μm | -2.00 μm | 0″ | 3.82″ | ||
| 降低率 | 96.06% | 97.80% | 86.89% | 91.40% | 82.06% | 39.39% | 100.00% | 0 | ||
| 平均降低率 | 74.20% | |||||||||
| 本文方法 | 3 | 补偿前 | 28.69 μm | -103.90 μm | -6.68″ | -13.60″ | 5.14 μm | -6.73 μm | -16.03″ | -26.34″ |
| 补偿后 | -1.54 μm | 0.46 μm | -2.16″ | -4.06″ | 0.80 μm | 1.22 μm | -3.64″ | 3.05″ | ||
| 降低率 | 94.63% | 99.56% | 67.66% | 70.15% | 84.44% | 81.87% | 77.29% | 88.42% | ||
| 平均降低率 | 83.00% | |||||||||
表4 PIGEs辨识方法的对比
Tab.4 Comparision among PIGEs identification methods
| 辨识方法 | 安装次数 | 指标 | δYA | δZA | SYA | SZA | δXC | δYC | SXC | SYC |
|---|---|---|---|---|---|---|---|---|---|---|
| 文献[ | 3 | 补偿前 | -27.13 μm | 1.90 μm | -12.47″ | -1.26″ | -23.36 μm | 214.20 μm | 103.99″ | 343.15″ |
| 补偿后 | -8.01 μm | 0.68 μm | -4.91″ | -0.40″ | -8.09 μm | 68.12 μm | 39.12″ | 115.68″ | ||
| 降低率 | 70.48% | 64.21% | 60.62% | 68.25% | 65.37% | 68.20% | 62.38% | 66.29% | ||
| 平均降低率 | 65.73% | |||||||||
| 文献[ | 4 | 补偿前 | 25.40 μm | -9.10 μm | 6.33″ | -0.93″ | 22.30 μm | 3.30 μm | 4.17″ | -0.95″ |
| 补偿后 | -1.00 μm | -0.20 μm | -0.83″ | -0.08″ | 4.00 μm | -2.00 μm | 0″ | 3.82″ | ||
| 降低率 | 96.06% | 97.80% | 86.89% | 91.40% | 82.06% | 39.39% | 100.00% | 0 | ||
| 平均降低率 | 74.20% | |||||||||
| 本文方法 | 3 | 补偿前 | 28.69 μm | -103.90 μm | -6.68″ | -13.60″ | 5.14 μm | -6.73 μm | -16.03″ | -26.34″ |
| 补偿后 | -1.54 μm | 0.46 μm | -2.16″ | -4.06″ | 0.80 μm | 1.22 μm | -3.64″ | 3.05″ | ||
| 降低率 | 94.63% | 99.56% | 67.66% | 70.15% | 84.44% | 81.87% | 77.29% | 88.42% | ||
| 平均降低率 | 83.00% | |||||||||
| [1] | CHEN Q, LI W, JIANG C, et al. Separation and Compensation of Geometric Errors of Rotary Axis in 5-Axis Ultra-precision Machine Tool by Empirical Mode Decomposition Method[J]. Journal of Manufacturing Processes, 2021, 68: 1509-1523. |
| [2] | LEE K I, YANG S H. Compensation of Position-independent and Position-dependent Geometric Errors in the Rotary Axes of Five-axis Machine Tools with a Tilting Rotary Table[J]. The International Journal of Advanced Manufacturing Technology, 2016, 85: 1677-1685. |
| [3] | JIANG X, CRIPPS R J. A Method of Testing Position Independent Geometric Errors in Rotary Axes of a Five-axis Machine Tool Using a Double Ball Bar[J]. International Journal of Machine Tools and Manufacture, 2015, 89: 151-158. |
| [4] | 郭世杰,张东升.五轴机床旋转轴几何误差分析与补偿[J]. 工程科学与技术,2020,52(2):130-139. |
| GUO Shijie, ZHANG Dongsheng. Geometric Error Analysis and Compensation of Rotary Axes of Five-axis Machine Tools[J]. Advanced Engineering Sciences,2020,52(2): 130-139. | |
| [5] | OSEI S, WANG W, DING Q. A New Method to Identify the Position-independent Geometric Errors in the Rotary Axes of Five-axis Machine Tools[J]. Journal of Manufacturing Processes, 2023, 87: 46-53. |
| [6] | WANG J, GUO J. The Identification Method of the Relative Position Relationship between the Rotary and Linear Axis of Multi-axis Numerical Control Machine Tool by Laser Tracker[J]. Measurement, 2019, 132: 369-376. |
| [7] | DENG M, LI H, XIANG S, et al. Geometric Errors Identification Considering Rigid-body Motion Constraint for Rotary Axis of Multi-axis Machine Tool Using a Tracking Interferometer[J]. International Journal of Machine Tools and Manufacture, 2020, 158: 103625. |
| [8] | JIANG Z, BAO S, ZHOU X, et al. Identification of Location Errors by a Touch-trigger Probe on Five-axis Machine Tools with a Tilting Head[J]. The International Journal of Advanced Manufacturing Technology, 2015, 81: 149-158. |
| [9] | HOLUB M, JANKOVYCH R, ANDRS O, et al. Capability Assessment of CNC Machining Centres as Measuring Devices[J]. Measurement, 2018, 118: 52-60. |
| [10] | HONG C, IBARAKI S, OYAMA C. Graphical Presentation of Error Motions of Rotary Axes on a Five-axis Machine Tool by Static R-test with Separating the Influence of Squareness Errors of Linear Axes[J]. International Journal of Machine Tools and Manufacture, 2012, 59: 24-33. |
| [11] | LI J, XIE F, LIU X J, et al. A Geometric Error Identification Method for the Swiveling Axes of Five-axis Machine Tools by Static R-test[J]. The International Journal of Advanced Manufacturing Techno- logy, 2017, 89: 3393-3405. |
| [12] | TSUTSUMI M, SAITO A. Identification and Compensation of Systematic Deviations Particular to 5-Axis Machining Centers[J]. International Journal of Machine Tools and Manufacture, 2003, 43(8): 771-780. |
| [13] | LEE K I, YANG S H. Measurement and Verification of Position-independent Geometric Errors of a Five-axis Machine Tool Using a Double Ball-bar[J]. International Journal of Machine Tools and Manufacture, 2013, 70: 45-52. |
| [14] | YANG J, DING H. A New Position Independent Geometric Errors Identification Model of Five-axis Serial Machine Tools Based on Differential Motion Matrices[J]. International Journal of Machine Tools and Manufacture, 2016, 104: 68-77. |
| [15] | LI Q, WANG W, ZHANG J, et al. All Position-dependent Geometric Error Identification for Rotary Axes of Five-axis Machine Tool Using Double Ball Bar[J]. The International Journal of Advanced Manufacturing Technology, 2020, 110: 1351-1366. |
| [16] | GUO S, JIANG G, ZHANG D, et al. Position-independent Geometric Error Identification and Global Sensitivity Analysis for the Rotary Axes of Five-axis Machine Tools[J]. Measurement Science and Technology, 2017, 28(4): 045006. |
| [17] | 项四通. 五轴数控机床空间误差测量、建模与补偿技术研究[D]. 上海:上海交通大学, 2016. |
| XIANG Sitong. Volumetric Error Measuring, Modeling and Compensation Technique for Five-axis Machine Tools[D]. Shanghai: Shanghai Jiao Tong University, 2016. | |
| [18] | 张文斌, 刘焕牢, 王宇林, 等. 双转台五轴数控机床旋转轴位置无关几何误差辨识[J]. 中国机械工程, 2024, 35 (6): 1023-1033. |
| ZHANG Wenbin, LIU Huanlao, WANG Yulin, et al. Identification of Rotary Axes PIGEs of Five-axis CNC Machines with Double Rotary Tables[J]. China Mechanical Engineering, 2024, 35 (6): 1023-1033. | |
| [19] | IX-ISO. Test Code for Machine Tools—Part 7: Geometric Accuracy of Axes of Rotation [S]. Geneva:ISO, 2015. |
| [20] | 夏长久, 王时龙, 徐凯, 等. 基于球杆仪单轴运动测量的旋转轴几何误差辨识[J]. 仪器仪表学报, 2020, 41(7): 19-28. |
| XIA Changjiu, WANG Shilong, XU Kai, et al. Geometric Error Identification of Rotary Axes Based on Uniaxial Motion Measurement of Double Ball Bar[J]. Chinese Journal of Scientific Instrument, 2020, 41(7): 19-28. | |
| [21] | IX-ISO. Test Code for Machine Tools–Part 1: Geometric Accuracy of Machines Operating under No-load or Quasi-static Conditions [S]. Geneva:ISO, 2012. |
| [1] | 李国龙1, 肖扬1, 李喆裕1, 徐凯2, 张薇1. 数控机床旋转轴多自由度静/热误差同步测量与建模[J]. 中国机械工程, 2024, 35(08): 1426-1434. |
| [2] | 张文斌, 刘焕牢, 王宇林, 周恒宇. 双转台五轴数控机床旋转轴位置无关几何误差辨识[J]. 中国机械工程, 2024, 35(06): 1023-1033. |
| [3] | 梁小冰, 卢耀安, 王成勇, . 双转台五轴机床旋转轴位置无关几何误差的辨识[J]. 中国机械工程, 2023, 34(21): 2585-2591. |
| [4] | 郑华林1;项锡平1;胡腾1;米良2;刘雁3. 五轴加工中心旋转轴几何误差元素区别建模辨识技术[J]. 中国机械工程, 2021, 32(05): 547-555. |
| [5] | 阮大文, 茅健, 刘钢, 马丽. [误差建模及精度保证方法]双五轴数控铣削机床旋转轴误差辨识方法[J]. 中国机械工程, 2020, 31(13): 1548-1554. |
| [6] | 陈光胜, 郑庆振. 一种多轴数控机床末端静刚度快速辨识方法[J]. 中国机械工程, 2017, 28(03): 322-326. |
| [7] | 林述温, 吴城汀, 林清锋. 数控机床旋转轴误差的快速测量与辨识新方法[J]. 中国机械工程, 2014, 25(9): 1169-1174. |
| [8] | 江磊, 李庄, 李相标, 周良明, 段昌德, 丁国富. 无限旋转C轴工作台结构的五轴机床后置转角求解[J]. 中国机械工程, 2014, 25(16): 2178-2183. |
| [9] | 王秀山;杨建国;余永昌;邹彩虹;. 双转台五轴数控机床热误差建模、检测及补偿实验研究[J]. J4, 2009, 20(04): 0-388. |
| [10] | 张大卫;商鹏;田延岭;贺琼义;. 五轴数控机床转动轴误差元素的球杆仪检测方法[J]. J4, 2008, 19(22): 0-2649. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||