



ISSN 1004-132X
CN 42-1294/TH
CN 42-1294/TH




中国机械工程 ›› 2026, Vol. 37 ›› Issue (1): 174-183.DOI: 10.3969/j.issn.1004-132X.2026.01.018
• 智能制造 • 上一篇
王浩1,2( ), 罗浩东3, 施亚中4, 王立文5(
), 罗浩东3, 施亚中4, 王立文5( ), 张威5, 王忠6
), 张威5, 王忠6
收稿日期:2024-11-20
出版日期:2026-01-25
发布日期:2026-02-05
通讯作者:
王立文
作者简介:王浩,男,1985年生,硕士研究生。研究方向为航空器智慧维修、增材制件结构拓扑优化。发表论文5篇。E-mail: wanghao@cauc.edu.cn基金资助:
WANG Hao1,2( ), LUO Haodong3, SHI Yazhong4, WANG Liwen5(
), LUO Haodong3, SHI Yazhong4, WANG Liwen5( ), ZHANG Wei5, WANG Zhong6
), ZHANG Wei5, WANG Zhong6
Received:2024-11-20
Online:2026-01-25
Published:2026-02-05
Contact:
WANG Liwen
摘要:
针对结构拓扑优化中的“灰度单元”问题和“计算成本”挑战,提出一种基于端到端深度学习模型TOPO-U-Net的结构拓扑优化方法,该模型包括高低阶特征提取模块、深度可分卷积、组归一化,并设计了一种基于中间密度单元偏移函数的评价方法。实验结果表明,所提模型的中间密度偏移率达到85.42%,平均优化计算时间仅为固体各向同性材料惩罚模型方法的1%,显著减少了“灰度单元”数量,提高了设计的可制造性和结构拓扑优化的效率。
中图分类号:
王浩, 罗浩东, 施亚中, 王立文, 张威, 王忠. 基于端到端深度学习模型TOPO-U型网的结构拓扑优化方法[J]. 中国机械工程, 2026, 37(1): 174-183.
WANG Hao, LUO Haodong, SHI Yazhong, WANG Liwen, ZHANG Wei, WANG Zhong. A Topology Optimization Method Based on End-to-end Deep Learning Framework TOPO-U-Net[J]. China Mechanical Engineering, 2026, 37(1): 174-183.
| 训练参数 | 设置 | 说明 |
|---|---|---|
| 优化器 | Adam | 梯度下降算法 |
| 学习率 | 0.001 | 初始学习率 |
| 批大小 | 8 | 每次训练的样本数 |
| 轮次 | 200 | 总训练轮次 |
| CUDNN | enable | GPU加速库 |
表1 模型训练过程的超参数
Tab.1 Hyperparameters of the model training process
| 训练参数 | 设置 | 说明 |
|---|---|---|
| 优化器 | Adam | 梯度下降算法 |
| 学习率 | 0.001 | 初始学习率 |
| 批大小 | 8 | 每次训练的样本数 |
| 轮次 | 200 | 总训练轮次 |
| CUDNN | enable | GPU加速库 |
| IID | RIDD/% | RVFE/% | EMA | |
|---|---|---|---|---|
| 未引入HLFE | 0.6735 | 83.68 | 2.97 | 0.0663 |
| 引入HLFE | 0.7084 | 85.42 | 2.96 | 0.0651 |
表2 HLFE模块消融实验效果对比
Tab.2 Comparison of HLFE module ablation experiment
| IID | RIDD/% | RVFE/% | EMA | |
|---|---|---|---|---|
| 未引入HLFE | 0.6735 | 83.68 | 2.97 | 0.0663 |
| 引入HLFE | 0.7084 | 85.42 | 2.96 | 0.0651 |
| 不同模型 | IID | RIDD/% | RVFE/% | EMA |
|---|---|---|---|---|
| U-Net | 0.6798 | 83.99 | 3.76 | 0.0669 |
| Resnet | 0.6467 | 82.34 | 2.94 | 0.0690 |
| TOPO-U-Net | 0.7084 | 85.42 | 2.96 | 0.0651 |
表3 三种神经网络模型的对比
Tab.3 Comparison of three deep learning models
| 不同模型 | IID | RIDD/% | RVFE/% | EMA |
|---|---|---|---|---|
| U-Net | 0.6798 | 83.99 | 3.76 | 0.0669 |
| Resnet | 0.6467 | 82.34 | 2.94 | 0.0690 |
| TOPO-U-Net | 0.7084 | 85.42 | 2.96 | 0.0651 |
| 密度范围 | 方法 | 平均分布 | 密度范围 | 方法 | 平均分布 |
|---|---|---|---|---|---|
| [0, 0.1] | SIMP | 1011.1290 | (0.5, 0.7] | SIMP | 134.3720 |
| MSE | 994.8630 | MSE | 127.5620 | ||
| BCE | 976.6470 | BCE | 129.0490 | ||
| DICE | 1254.0620 | DICE | 2.4320 | ||
| (0.1, 0.3] | SIMP | 155.9580 | (0.7, 0.9] | SIMP | 178.0110 |
| MSE | 175.7750 | MSE | 204.0700 | ||
| BCE | 170.0760 | BCE | 200.2030 | ||
| DICE | 3.8410 | DICE | 3.8170 | ||
| (0.3, 0.5] | SIMP | 122.0810 | (0.9, 1.0] | SIMP | 1598.4490 |
| MSE | 123.3500 | MSE | 1574.3800 | ||
| BCE | 125.0660 | BCE | 1598.9590 | ||
| DICE | 2.4820 | DICE | 1933.3660 |
表4 四种方法在六种密度范围内的平均分布
Tab.4 Average distribution within 6 different density ranges for 4 methods
| 密度范围 | 方法 | 平均分布 | 密度范围 | 方法 | 平均分布 |
|---|---|---|---|---|---|
| [0, 0.1] | SIMP | 1011.1290 | (0.5, 0.7] | SIMP | 134.3720 |
| MSE | 994.8630 | MSE | 127.5620 | ||
| BCE | 976.6470 | BCE | 129.0490 | ||
| DICE | 1254.0620 | DICE | 2.4320 | ||
| (0.1, 0.3] | SIMP | 155.9580 | (0.7, 0.9] | SIMP | 178.0110 |
| MSE | 175.7750 | MSE | 204.0700 | ||
| BCE | 170.0760 | BCE | 200.2030 | ||
| DICE | 3.8410 | DICE | 3.8170 | ||
| (0.3, 0.5] | SIMP | 122.0810 | (0.9, 1.0] | SIMP | 1598.4490 |
| MSE | 123.3500 | MSE | 1574.3800 | ||
| BCE | 125.0660 | BCE | 1598.9590 | ||
| DICE | 2.4820 | DICE | 1933.3660 |
| 密度范围 | 方法 | 平均分布 | 密度范围 | 方法 | 平均分布 |
|---|---|---|---|---|---|
| [0, 0.1] | SIMP | 1011.1290 | (0.5, 0.7] | SIMP | 134.3720 |
| MSE | 81.1290 | MSE | 67.7520 | ||
| BCE | 68.5380 | BCE | 82.0020 | ||
| DICE | 398.9640 | DICE | 110.5270 | ||
| (0.1, 0.3] | SIMP | 155.9580 | (0.7, 0.9] | SIMP | 178.0110 |
| MSE | 87.7060 | MSE | 94.1190 | ||
| BCE | 66.3910 | BCE | 108.0310 | ||
| DICE | 143.3360 | DICE | 171.4260 | ||
| (0.3, 0.5] | SIMP | 122.0810 | (0.9, 1] | SIMP | 1598.4490 |
| MSE | 67.3130 | MSE | 40.9640 | ||
| BCE | 50.3680 | BCE | 45.2150 | ||
| DICE | 77.6050 | DICE | 116.5720 |
表5 4种方法的中间密度偏移的平均分布
Tab.5 Average distribution of IDDR for 4 methods
| 密度范围 | 方法 | 平均分布 | 密度范围 | 方法 | 平均分布 |
|---|---|---|---|---|---|
| [0, 0.1] | SIMP | 1011.1290 | (0.5, 0.7] | SIMP | 134.3720 |
| MSE | 81.1290 | MSE | 67.7520 | ||
| BCE | 68.5380 | BCE | 82.0020 | ||
| DICE | 398.9640 | DICE | 110.5270 | ||
| (0.1, 0.3] | SIMP | 155.9580 | (0.7, 0.9] | SIMP | 178.0110 |
| MSE | 87.7060 | MSE | 94.1190 | ||
| BCE | 66.3910 | BCE | 108.0310 | ||
| DICE | 143.3360 | DICE | 171.4260 | ||
| (0.3, 0.5] | SIMP | 122.0810 | (0.9, 1] | SIMP | 1598.4490 |
| MSE | 67.3130 | MSE | 40.9640 | ||
| BCE | 50.3680 | BCE | 45.2150 | ||
| DICE | 77.6050 | DICE | 116.5720 |
| 工况 |  |  |  |  | 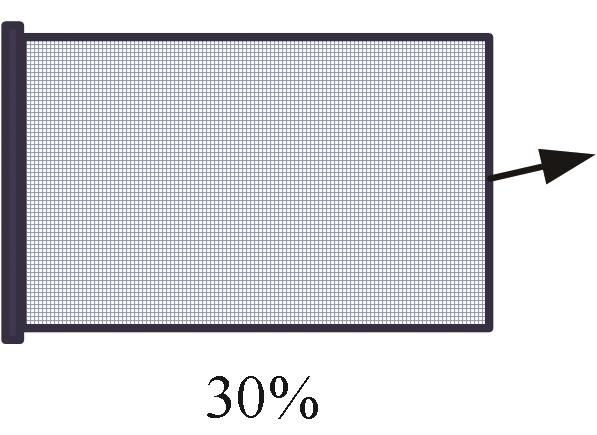 |
|---|---|---|---|---|---|
| SIMP | 2.04 | 2.03 | 1.02 | 0.82 | 0.18 |
| 本文方法 | 0.01 | 0.01 | 0.0099 | 0.0099 | 0.01 |
| 工况 | 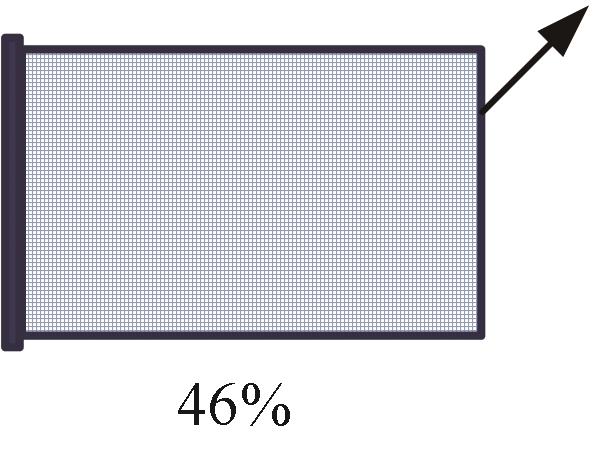 | 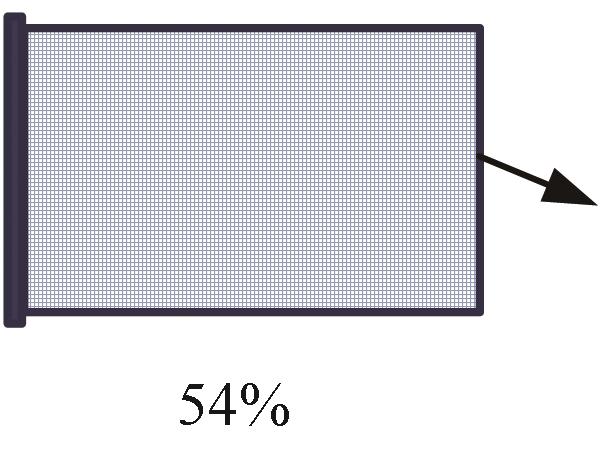 | 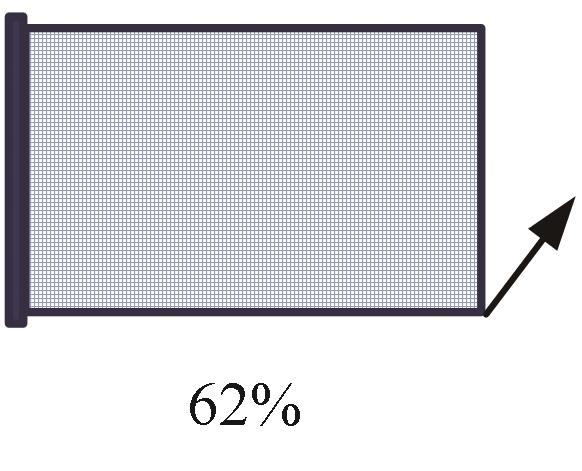 |  |  |
| SIMP | 1.46 | 0.6 | 1.15 | 0.94 | 1.21 |
| 本文方法 | 0.009 | 0.0099 | 0.01 | 0.01 | 0.01 |
表6 拓扑优化计算时间 (s)
Tab.6 Computational time of topology optimizations
| 工况 |  |  |  |  |  |
|---|---|---|---|---|---|
| SIMP | 2.04 | 2.03 | 1.02 | 0.82 | 0.18 |
| 本文方法 | 0.01 | 0.01 | 0.0099 | 0.0099 | 0.01 |
| 工况 |  |  |  |  |  |
| SIMP | 1.46 | 0.6 | 1.15 | 0.94 | 1.21 |
| 本文方法 | 0.009 | 0.0099 | 0.01 | 0.01 | 0.01 |
| 柔度误差率 | 样本分布数 | 柔度误差率 | 样本分布数 |
|---|---|---|---|
| ( | 0 | [0,0.1) | 47 |
| [ | 19 | [0.1,0.2) | 4 |
| [ | 34 | [0.2,0.6) | 2 |
| [ | 122 | [0.6,1) | 1 |
| [ | 766 | ≥1 | 5 |
表7 测试集样本在不同柔度误差率的分布
Tab.7 Distribution of test-dataset samples in different compliance error rates
| 柔度误差率 | 样本分布数 | 柔度误差率 | 样本分布数 |
|---|---|---|---|
| ( | 0 | [0,0.1) | 47 |
| [ | 19 | [0.1,0.2) | 4 |
| [ | 34 | [0.2,0.6) | 2 |
| [ | 122 | [0.6,1) | 1 |
| [ | 766 | ≥1 | 5 |
| 孤立区域数 | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 大于3 | |
| SIMP | 998 | 2 | 0 | 0 |
| TOPO-U-Net模型 | 981 | 17 | 2 | 0 |
表8 两种方法结果中的孤立区域数目对比
Tab.8 Comparison of the number of isolated regions
| 孤立区域数 | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 大于3 | |
| SIMP | 998 | 2 | 0 | 0 |
| TOPO-U-Net模型 | 981 | 17 | 2 | 0 |
| [1] | BENDSØE M P, KIKUCHI N. Generating Optimal Topologies in Structural Design Using a Homogenization Method[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 71(2): 197-224. |
| [2] | ZHOU M, ROZVANY G I N. The COC Algorithm, Part II: Topological, Geometrical and Generalized Shape Optimization[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 89(1/3): 309-336. |
| [3] | XIE Y M, STEVEN G P. A Simple Evolutionary Procedure for Structural Optimization[J]. Computers & Structures, 1993, 49(5): 885-896. |
| [4] | WANG M Y, WANG Xiaoming, GUO Dongming. A Level Set Method for Structural Topology Optimization[J]. Computer Methods in Applied Mechanics and Engineering, 2003, 192(1/2): 227-246. |
| [5] | GUO Xu, ZHANG Weisheng, ZHONG Wenliang. Doing Topology Optimization Explicitly and Geometrically—a New Moving Morphable Components Based Framework[J]. Journal of Applied Mechanics, 2014, 81(8): 081009. |
| [6] | SOSNOVIK I, OSELEDETS I. Neural Networks for Topology Optimization[J]. Russian Journal of Numerical Analysis and Mathematical Modelling, 2019, 34(4): 215-223. |
| [7] | QIU Cheng, DU Shanyi, YANG Jinglei. A Deep Learning Approach for Efficient Topology Optimization Based on the Element Removal Strategy[J]. Materials & Design, 2021, 212: 110179. |
| [8] | SENHORA F V, CHI Heng, ZHANG Yuyu, et al. Machine Learning for Topology Optimization: Physics-based Learning through an Independent Training Strategy[J]. Computer Methods in Applied Mechanics and Engineering, 2022, 398: 115116. |
| [9] | YAN Jun, ZHANG Qi, XU Qi, et al. Deep Learning Driven Real Time Topology Optimisation Based on Initial Stress Learning[J]. Advanced Engineering Informatics, 2022, 51: 101472. |
| [10] | ABUEIDDA D W, KORIC S, SOBH N A. Topology Optimization of 2D Structures with Nonlinearities Using Deep Learning[J]. Computers & Structures, 2020, 237: 106283. |
| [11] | SEO J, KAPANIA R K. Topology Optimization with Advanced CNN Using Mapped Physics-based Data[J]. Structural and Multidisciplinary Optimization, 2023, 66(1): 21. |
| [12] | WANG Dalei, XIANG Cheng, PAN Yue, et al. A Deep Convolutional Neural Network for Topology Optimization with Perceptible Generalization Ability[J]. Engineering Optimization, 2022, 54(6): 973-988. |
| [13] | XIANG Cheng, WANG Dalei, PAN Yue, et al. Accelerated Topology Optimization Design of 3D Structures Based on Deep Learning[J]. Structural and Multidisciplinary Optimization, 2022, 65(3): 99. |
| [14] | 李振荣, 夏利娟, 冯朔. 基于UNet深度学习的VLCC横框架拓扑优化分析[J]. 中国舰船研究, 2024, 19(6): 108-116. |
| LI Zhenrong, XIA Lijuan, FENG Shuo. Topology Optimization Analysis of VLCC Transverse Web Based on UNet Deep Learning[J]. Chinese Journal of Ship Research, 2024, 19(6): 108-116. | |
| [15] | 项程, 陈艾荣. 基于深度学习的多材料结构拓扑优化方法[J]. 同济大学学报(自然科学版), 2022, 50(7): 975-982. |
| XIANG Cheng, CHEN Airong. Topology Optimization of Multimaterial Structures Based on Deep Learning[J]. Journal of Tongji University (Natural Science), 2022, 50(7): 975-982. | |
| [16] | RONNEBERGER O, FISCHER P, BROX T. U-Net: Convolutional Networks for Biomedical Image Segmentation[M]∥Medical Image Computing and Computer-assisted Intervention—MICCAI 2015. Cham: Springer International Publishing, 2015: 234-241. |
| [17] | WU Y, HE K. Group Normalization [C]∥Proceedings of the European Conference on Computer Vision(ECCV), Lecture Notes in Computer Science. Munich, 2018: 3-19. |
| [18] | LEI B J, KIROS J R, HINTON G E. Layer normalization[EB/OL]. ArXiv e-prints, 2016: arXiv:. |
| [19] | YAN Jun, GENG Dongling, XU Qi, et al. Real-time Topology Optimization Based on Convolutional Neural Network by Using Retrain Skill[J]. Engineering with Computers, 2023, 39(6): 4045-4059. |
| [20] | ANDREASSEN E, CLAUSEN A, SCHEVENELS M, et al. Efficient Topology Optimization in MATLAB Using 88 Lines of Code[J]. Structural and Multidisciplinary Optimization, 2011, 43(1): 1-16. |
| [1] | 何昆, 周和超, 张济民. 列车防爬吸能器负泊松比超材料填充结构设计[J]. 中国机械工程, 2025, 36(12): 3040-3046. |
| [2] | 闫祖龙, 庞启龙, 熊建龙. 基于深度学习的KDP晶体三维已加工表面形貌预测[J]. 中国机械工程, 2025, 36(10): 2329-2334. |
| [3] | 黄昊1, 王曾2, 李波2, 卢泽华1, 刘怀举1. 基于折衷规划法的航发齿轮传动壳体结构热柔度协同拓扑优化[J]. 中国机械工程, 2025, 36(07): 1471-1478. |
| [4] | 赵昀杰, 贺岩松, 张志飞, 徐中明. 基于生成模型的三维波束形成图像压缩方法[J]. 中国机械工程, 2025, 36(07): 1520-1529. |
| [5] | 苏珂1, 王颖1, 梁腾腾1, 魏义礼2, 张楠楠2. 基于知情构造理论的单材料柔性机构拓扑优化[J]. 中国机械工程, 2025, 36(04): 873-881. |
| [6] | 林家辉, 李壮壮, 李学霖, 李军. 一种路径吞噬拓扑优化新方法[J]. 中国机械工程, 2025, 36(03): 504-514. |
| [7] | 王书亭1, 谢晴天1, 杨奥迪1, 李小兵2, 熊体凡1, 谢贤达2. 等几何拓扑优化非齐次边界条件施加技术研究[J]. 中国机械工程, 2025, 36(03): 525-535. |
| [8] | 刘敏1, 2, 卢飞扬1, 占金青1, 2, 吴剑1, 朱本亮3. 考虑最小尺寸约束的内嵌可移动压电驱动柔顺机构拓扑优化设计[J]. 中国机械工程, 2025, 36(02): 255-264. |
| [9] | 曾浩, 曹华军, 董俭雄. 基于ISABO-IBiLSTM模型的刀具磨损预测方法[J]. 中国机械工程, 2024, 35(11): 1995-2006. |
| [10] | 李悦1, 2, 谢恒1, 周公博1, 2, 周坪1, 2, 李猛钢1, 2. 基于半监督贝叶斯Transformer的刀具磨损软测量及不确定性分析方法[J]. 中国机械工程, 2024, 35(11): 2015-2025. |
| [11] | 王浩1, 2, 王江北3, 罗浩东3, 王立文4. 基于改进四叉树和比例边界有限元法的自适应设计域拓扑优化方法[J]. 中国机械工程, 2024, 35(05): 904-915,927. |
| [12] | 杨峰, 罗世杰, 杨江鸿, 王英俊, . 基于GPU加速的等几何拓扑优化高效多重网格求解方法[J]. 中国机械工程, 2024, 35(04): 602-613. |
| [13] | 苏永雷, 张志飞. 车身多性能约束下的一体压铸三角梁轻量化设计[J]. 中国机械工程, 2024, 35(04): 691-699. |
| [14] | 李荣启, 闫涛, 何智成, 米栋, 姜潮, 郑静. 流-热-力耦合的高性能结构拓扑优化设计方法[J]. 中国机械工程, 2024, 35(03): 487-497. |
| [15] | 王超, 成艾国, 张承霖, 于万元, 何智成. 面向刮底安全的电池包防护结构轻量化设计[J]. 中国机械工程, 2023, 34(19): 2343-2352. |
| 阅读次数 | ||||||
|
全文 |
|
|||||
|
摘要 |
|
|||||