0 引言
在航空航天、国防工业、汽车制造等领域,经常用到大型机械臂完成对物体的自动转载、精密装配和精细操作等任务。例如美国国际空间站机械臂需要对往返天地之间的货运飞船进行捕获,对有效载荷在轨进行安装维修等,而这些操作都需要精确定位;汽车工业中的单臂工业机器人作为当今世界上技术最成熟的串联机械臂,被广泛应用于点焊、弧焊、喷漆、装货、卸货、包装等领域。但由于机械臂加工装配误差、传动机构间隙、摩擦磨损、环境影响等原因导致的回程误差、振动干扰使得机械臂实际的运动性能与期望的高精度运动性能相比还有较大的差距,因此,对提高串联机械臂运动精度的关键技术展开研究具有非常重要的意义。
一直以来,国内外诸多学者对提高串联机械臂精度的研究从未间断过,研究的主要内容有:模型的精确标定、机器视觉技术、多传感器融合的感知系统、智能控制系统及先进控制算法、轻量化设计等,并取得了很好的效果[1-2]。
串联机械臂的精度取决于许多因素的交互影响,以上研究虽然提高了串联机械臂运动精度性能,但没有在根本上解决传动间隙、摩擦磨损等原始误差以及实际运动过程中机械臂负载变化、加减速等原因造成的运动偏差及机械冲击振动,从而影响机械臂的动态性能与稳态精度。由于回程间隙的存在,那么单电机驱动时只要出现换向运动,电机侧就会与负载侧脱开,负载处于不可控状态,在换向过程中,负载自由衰减运动,会短时偏离期望的运动轨迹,对于高精度跟踪伺服系统来说,会引入回程误差。而当电机侧反向运动与负载重新接触瞬间,会产生严重的冲击振荡和噪声,加速齿轮的磨损,影响伺服系统的跟踪精度和定位精度。
为消除传动的非线性间隙,国内外科研人员对多电机驱动联动控制系统进行了探讨。KOREN[3]提出基于补偿原理的交叉耦合控制方法;TOMIZUKA等[4]将自适应前馈控制用于交叉耦合控制器中,以提高瞬态响应和抗干扰能力;SRINIVASAN等[5]采用时变交叉耦合控制器来满足系统对轨迹曲线跟踪的要求;陈庆伟等[6]建立了含齿隙双电机同步联动伺服系统的动力学模型,但没有考虑传动轴的柔性,不适用于传动链长而复杂的系统;朱国力等[7]设计的双电机联动消隙控制技术可应用于雷达天线的伺服驱动,但不适用于负载频繁变化的机械臂系统。
本文设计了双电机主从驱动消隙伺服系统,并根据动力学关系对该系统进行了Simulink建模,采用软件仿真验证了其可行性。硬件电路设计及其实际应用后误差测量结果证明了该系统能够提高机械臂精度性能,从根本上解决回程间隙问题,对精密机械系统有重要的应用价值。
1 双电机主从驱动消隙的原理
1.1 双电机驱动系统的传动形式
双电机驱动系统的机械连接和传动件主要有齿轮、蜗轮蜗杆、齿轮齿条和丝杠等[4-6]。本文所用的串联机械臂关节轴内部传动形式为两台电机通过齿轮驱动转台的传动结构,驱动电机在空间上为对称布置,如图1所示。
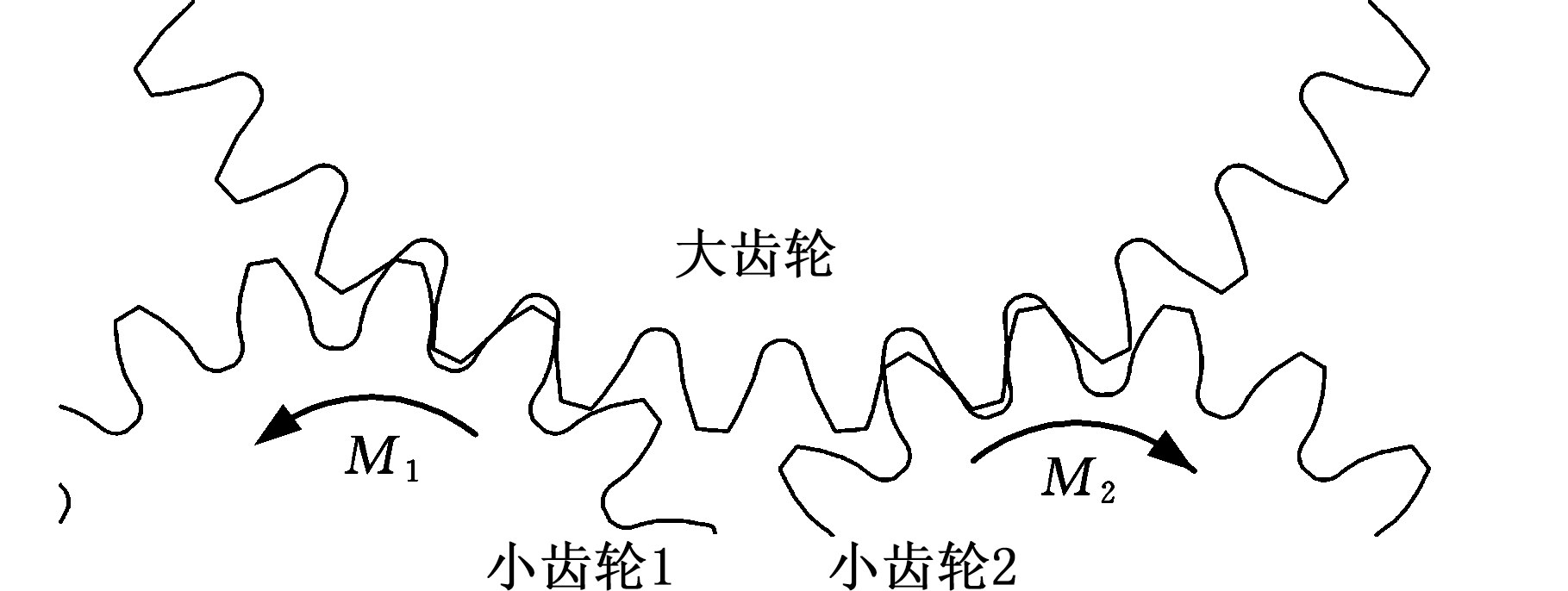
图1 消隙传动结构图
Fig.1 Structure diagram of anti-backlash transmission
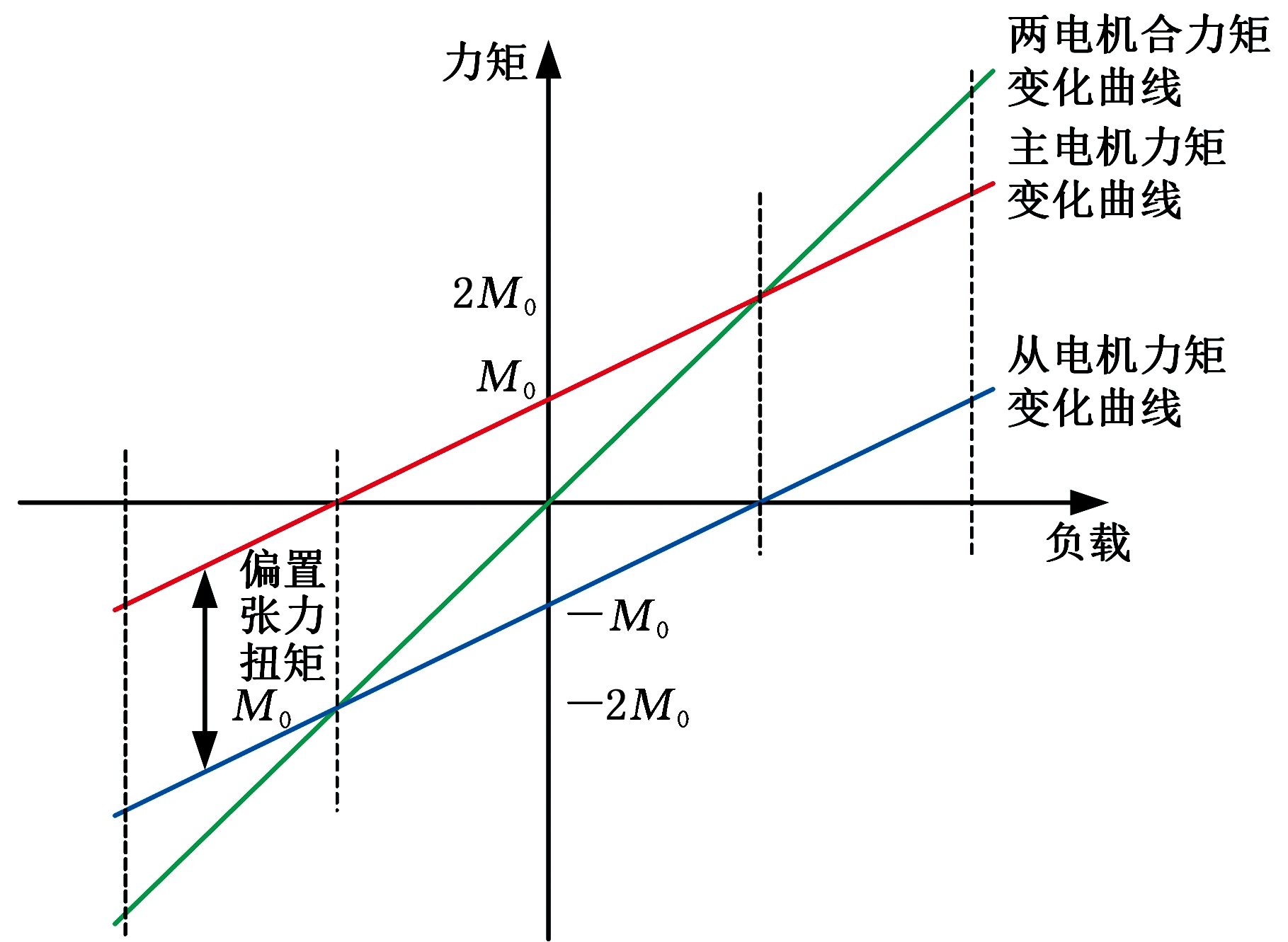
图2 双电机驱动消隙过程
Fig.2 Anti-backlash process diagram of
dual-motor driver
1.2 双电机驱动消隙过程
在关节轴启动过程中,如图2所示,两个电机提供大小相等、方向相反的力矩M0,形成一偏置力矩,使得两个小齿轮分别贴紧主齿轮的两个相反的啮合面,主齿轮不能在齿轮的间隙内摆动。随着一个小齿轮输出力矩的增大,另一个小齿轮力矩减小到0后,换向并逐渐增大输出力矩,这样带动主齿轮转动以达到平稳的工作状态。在换向过程中,两个电机的工作状况不同:一个电机维持平稳的转动状态,另一个电机提前改变力矩方向,使该电机驱动的小齿轮贴向主齿轮的另一个啮合面,再次形成偏置力矩,又回到启动时的偏置力矩状态,该力矩逐步增大,然后由提前反向的电机带动主齿轮转动,另一个电机才逐步反向,直到和前一电机共同分担负载转矩,从而使关节轴又达到平稳状态。
2 双电机消隙的建模与仿真
2.1 齿隙模型
常见的齿隙模型包括迟滞模型、弹性死区模型、冲击模型等,应根据实际应用场合的特点选取合适的模型。死区非线性模型是通过驱动与负载之间的传递力矩变化特性来描述齿隙的,同时考虑了机械系统刚度及内部阻尼的影响,是目前广泛采用的齿隙模型,如图3所示,它能够较真实地反映两实体相互碰撞的实际物理过程。其数学模型表述为
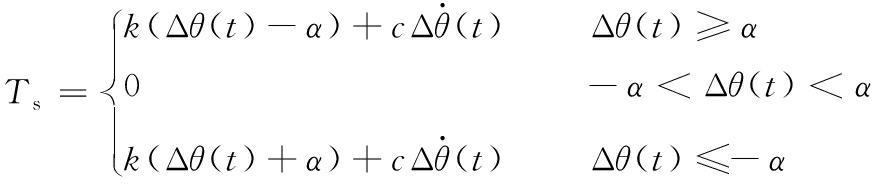
(1)
式中,Ts为阻力矩;Δθ(t)为以输入侧为基准的角差;k为刚度系数;c为内部阻尼系数;θin为输入角度;θout为输出角度;m为传动比;2α为齿隙角。
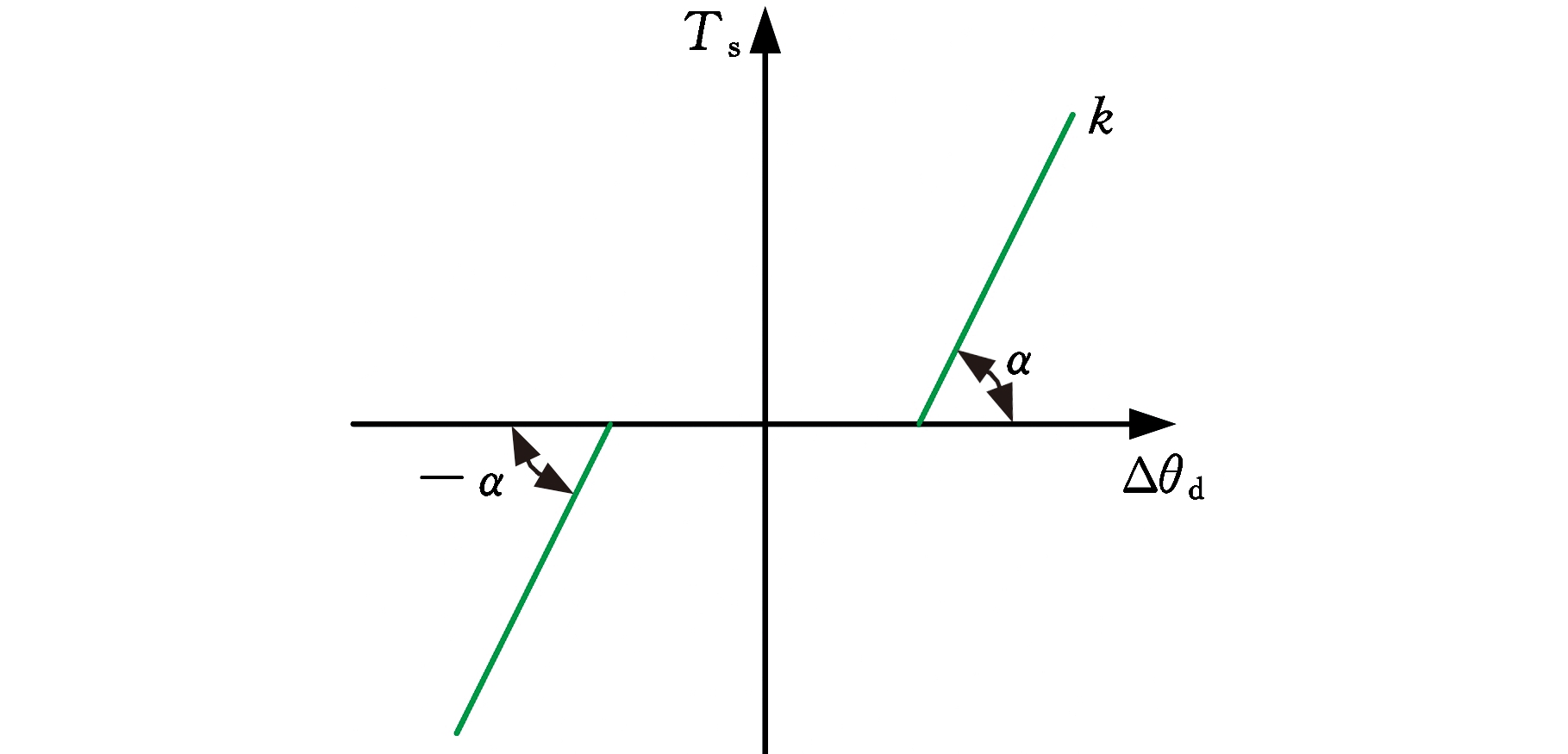
图3 回程齿隙弹性死区模型
Fig.3 Elastic dead-zone model of return backlash
2.2 双电机消隙模型
为了建立双电机驱动的动力学模型,需要分析系统结构。串联机械臂双电机消隙驱动系统可等效为由两个具有完全相同参数的电动机分别带动一个相同模数的小齿轮,按对称结构,通过小齿轮与大齿轮啮合,共同驱动一个带负载的大齿轮转动。俯仰关节与扭转关节的系统结构简图见图4、图5。其中,U1、U2为两个电机的电枢电压;ω1、ω2为两个伺服电机的角速度;i为减速器的传动比;ωc1、ωc2为两个小齿轮的角速度;Jc1、Jc2为两个小齿轮的转动惯量;Jm为关节轴的转动惯量;ωm为关节轴的角速度;ic为小齿轮和大齿轮的传动比。
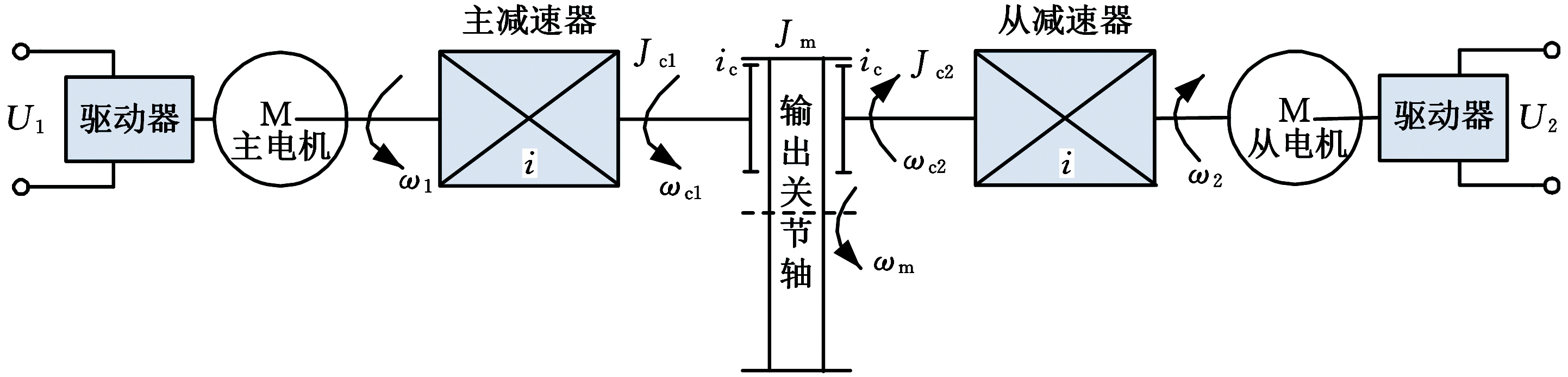
图4 机械臂俯仰关节(2,3,5)双电机系统结构简图
Fig.4 Dual-motor system structure diagram of manipulator pitch joints(2,3,5)
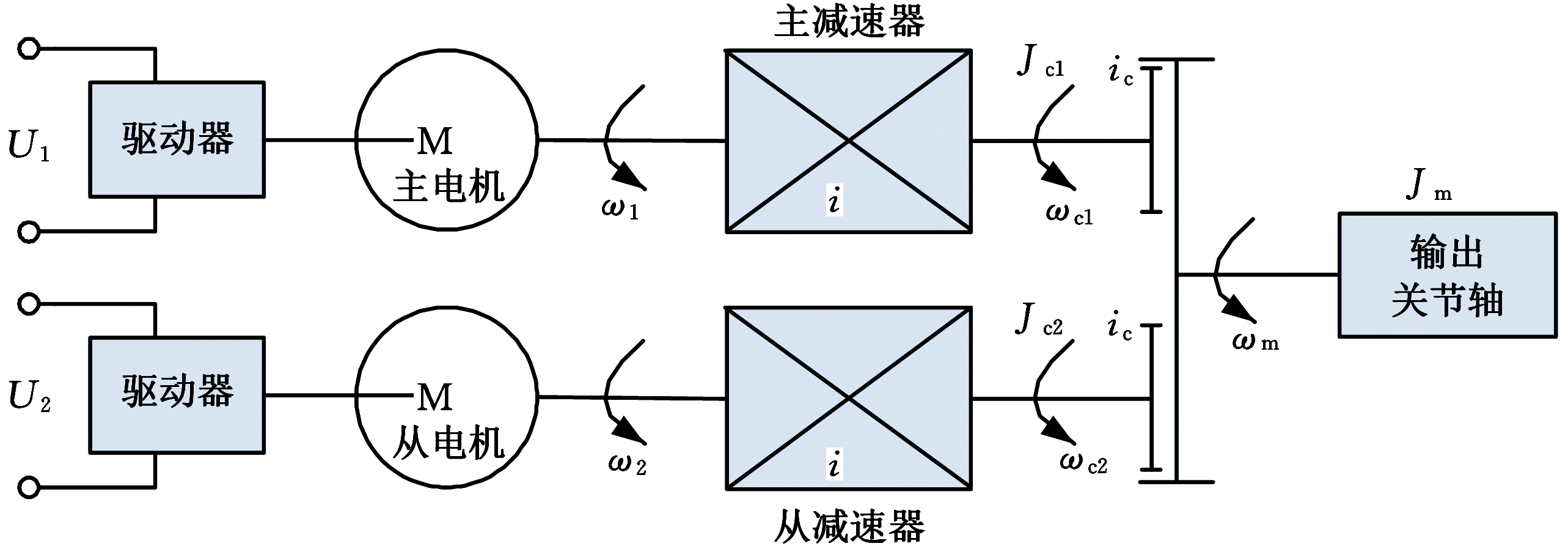
图5 机械臂扭转关节(1,4)双电机系统结构简图
Fig.5 Dual-motor system structure diagram of manipulator twisting joints(1,4)
2.3 系统仿真模型的建立
双电机消隙有偏置力矩补偿控制、基于位置偏差补偿控制、基于速度偏差补偿控制等多种方法,但由于每个电机通过各自减速器耦合至大齿轮盘,再通过大齿轮盘带动关节转动,该连接为刚性连接,通过位置或速度偏差容易激发差速振荡而影响系统稳定性,故本系统采用基于恒偏置力矩的主从控制。
与一般的伺服控制不同,主从双电机消隙驱动控制采用一个扭矩补偿控制器为主从轴提供偏置扭矩,同时对主从轴速度控制器反馈的速度输出值iset以及张力扭矩的设定值进行计算,并将其计算输出值VA实时传递到主从轴上,与位置控制器的输出值Vset叠加后作为速度环的设定输入,这样就保证了从动轴获得的速度指令在任何情况下都能与主动轴保持协调一致,从而实现了2个伺服电机的协调运行,避免出现所谓“伺服打架”现象,如图6所示[8-11]。
由算法原理框图(图6),结合图4、图5,推导含齿隙双电机驱动系统的动力学关系如下:
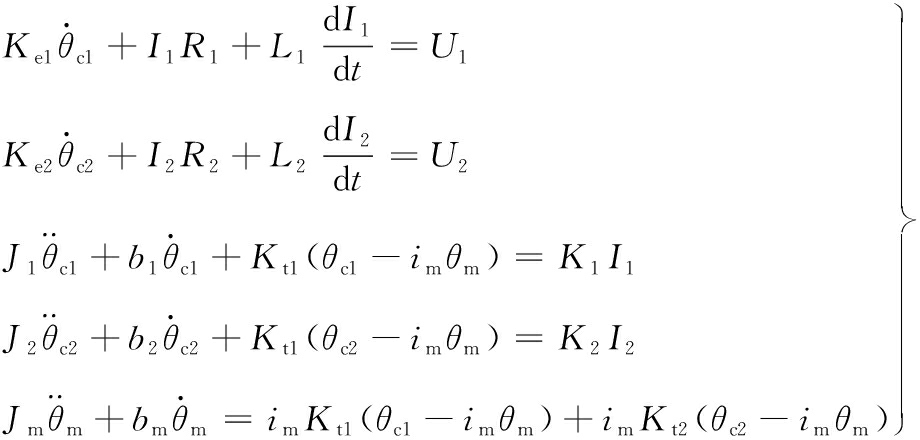
(2)
式中,I1(2)、R1(2)、L1(2)分别为双电机电枢回路的电流、电阻和电感;Ke1(e2)为双电机的反电势系数;θc1(c2)为双电机转角;θm为大齿轮转角;im为大齿轮传动比;J1(2)为双电机转动惯量;b1(2)为双电机等效黏性摩擦系数;K1(2)为双电机传动力矩系数;Kt1(t2)为双电机传动轴弹性系数。
将式(2)进行拉氏变换,得
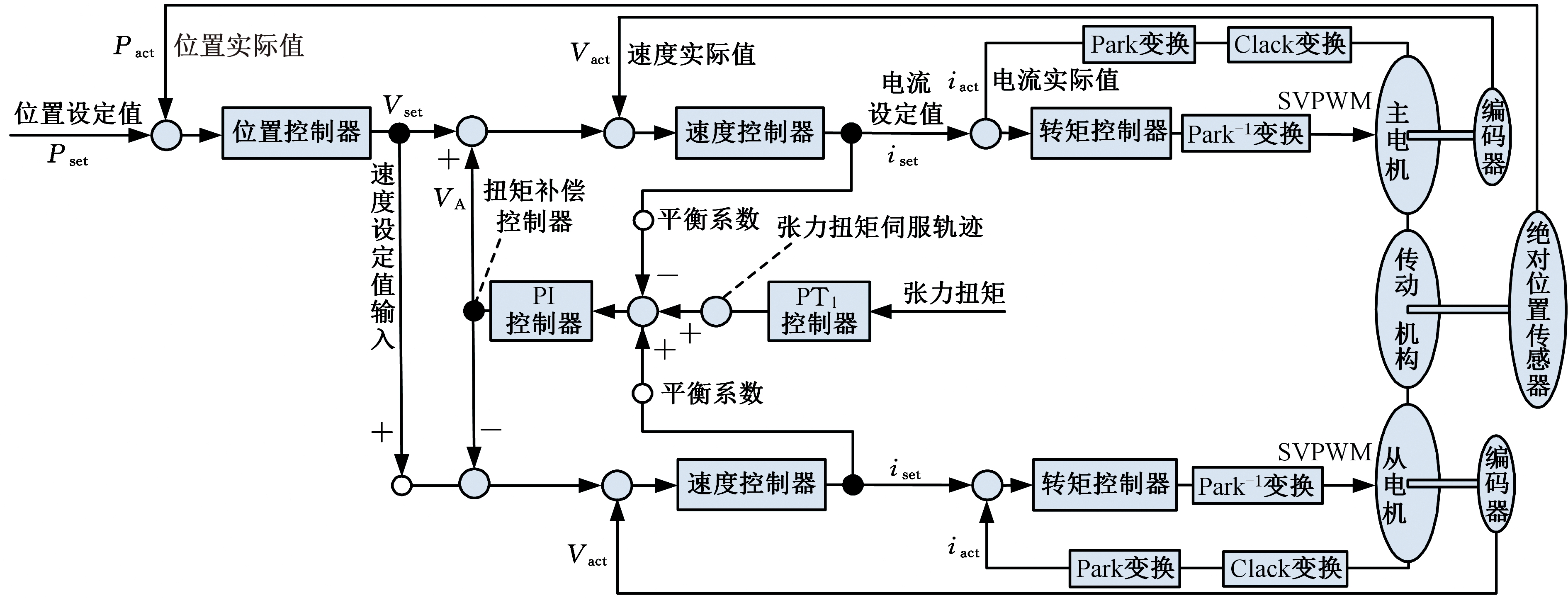
图6 双电机主从消隙驱动控制算法原理图
Fig.6 Anti-backlash drive control algorithm schematics of dual-motor master-slave drivers
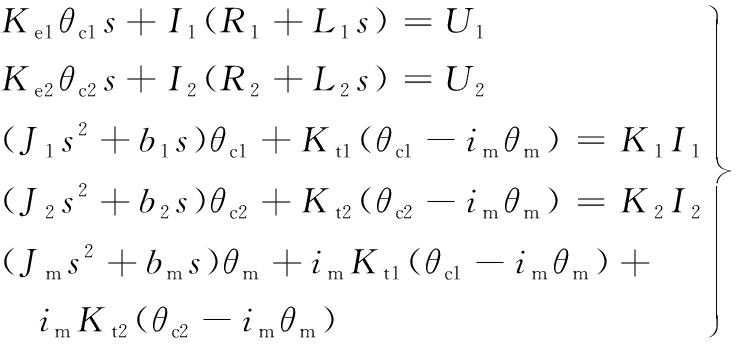
(3)
在此基础上添加位置环及速度环PID控制器、偏置扭矩控制器及滤波函数,建立本文所述系统的复数域仿真框图,如图7所示。
本文系统的仿真参数采用机械臂关节2的选用参数,详细见表1。
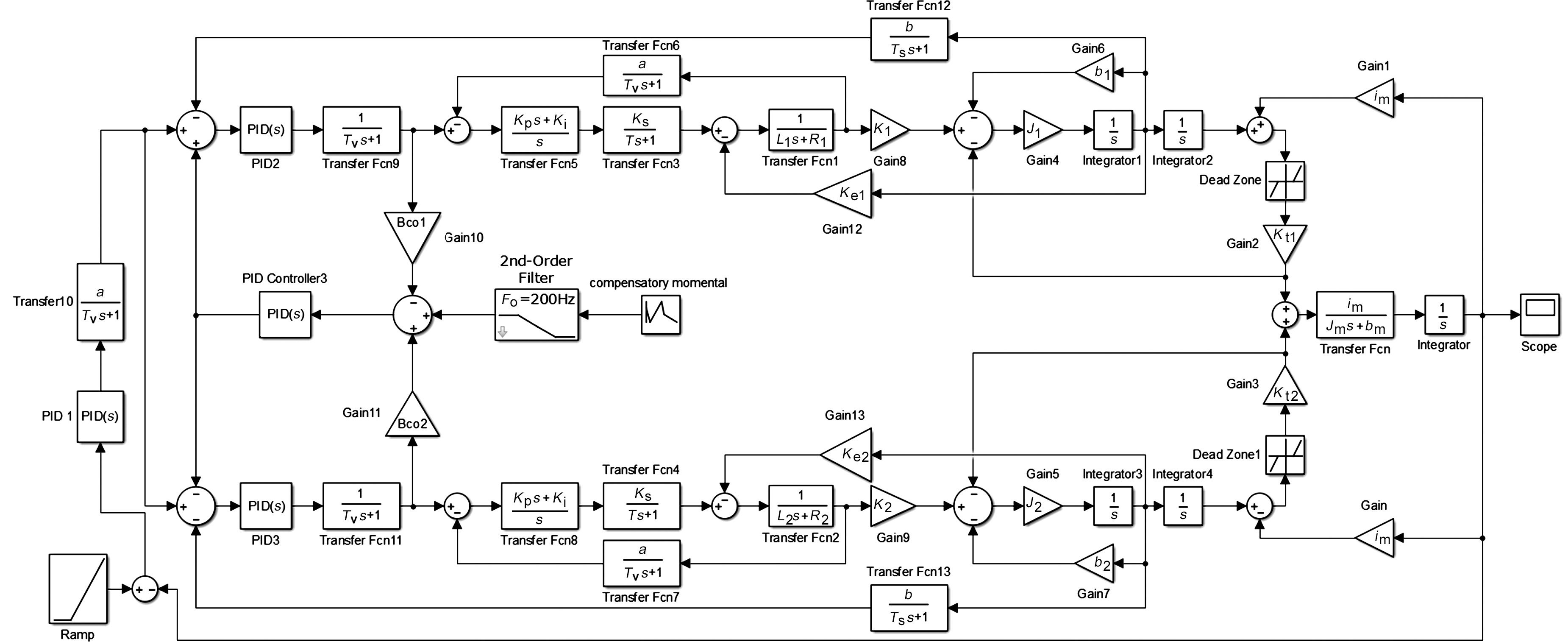
图7 双电机主从消隙驱动Simulink模型
Fig.7 Simulink model of dual-motor master-slave anti-backlash drivers
表1 机械臂关节2设计元部件选用参数
Tab.1 Design components selected parameters ofmanipulator joint 2
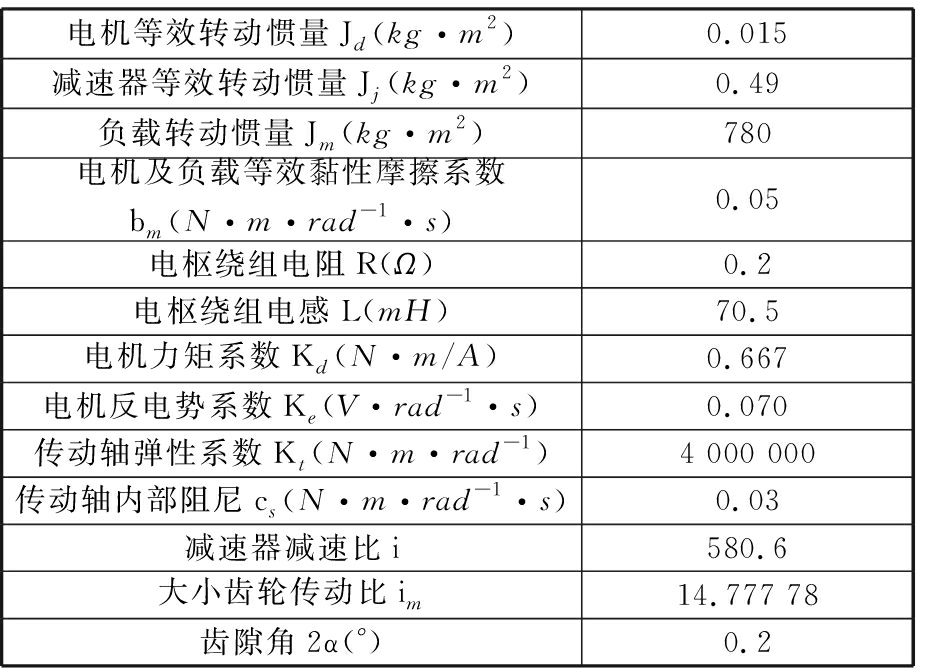
电机等效转动惯量Jd(kg·m2)0.015减速器等效转动惯量Jj(kg·m2)0.49负载转动惯量Jm (kg·m2)780电机及负载等效黏性摩擦系数bm(N·m·rad-1·s)0.05电枢绕组电阻R(Ω)0.2电枢绕组电感L(mH)70.5电机力矩系数Kd(N·m/A)0.667电机反电势系数Ke (V·rad-1·s)0.070传动轴弹性系数Kt(N·m·rad-1)4 000 000传动轴内部阻尼cs(N·m·rad-1·s)0.03减速器减速比i580.6大小齿轮传动比im14.777 78齿隙角2α(°)0.2
2.4 系统仿真结果
在MATLAB的Simulink环境下对双电机驱动系统进行仿真。初始时刻小齿轮参与啮合的轮齿均位于大齿轮齿槽中位,即初始时刻轮齿未啮合。电流环及速度环选择PI控制,位置环选择PID控制。分别在两台电机的电流给定处(速度环输出处)提取电流值作差,并与给定的偏置电流进行比较,将比较结果耦合到两台电机的速度环给定值中,通过转速偏差间接调节电机的补偿力矩值。仿真参数:位置环kP=0.8、kI=0.5、kD=0.1;速度环kP=0.55,kI=0.2,以主动轮侧为参照的齿隙角2α=0.2°,其他设计基本参数不变(表1)。滤波器常数TV =0.001, TS=0.001。位置环的给定输入为斜坡形,测试输出响应,如图8两条曲线所示,位置角度能够跟踪斜坡响应;测试偏置转矩预加载过程,位置环给定为零,如图9所示,约0.3 s后,角差和约为0.2°,完成预加载过程。主动轮1、2 逐渐与从动轮紧密啮合,两个主动轮始终与从动轮保持紧密啮合,验证了双电机消隙技术的可行性。
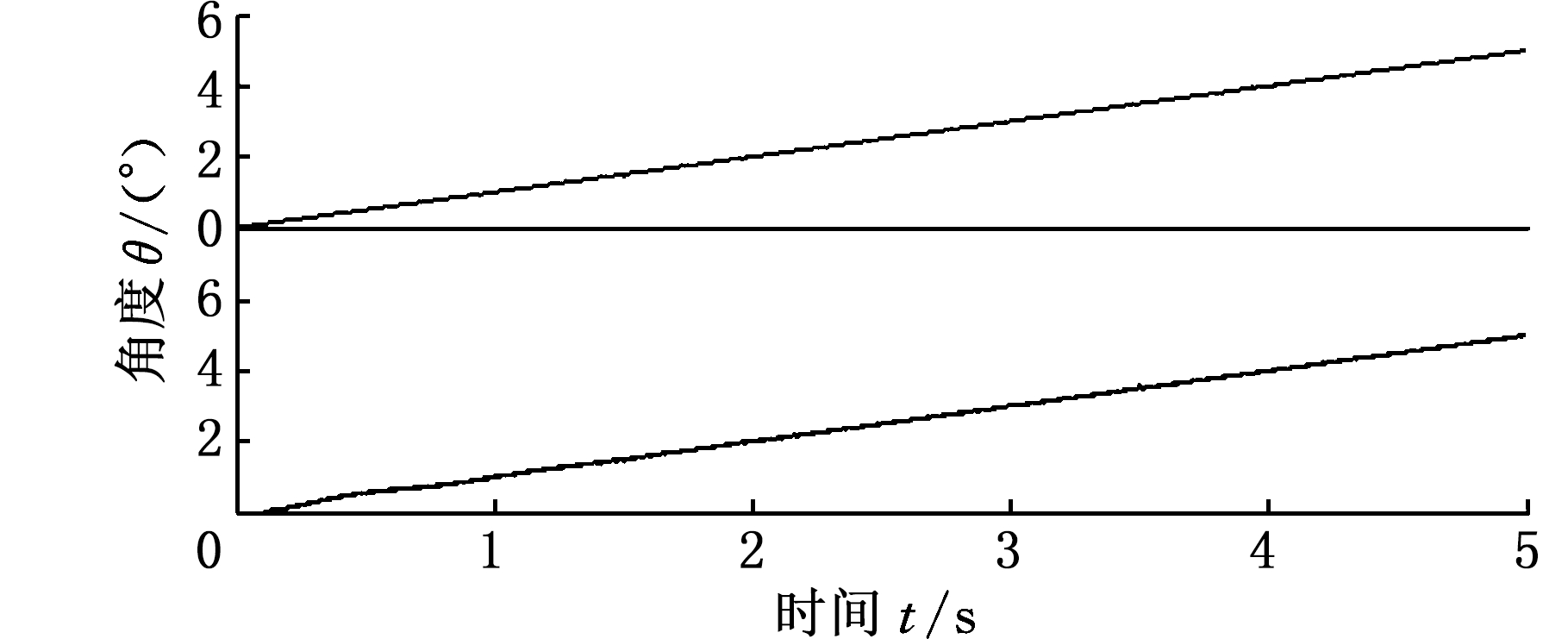
图8 输出轴斜坡响应仿真结果
Fig.8 The output shaft simulation results of ramp response
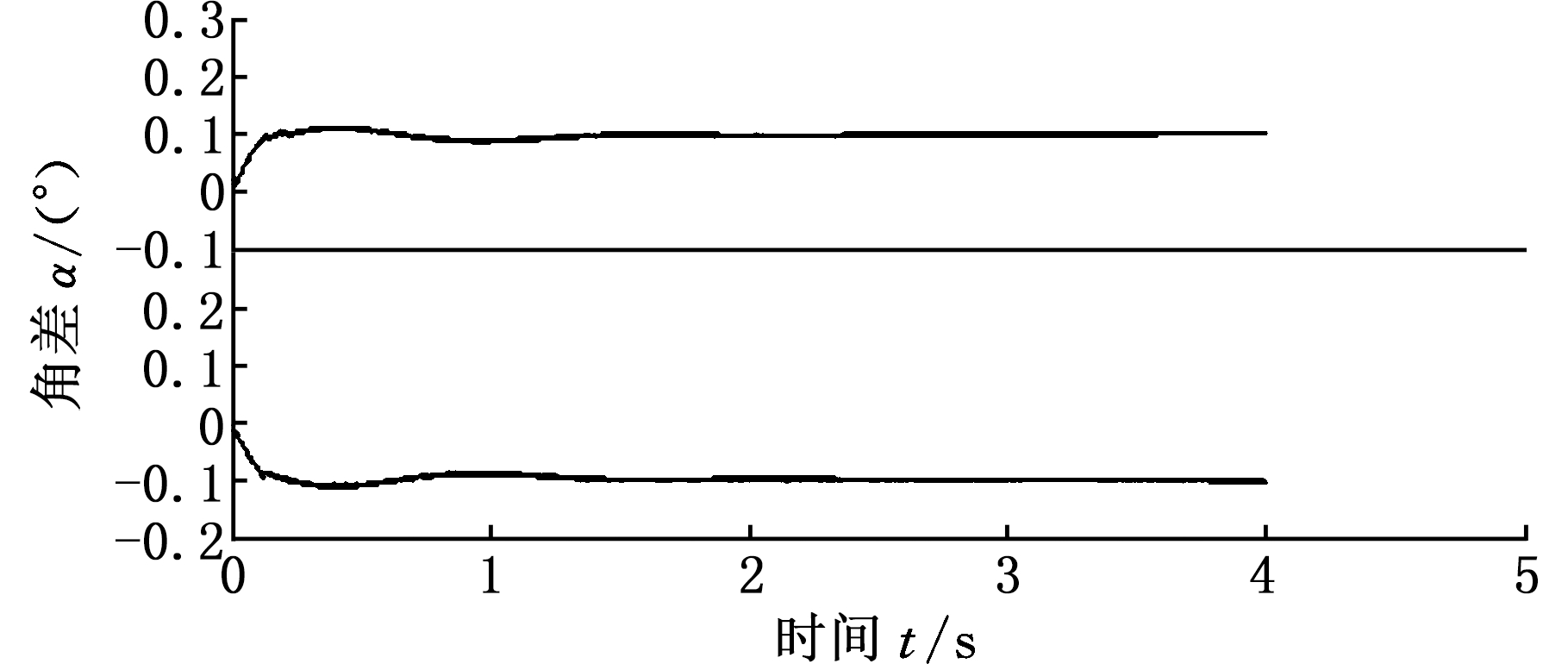
图9 预加载过程中角差仿真结果
Fig.9 Angle difference simulation results of
preloading process
3 双电机主从驱动消隙技术的实现
本文的主从驱动消隙技术设计方案采用DSP数字处理器+IR2136驱动逆变桥的方法实现,将TMS320F28335的高速浮点数字信号处理功能和IR2136高度集成的电平转换技术完善结合。硬件电路基本工作原理如图10所示:与从驱动器相比,各关节主驱动器外接关节位置传感器完成与上位机之间报文交互;各关节的主驱动器接收上位机通过整臂RS422总线下发的位置指令,经位置环及扭矩补偿算法的控制运算,将偏置转矩转发给从驱动器,使双电机协同工作;模拟电路模块将永磁同步电机(PMSM)相电流信号转化为ADC的输入信号,转换后的采样数据送到DSP进行分析,Park变换、Clark变换等一系列正反变换完成电流环PI控制,根据定子与转子之间的电角度,以SVPWM形式驱动逆变桥使电机定子形成平滑的直流磁场。
为验证双电机主从消隙技术的合理性,同时避免直接调试机械臂可能带来的对人身及设备的危险,搭建了技术验证平台,如图11所示,验证平台仿照机械臂关节2选用部件设计。
基于双电机消隙技术实现的机械臂总质量为800 kg,长度为4.7 m,采用灵活易集成的无框电机设计,能在有限的空间内实现双电机消隙传动系统精度的要求。其中,电机母线电压为100 V,最大电流为10 A,自主设计驱动器的电流能满足力矩需求。
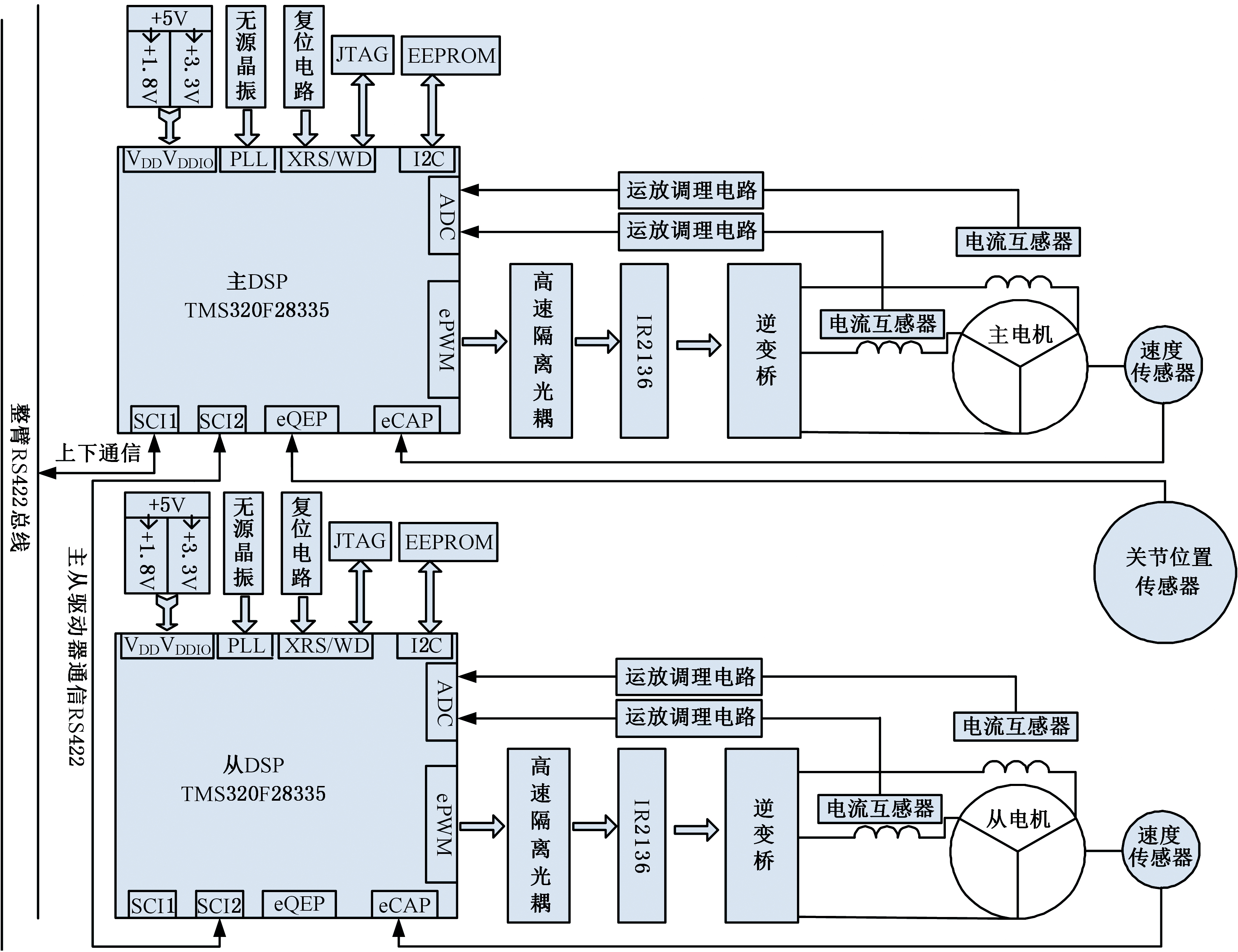
图10 机械臂单关节硬件电路原理框图
Fig.10 Hardware circuit block diagram of manipulator single joint

图11 双电机主从消隙驱动技术验证平台
Fig.11 Verification platform of dual-motor
master-slave driver technology
4 双电机消隙对机械臂的精度提高
本文对工作空间范围在4.5 m内的串联机械臂末端位姿进行精度测试验证[12-13]。测量工具为Leica AT901-LR型激光跟踪仪,该跟踪仪主要由激光头、靶标以及承载激光头的方位、俯仰两个方向的码盘组成。
用激光跟踪仪确定测量机械臂基坐标系在激光跟踪仪坐标系中的位姿为
(4)
式中,R0、P0分别为机械臂基坐标系在激光跟踪仪坐标系中的姿态、位置。
若机械臂末端在其基坐标系中的位姿为T,则机械臂末端位姿的激光跟踪仪测量值TLas为
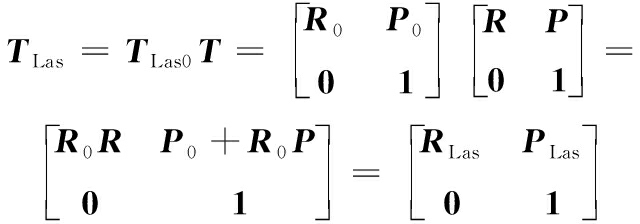
(5)
式中,R、P分别为机械臂末端在其基坐标系中的姿态、位置;RLas、PLas分别为机械臂末端在激光跟踪仪坐标系中的姿态、位置。
所以
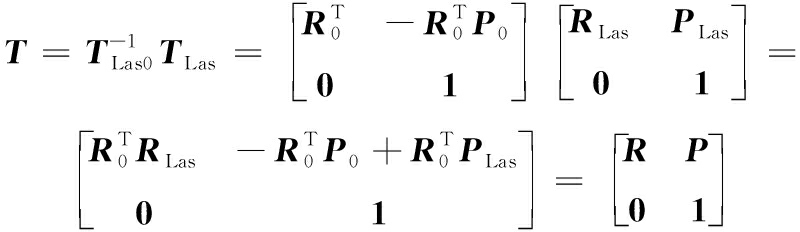
(6)
因此有计算公式:
(7)
利用上述公式,控制机械臂伺服到指令位姿TCMD,然后用激光跟踪仪测量机械臂末端位姿T,比较TCMD与T,得到机械臂的绝对位姿误差。
根据以上精度测量方法,通过机械臂位姿指令使机械臂末端行走一个圆形轨迹,将各点测量结果经软件拟合可得,经双电机消隙后其精度误差约为1.171 mm。
5 结语
与传统的机械消隙法(包括双片薄齿轮错齿调整法、弹簧力偏置法、轴向垫片调整法等)相比,本文方法具有以下优点:机械消隙仅能提高系统静态性能,而双电机消隙能提升系统静动态性能;双电机消隙结构简单,体积更小,且不需要高精度的减速机构;双电机消隙后期维护更简单,同时可以采用两个小驱动容量之和实现大力矩驱动,受磨损、环境的影响非常小。
本文采用双电机伺服驱动消除传动反向间隙的原理来降低串联机械臂各轴频繁反向过程中因反向间隙引入的传动误差和刚度损失,同时有效抑制外部小幅时变干扰,抑制齿轮传动刚度的时变性、齿轮加工偏心度等引起的时变干扰,能够从根本上提高机械臂动态性能及精度指标。经技术应用验证,工作空间为4.5 m的串联机械臂采用双电机主从驱动消隙技术后精度误差约为1.171 mm。
[1] ANTONIO B, ALFONSO B. Input-Output Stability of Systems with Backlash[J]. Automatica, 2006,42:1017-1024.
[2] CAZAREZCASTRO N R , AGUILAR L T, CASTILLO O. A Fuzzy-genetic Controller for the Output Regulation of a Servomechanism with Backlash[C]∥IEEE Workshop on Hybrid Intelligent Models and Applications. Nashville, 2009:11-16.
[3] KOREN Y.Cross-coupled Biaxial Computer Control for Manufacturing System[J].ASME Journal of Dynamic Systems,Measurement and Control,1980,102(12):256-272.
[4] TOMIZUKA M,HU J,CHIU T,et al.Synchronization of Two Motion Control Axes under Adaptive Feedforward Control[J].ASME Journal of Dynamic Systems,Measurement and Control,1992,114(6):196-203.
[5] SRINIVASAN K, KULKARNI P.Cross-couple Control of Biaxial Feed Drive Servomechanism[J]. ASME Journal of Dynamic System, Measurement and Control, 1990, 112(6):225-232.
[6] 陈庆伟,郭毓,胡维礼,等.多电机同步联动系统的动力学分析与建模[J].东南大学学报(自然科学版),2004,34(增刊):135-140.
CHEN Qingwei, GUO Yu, HU Weili,et al. Dynamics Analysis and Modeling of Multi-motor Synchronized Driving System[J]. Journal of Southeast University( Natural Science Edition), 2004,34(S):135-140.
[7] 朱国力,龚时华,李斌.七轴五联动螺旋桨加工机床控制系统关键技术[J].华中科技大学学报(自然科学版),2007,35(3) :77-79.
ZHU Guoli, GONG Shihua, LI Bin. Study on Key Technology of Control System for Propeller Processing Machines[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2007,35(3) :77-79.
[8] 汤辉, 吴影生.双电机驱动精密二维测试转台伺服系统设计与实现[J].电子机械工程,2009,25(5):38-40.
TANG Hui, WU Yingsheng. Design and Realization of a Dual-motor Driving Servo System for a 2D Precise Test Turntable[J].Electro-Mechanical Engineering,2009,25(5):38-40.
[9] 刘志兵,孙志强.双电动机消隙驱动在大重型机床上的应用[J].制造技术与机床,2010(4):77-80.
LIU Zhibing,SUN Zhiqiang. Application of Twin Motor Drive Eliminating Backlash on Heavy and Large Machine Tool[J]. Manufacturing Technology & Machine Tool, 2010(4):77-80.
[10] 胡超, 施浒立, 宁春林. 齿轮消隙功能实现探索[J]. 机电工程, 2008,25(2):11-14.
HU Chao, SHI Huli, NING Chunlin. Research onFunctional Implementation of Gear Clearance Eliminating[J].Mechanical & Electrical Engineering Magazine, 2008,25(2):11-14.
[11] 赵国峰,胡维礼. 双电机驱动伺服系统齿隙非线性控制研究[J].电气传动,2005, 35(3) :24-27.
ZHAO Guofeng,HU Weili. Backlash Nonlinearity Control of Servo System Driven by Two Motors[J]. Electric Drive, 2005, 35(3) :24-27.
[12] CHEN Xiaorong,CAI Ping,SHI Wenkang,et al.Dynamic Measuring the Position of a Moving Object Based on Laser Tracking System[J]. Chinese Journal of Scientific Instrument, 2004, 25(6): 777-8191.
[13] 刘伟,赵剑波,高峰,等.基于相对坐标的机器人末端位姿测量方法[J].机器人,2009,31(1):15-19.
LIU Wei, ZHAO Jianbo, GAO Feng,et al. Pose Measurement of Robot Based on Relative Coordinate[J]. Robot,2009,31(1):15-19.
