0 引言
球度误差的快速、精确评定对球类零件合格性的判定非常重要。目前,球度误差没有统一的评定标准,但可从圆度误差评定模型[1-2]扩展得出球度误差定义:包容实际球轮廓的半径差为最小的同心球半径差。球度误差的评定方法主要有四种:最小二乘法、最小外接球法、最大内接球法、最小包容区域法[3]。最小包容区域法符合球度误差定义中的最小条件,得到的球度误差为唯一最小值,也是球度误差评定出现不一致时的仲裁方法,但其属于无约束非线性化问题,利用计算机对其直接求解非常困难。
关于基于最小包容区域法的球度误差评定算法已有很多研究成果:区域搜索法[4-5]、仿生智能优化算法[6-9]、按数学算法或计算几何方法对采样点进行筛选的方法[10-12]、利用采样点和球心位置的几何关系来调整球心位置直至满足条件的方法[13-16]。这些方法都可以得到比最小二乘法评定更精确的结果,但区域搜索法存在原理误差,不能得到球度误差的精确解;仿生智能优化算法存在参数调整的难题;计算几何和利用采样点调整球心位置方法的数学模型复杂、理论深奥,还需要大量的计算。因此,它们的应用在一定程度上受到了限制。
针对现有方法模型复杂且不能准确得到最小包容区域球度误差的缺点,笔者提出一种将几何搜索逼近算法与球度误差最小包容区域法的几何结构和定义结合起来的球度误差评定方法。该方法原理简单,符合球度误差定义,得到的结果为球度误差的精确解且具有很好的稳定性。
1 球度误差最小包容区域法评定模型
1.1 球度误差最小包容区域评定的目标函数
根据球度误差定义可得球度误差最小包容区域评定的目标函数:
f=max|(xi, yi, zi)-(x0, y0, z0)|-
min|(xi, yi, zi)-(x0, y0, z0)|
(1)
式中,f为最小包容区域球度误差;(xi, yi, zi)为采样数据点Pi的坐标,i=1,2,…,n;(x0, y0, z0)为最小包容区域球的球心坐标。
由式(1)可知,球度误差最小包容区域评定属于无约束非线性化问题,直接对其求解非常困难。
1.2 球度误差最小包容区域评定的几何结构
利用最小包容区域法进行球度误差评定的几何结构为“3+2”形式和“2+3”形式[16],但球度误差只有唯一最小值,因此,最小包容区域球度误差为:利用两种几何结构分别进行球度误差评定所得结果中的最小值,即
F=min(f3+2, f2+3)
(2)
其中,fa+b为“a+b”形式的最小包容区域球度误差,a为同心球外球上的点数,b为同心球内球上的点数,文中将外球上a个点和内球上b个点称为控制点。所有的采样点都被包含在a+b个控制点确定的同心球内外表面之间的区域内,球度误差为2个同心球的半径差。
1.3 几何结构对应的同心球球心坐标的确定
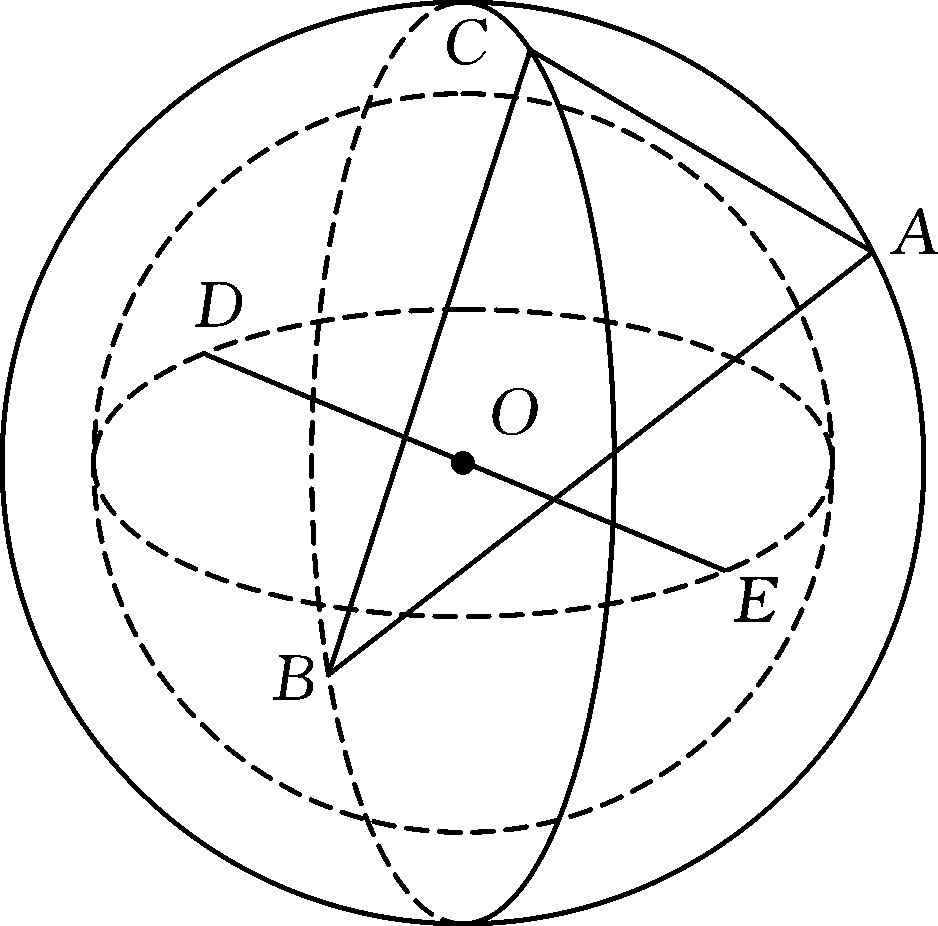
图1 “3+2”形式球度误差最小包容区域评定的几何结构
Fig.1 “3+2” form geometry of sphericity evaluation based on minimum coverage area
“3+2”形式的球度误差最小包容区域评定几何结构如图1所示。根据几何知识可知:过三角形外心且垂直于三点确定的平面的直线到3个点的距离相等;两点之间线段的中垂面上的点到线段两端距离相等;直线与中垂面的交点为最小包容区域球的球心。图1中,由点A(xA, yA, zA)、B(xB, yB, zB)和C(xC, yC, zC)确定的过△ABC外心且垂直于△ABC平面的直线公式为
(x-xA)2+(y-yA)2+(z-zA)2=
(x-xB)2+(y-yB)2+(z-zB)2=
(x-xC)2+(y-yC)2+(z-zC)2
(3)
点D(xD, yD, zD)、E(xE, yE, zE)间线段的中垂面公式为
(x-xD)2+(y-yE)2+(z-zD)2=
(x-xE)2+(y-yE)2+(z-zE)2
(4)
联立式(3)、式(4)可得到由外球控制点A、B、C与内球控制点D、E确定的球度误差最小包容区域评定所得的同心球球心坐标:

(5)
“2+3”形式的球度误差最小包容区域评定的几何结构如图2所示。同理,由图2可得到由外球控制点F、G与内球控制点H、I、J确定的球度误差最小包容区域法评定所得的同心球球心坐标:
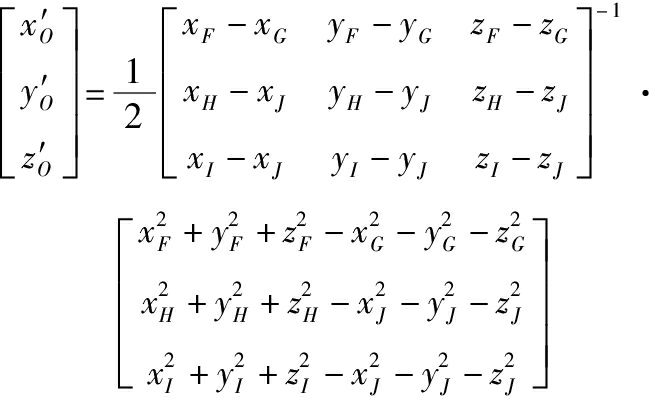
(6)
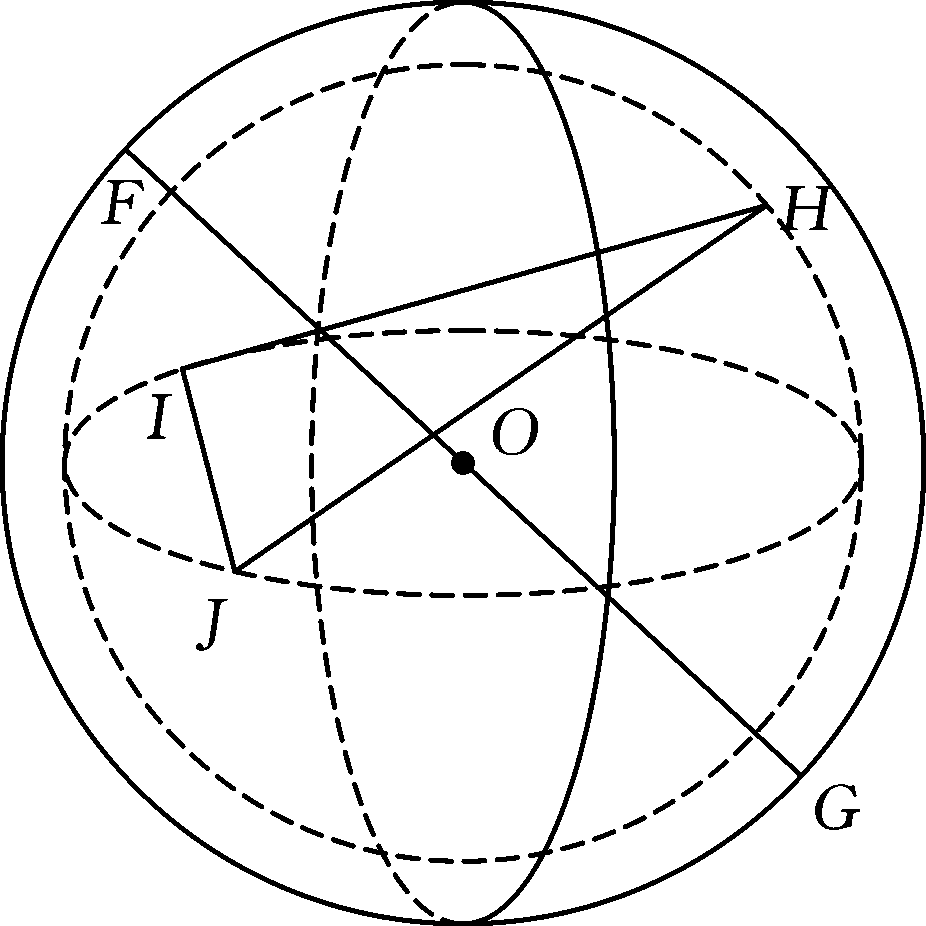
图2 “2+3”形式球度误差最小包容区域评定的几何结构
Fig.2 “2+3” form geometry of sphericity evaluation based on minimum coverage area
2 评定方法及步骤
首先,使用最小二乘法计算得到最小二乘球心和最小二乘误差。其次,在以最小二乘球心为初始球心、以最小二乘误差为初始半径的球内进行几何搜索逼近,确定准球心位置。然后,由准球心和球度误差最小包容区域法的几何结构来确定外球上和内球上的点,依据球度误差的最小包容区域法定义判断当前得到的点是否符合要求,若不符合,则按照选取当前最近点或减小几何搜索逼近算法的阈值等规则进行调整;若符合,则当前点即为控制点。最后,将控制点坐标先后代入式(5)(“2+3”形式则代入式(6))和式(1),计算得出球心和球度误差。两种形式球度误差的最小值为最小包容区域球度误差。
2.1 f3+2最小包容区域法评定
2.1.1 确定初始参考点
根据采样点Pi的坐标,采用线性化最小二乘法得到最小二乘球心OLS(xo,yo,zo)、最小二乘半径RLS的计算公式如下:
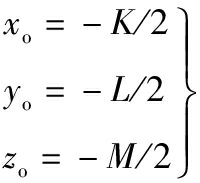
(7)
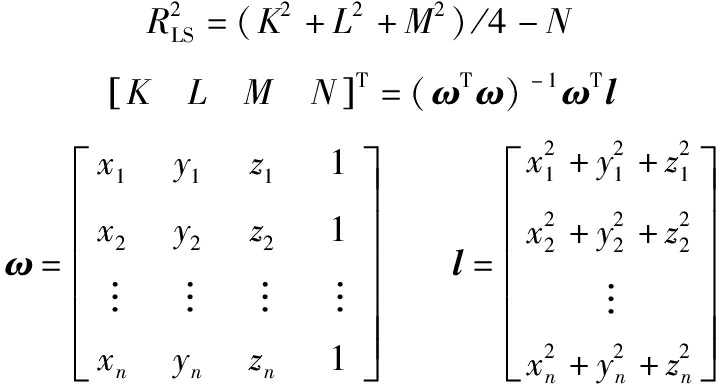
将(xo, yo, zo)代入式(1),可得最小二乘球度误差vLS。
2.1.2 几何搜索逼近准球心位置
最小包容区域球心在以最小二乘球心为球心、最小二乘球度误差为半径的球内。采用几何搜索逼近来获取准球心位置,首先设置以(xo, yo, zo)为球心、vLS为半径的初始搜索球。为了表述方便,用O0表示搜索球球心,E0表示O0对应的球度误差,可知初始的O0=OLS,E0=vLS。
搜索球表面有14个点(坐标轴与球面的6个交点、搜索球内接正方体的8个顶点)。依次将14个点作为假定最小包容区域球心,根据式(1)计算与这14个点对应的包容采样点的同心球半径差值,该同心球半径差值中的最小值用Emin表示。
Emin≥E0说明搜索球球心O0更接近最小包容区域球心,则搜索球的球心不变,半径改变为原来的1/2;Emin<E0说明Emin对应的点Omin更接近最小包容区域球心,则将Omin作为搜索球的球心,在新的搜索球内,按原半径重新计算E0和Emin。
重复上述步骤,直到搜索球的半径小于某个阈值(初始值设为vLS/1 000),则认为搜索球的球心很接近最小包容区域球心,将此时搜索球的球心作为准球心Oq(xq, yq, zq)。
2.1.3 确定外球上3个点和内球上2个点
计算采样点Pi到准球心Oq的距离,首先找出距离最大的3个点Q(xQ, yQ, zQ)、S(xS, yS, zS)、T(xT, yT, zT)和距离最小的点U(xU, yU, zU)作为外球上的3个点和内球上的第一个点。然后依次将其余采样点作为假定内球上的第二个点,判断此点与Q、S、T和U组成的5个点是否满足“3+2”形式的几何结构,若不满足,则此点不符合要求;若满足,则先用式(5)计算当前5个点确定的同心球球心,再将球心坐标代入式(1)计算此球心对应的包容采样点的同心球半径差值。每个满足要求的采样点都对应一个同心包容球的半径差值,将这些半径差值中的最小值对应的采样点作为内球的第二个点V(xV, yV, zV)。
2.1.4 确定控制点
将点Q、S、T、U、V的坐标代入式(5)可确定同心球的球心OW(xW, yW, zW)、内半径RU、外半径RQ:
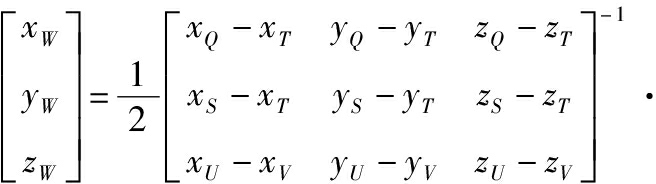
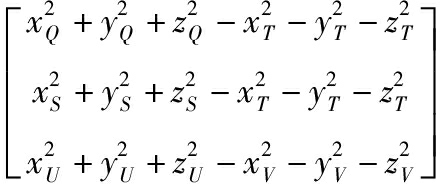
RU=|(xU, yU, zU)-(xW, yW, zW)|
RQ=|(xQ, yQ, zQ)-(xW, yW, zW)|
采样点Pi到OW的距离di的最小值用dMIN表示,dMIN对应的采样点为PMIN(xMIN, yMIN, zMIN),最大值用dMAX表示,dMAX对应的采样点为PMAX(xMAX, yMAX, zMAX)。
为了判断当前同心球是否满足球度定义,首先比较dMIN和RU,dMIN<RU说明有采样点落在当前同心球的内球表面之内,那么用点PMIN代替点U,执行2.1.3节所述的过程,调整同心球内球上的控制点位置,从而调整当前同心球的内球轮廓,使得没有采样点位于内球表面内部;dMIN≥RU说明所有点都落在同心球内球表面之外。然后比较当前的dMAX和RQ,dMAX>RQ说明有采样点位于当前同心球的外球表面之外,执行2.1.2节所述的过程,调整同心球外球上控制点位置,使所有采样点位于其表面之内,且将几何搜索逼近算法的阈值设为原来的1/2;dMAX≤RQ说明采样点都落在当前同心球外球表面之内,当前得到的5个采样点即为符合“3+2”形式的球度误差的最小包容区域法评定的控制点。
2.1.5 计算球心坐标和球度误差
对确定的5个控制点,利用式(5)得出同心球球心坐标;将球心坐标代入式(1)可得出f3+2。图3为f3+2最小包容区域法评定的MATLAB程序流程图。
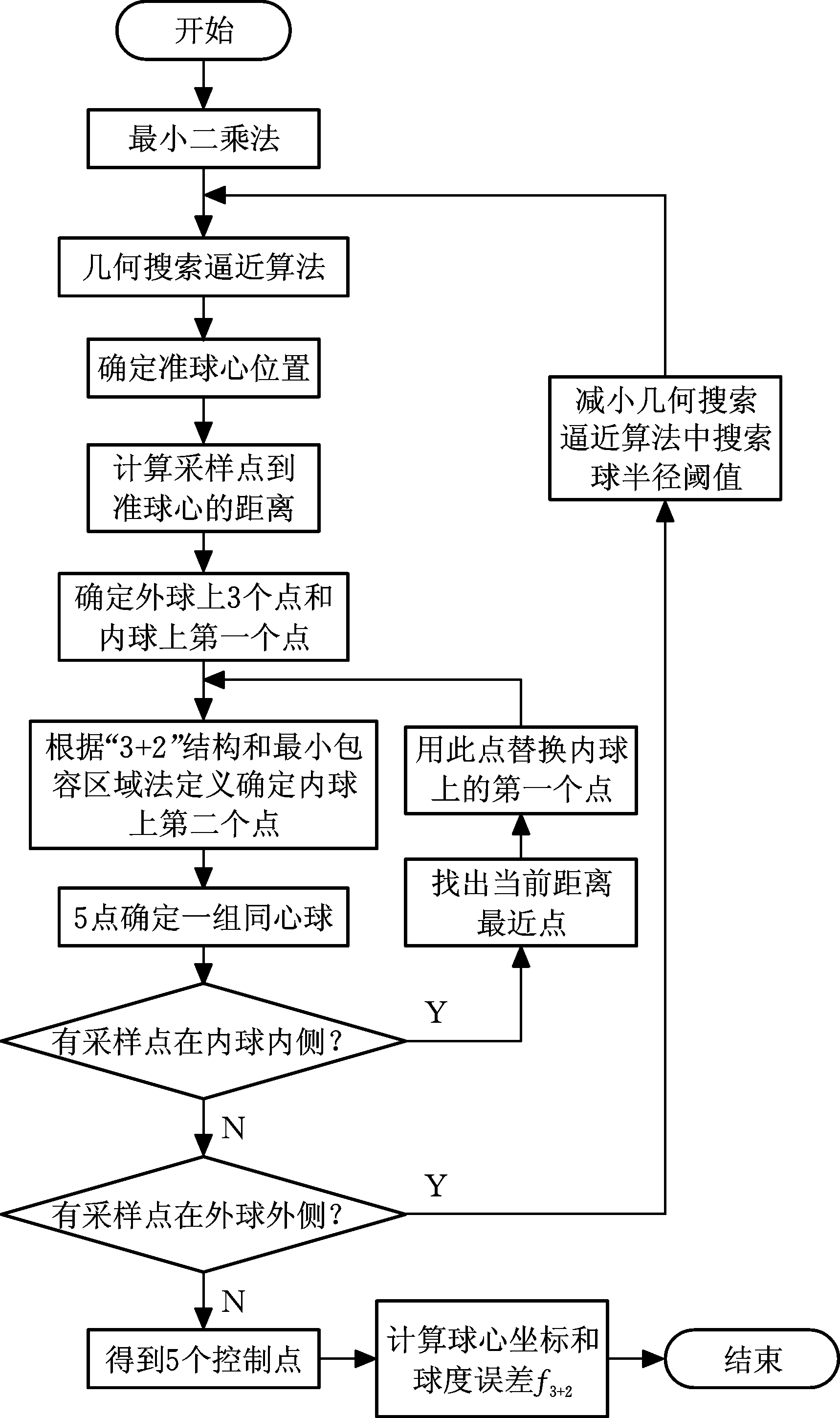
图3 f3+2最小包容区域评定程序流程图
Fig.3 Flow chart of f3+2 evaluation based on minimum coverage area
2.2 f2+3最小包容区域法评定
采用2.1.1节方法确定初始参考点和最小包容区域球心所在范围,采用2.1.2节方法确定准球心位置。
2.2.1 确定外球上2个点和内球上3个点
计算所有采样点到准球心的距离,将距离最大和次大的2个点作为当前同心球外球上的点,分别记为q(xq, yq, zq)、s(xs, ys, zs);将距离最小和次小的2个点作为当前同心球内球上的点,分别记为t(xt, yt, zt)、u(xu, yu, zu)。同心球的外球半径受球心变化影响小,相对容易求得,故先确定外球上控制点的位置[13]。然后依次将q、s、t和u之外的采样点作为假定内球上的点,判断其与q、s、t和u组成的5个点是否符合“2+3”形式的几何结构,若不满足,则此点不符合要求;若满足,则先用式(6)计算当前5个点确定的同心球球心,再将球心坐标代入式(1)计算此球心对应的包容采样点的同心球半径差值,那么每个满足要求的采样点都会对应一个同心包容球的半径差值,将这些半径差值中的最小值对应的采样点作为内球上第三个点v(xv,yv,zv)。
2.2.2 确定控制点
将点q、s、t、u和v的坐标代入式(6)确定同心球的球心Ow(xw, yw, zw)、内径Ru、外径Rq:
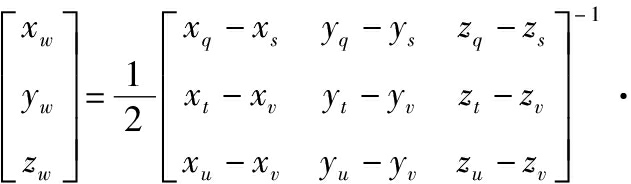
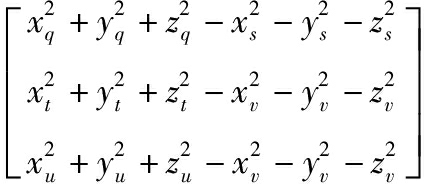
Ru=|(xu, yu, zu)-(xw, yw, zw)|
Rq=|(xq, yq, zq)-(xw, yw, zw)|
计算采样点Pi到Ow的距离di的最小值用dmin表示,dmin对应的采样点为Pmin(xmin, ymin, zmin),最大值用dmax表示,dmax对应的采样点为Pmax(xmax, ymax, zmax)。
为了判断当前同心球是否满足球度的定义,首先比较dmin和Ru,dmin<Ru说明有采样点落在当前同心球的内球表面之内,用点Pmin代替点u,执行2.2.1节所述过程,调整同心球内球上的控制点位置,从而调整同心球内球的轮廓,使得满足所有采样点位于当前同心球内球表面之外的要求;dmin≥Ru说明所有点都落在同心球的内球表面之外。然后比较当前的dmax和Rq,dmax>Rq说明有采样点位于当前同心球的外球表面之外,执行2.1.2所述过程,将几何搜索逼近算法的阈值设为原来的1/2,以调整同心球外球使其满足所有采样点位于其表面之内的要求;dmax≤Rq说明采样点都落在当前同心球的外球表面之内,那么当前得到的5个采样点即为符合“2+3”形式的球度误差的最小包容区域法评定的控制点。
2.2.3 计算球心坐标和球度误差
对确定的5个控制点,利用式(6)可得出同心球球心坐标;将球心坐标代入式(1)可得出“2+3”形式最小包容区域法评定的球度误差f2+3。图4为f2+3最小包容区域法评定的程序流程图。最小包容区域球度误差按照式(2)即可求得。
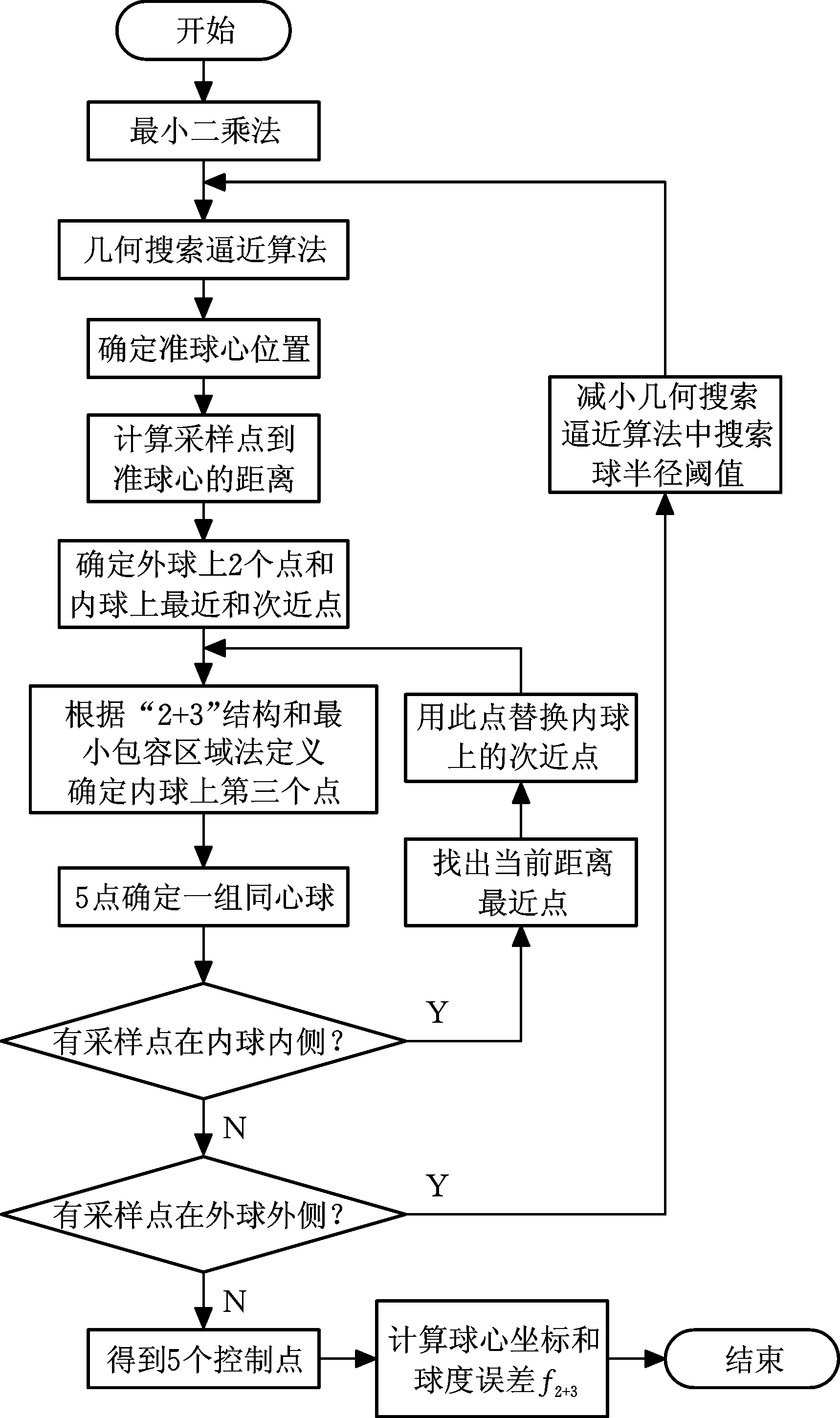
图4 f2+3最小包容区域评定程序流程图
Fig.4 Flow chart of “2+3” evaluation based on minimum coverage area
3 仿真及实例验证
3.1 仿真验证
构造一组已知球度误差的数据来验证本文所述的球度误差最小包容区域评定方法的正确性。这组构造的采样点数据随机分布在以(0,0,0)为球心、外球半径100 mm和内球半径99 mm的球面之间,构造数据的坐标如表1所示。利用排列组合方法,通过比较这些数据所有可能组合对应的亚微米级球度误差,得出这组数据符合最小包容区域法定义的球度误差为1 mm,对应的几何结构为“3+2”形式,其中,外球上控制点序号为1、34、41,内球上控制点序号为15、23。
对构造的采样点数据分别利用最小二乘法(LSM)、粒子群算法(PSO)和本文提出的方法进行处理。粒子群算法采用的是自适应权重粒子群算法,参数设置如下:种群个数为40,惯性权重为0.6~0.9,学习因子c1=c2=2,循环次数为300。数据处理的结果如表2所示。
表1 构造数据的坐标
Tab.1 The coordinates of constructing data mm
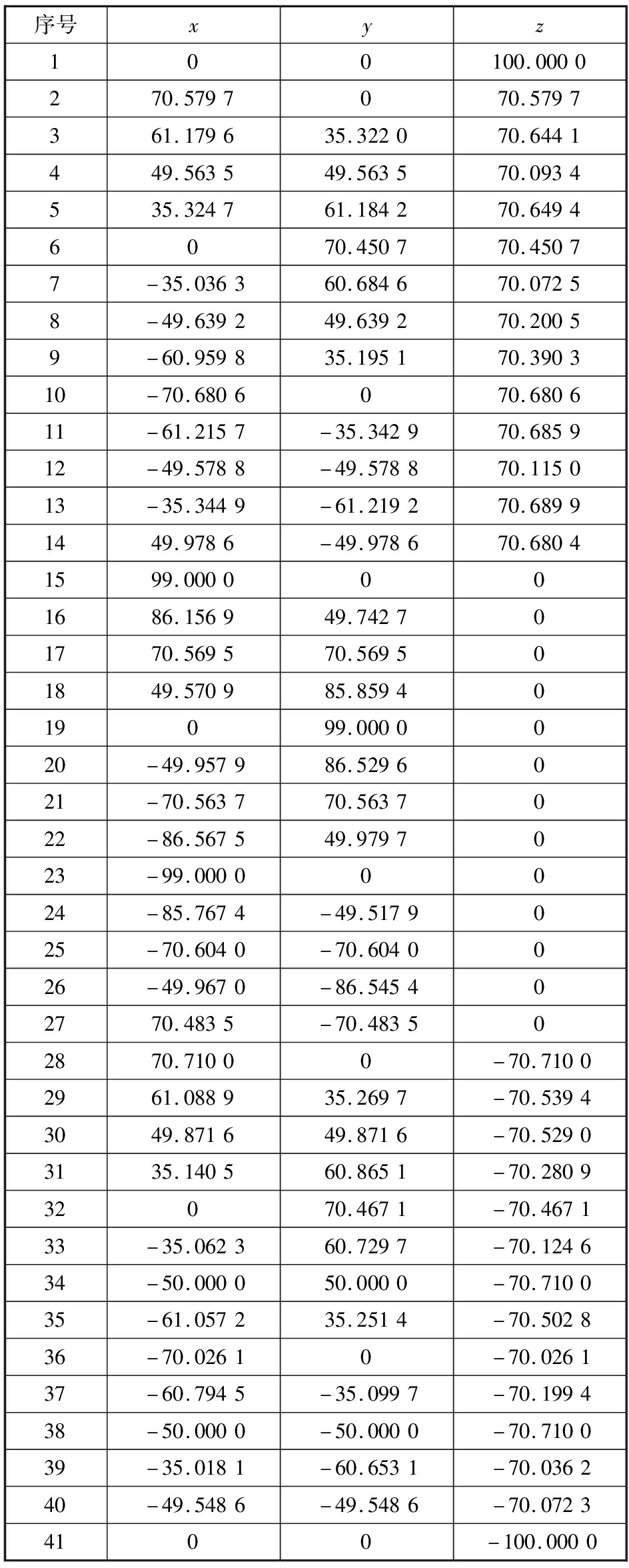
序号xyz100100.0000270.5797070.5797361.179635.322070.6441449.563549.563570.0934535.324761.184270.64946070.450770.45077-35.036360.684670.07258-49.639249.639270.20059-60.959835.195170.390310-70.6806070.680611-61.2157-35.342970.685912-49.5788-49.578870.115013-35.3449-61.219270.68991449.9786-49.978670.68041599.0000001686.156949.742701770.569570.569501849.570985.8594019099.0000020-49.957986.5296021-70.563770.5637022-86.567549.9797023-99.00000024-85.7674-49.5179025-70.6040-70.6040026-49.9670-86.545402770.4835-70.483502870.71000-70.71002961.088935.2697-70.53943049.871649.8716-70.52903135.140560.8651-70.280932070.4671-70.467133-35.062360.7297-70.124634-50.000050.0000-70.710035-61.057235.2514-70.502836-70.02610-70.026137-60.7945-35.0997-70.199438-50.0000-50.0000-70.710039-35.0181-60.6531-70.036240-49.5486-49.5486-70.07234100-100.0000
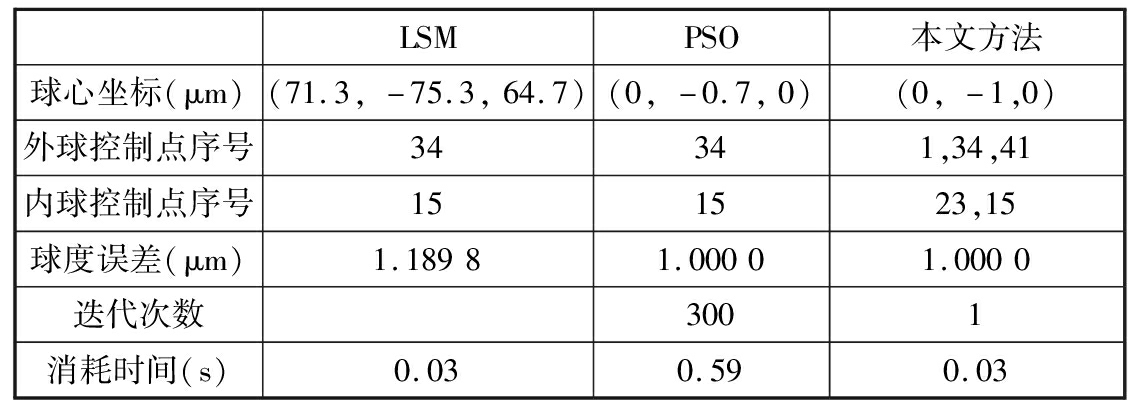
表2 数据处理结果
Tab.2 Results of data processing
LSMPSO本文方法球心坐标(μm)(71.3,-75.3,64.7)(0,-0.7,0)(0,-1,0)外球控制点序号34341,34,41内球控制点序号151523,15球度误差(μm)1.18981.00001.0000迭代次数3001消耗时间(s)0.030.590.03
考虑到实际应用,将球心坐标和球度误差保留到0.1 μm。从表2中可以看出,最小二乘法(LSM)得到的球度误差为1.189 8 μm,粒子群算法得到的结果为1.000 0 μm,本文方法得到的球度误差为1.000 0 μm。可以得出:粒子群算法和本文方法都比最小二乘法的结果更精确。从迭代次数和消耗时间来看,粒子群优化算法消耗时间大约是本文方法消耗时间的20倍,且本文方法对构造数据的处理结果与预设值完全一致,证明了本文方法不存在原理和模型误差,可以得到完全符合球度误差最小包容区域法定义的精确解,而且耗时短、效率高。
3.2 实例验证
利用文献[14,16]中的数据对本文提出的方法进行验证,利用最小二乘法(LMS)、自适应权重的粒子群(PSO)算法、本文方法,以及文献[14]中的方法对文献[14]中的384数据进行处理,结果如表3所示;同样,利用最小二乘法(LMS)、自适应权重的粒子群(PSO)算法、本文方法,以及文献[16]中的方法对文献[16]中的50数据进行处理,结果如表4所示,其中,粒子群算法的参数设置与3.1节一致。
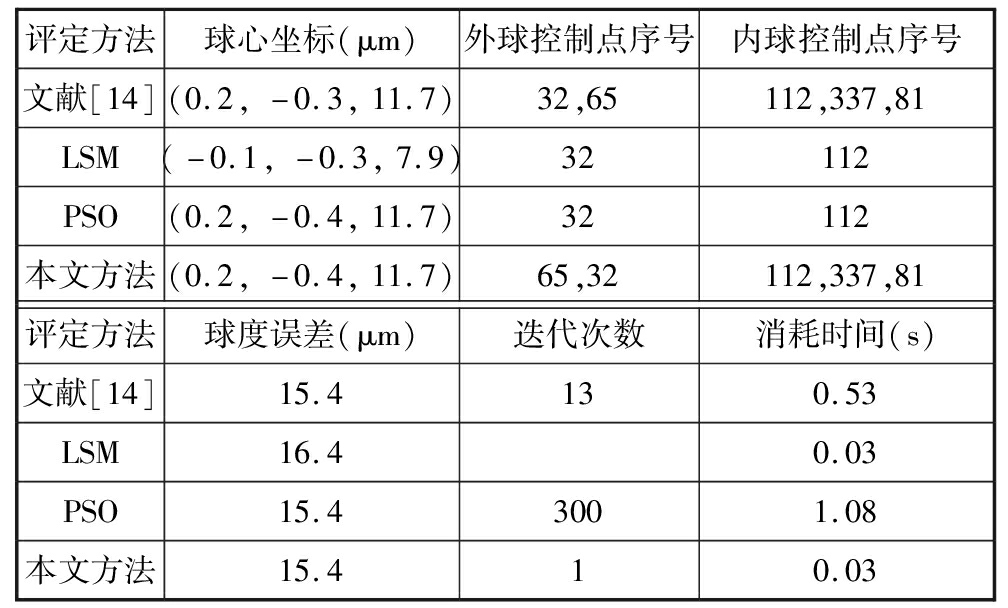
表3 文献[14]中384个数据处理结果
Tab.3 Results of 384 data in document[14]
评定方法球心坐标(μm)外球控制点序号内球控制点序号文献[14](0.2,-0.3,11.7)32,65112,337,81LSM(-0.1,-0.3,7.9)32112PSO(0.2,-0.4,11.7)32112本文方法(0.2,-0.4,11.7)65,32112,337,81评定方法球度误差(μm)迭代次数消耗时间(s)文献[14]15.4130.53LSM16.40.03PSO15.43001.08本文方法15.410.03
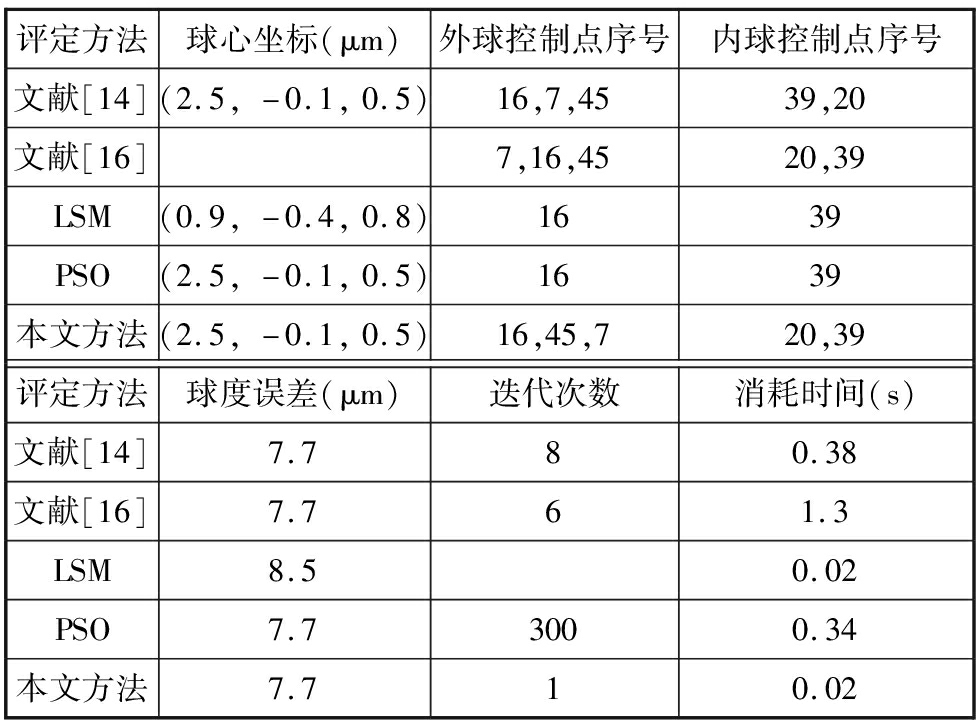
表4 文献[16]中50个数据的处理结果
Tab.4 Results of 50 data in document[16]
评定方法球心坐标(μm)外球控制点序号内球控制点序号文献[14](2.5,-0.1,0.5)16,7,4539,20文献[16]7,16,4520,39LSM(0.9,-0.4,0.8)1639PSO(2.5,-0.1,0.5)1639本文方法(2.5,-0.1,0.5)16,45,720,39评定方法球度误差(μm)迭代次数消耗时间(s)文献[14]7.780.38文献[16]7.761.3LSM8.50.02PSO7.73000.34本文方法7.710.02
考虑到实际应用,因此将表中球心坐标和球度误差结果都保留到0.1 μm。从表3、表4中可以看出,最小二乘法结果不符合最小包容区域定义,存在原理误差,所以得不到球度误差的精确解;本文方法的评定结果与文献[14,16]中提出方法评定结果以及粒子群算法的评定结果一致,说明了提出的球度误差评定方法的正确性,且本文提出方法的迭代次数更少、效率更高。本文方法对384个数据处理和50个数据处理所消耗的时间基本相同,证明了该方法的效率几乎不受采样点数据量的影响,这是因为该方法只需确定采样点中5个控制点的位置,而与其他采样点无关。
4 结论
(1)本文提出的球度误差最小包容区域评定方法结合了几何搜索逼近算法、球度误差最小包容区域法评定的几何结构和定义,原理简单,不存在原理误差,也不需满足“小偏差”假设,克服了区域搜索法、智能优化算法和线性规划理论等近似方法不能准确找到最小包容区域球心的缺点。仿真和实例证明了此方法可以准确进行球度误差的最小包容区域法评定。
(2)提出的球度误差最小包容区域评定方法符合定义,得到的球度误差为精确解;对采样点数据的分布和数据量大小没有要求,具有广泛的适用性;对控制点的判断、调整过程类似于控制系统中的“负反馈调节”,对于每一组给定数据,利用上述评定方法得到的结果非常稳定。
(3)本文方法的效率主要依赖几何搜索逼近算法的精度,而几何逼近搜索算法的精度是由搜索球的半径阈值(初始值取vLS/1000)决定的。理论上,可以通过减小阈值来提高几何逼近搜索算法的精度,但这会导致计算量的增大,使得效率降低。在实际中,依据本文设置的初始参数值,利用程序对仿真的几十乃至上千个数据进行处理的结果与预设值完全一致。采有本文方法对其他文献中的已得到最小包容区域球度误差的数据进行了评定,处理结果与文献所得结果完全一致,且实际运行时程序一般迭代一或两次,耗时短、效率高。
[1] GB/T 24632.1—2009产品几何技术规范(GPS)圆度 第1部分:词汇和参数[S].北京:中国标准出版社,2009.
GB/T 24632.1—2009 Geometrical Product Specifications(GPS)—Roundness—Part 1:Vocabulary and Parameters of Roundness[S].Beijing:Standards Press of China,2009.
[2] GB/T 24632.2—2009产品几何技术规范(GPS)圆度 第2部分:规范操作集[S].北京:中国标准出版社,2009.
GB/T 24632.2—2009 Geometrical Product Specifications(GPS)—Roundness—Part 2:Specification Operators[S].Beijing:Standards Press of China,2009.
[3] 刘盾,邓乾发,李振,等.球度测量及其评定方法现状分析[J].光学仪器,2010,32(6):86-90.
LIU Dun,DENG Qianfa,LI Zhen,et al.Analysis of Current Sphericity Measurement and Its Evaluation Methods[J].Optical Instruments,2010,32(6):86-90.
[4] 雷贤卿,宋红卫,薛玉君,等.球度误差的网格搜索算法[J].农业机械学报,2012,43(5):222-225.
LEI Xianqing, SONG Hongwei, XUE Yujun, et al.Sphericity Error Based on Mesh Search Algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(5):222-225.
[5] 雷贤卿,高作斌,马文锁,等.基于几何搜索逼近的球度误差最小区域评定[J].计量学报,2016,37(2):123-127.
LEI Xianqing,GAO Zuobin,MA Wensuo,et al.Minimum Zone Evaluating for Sphericity Error Based on Geometry Search Approaching Method[J].Acta Metrologica Sinica,2016,37(2):123-127.
[6] CUI Changcai,CHE Rensheng,YE Dong,et al.Sphericity Error Evaluation Using the Genetic Algorithm[J].Optics and Precision Engineering,2002,10(4):333-339.
[7] 胡捷,崔长彩,黄富贵.基于动态改变权重粒子群算法的球度误差评定[J].图学学报,2012,33(5):99-103.
HU Jie, CUI Changcai, HUANG Fugui.Sphericity Error Evaluation Based on a Modified Particle Swarm Optimizer Using Dynamic Inertia Weight[J].Journal of Graphics,2012,33(5):99-103.
[8] WEN Xiulan, SONG Aiguo.An Immune Evolutionary Algorithm for Sphericity Error Evaluation[J].International Journal of Machine Tools and Manufacture,2004,44(10):1077-1084.
[9] 温秀兰,宋爱国.基于免疫进化计算的球度误差评定[J].计量学报,2005,26(1):12-15.
WEN Xiulan,SONG Aiguo.Sphericity Error Evaluation Based on the Immune Evolutionary Computation[J].Acta Metrologica Sinica,2005,26(1):12-15.
[10] 王雪.基于切比雪夫逼近理论的形状误差评定算法研究[D].北京:北京工业大学,2012.
WANG Xue.Algorithm for Form Error Evaluation Based on Chebyshev Approximation Theory[D].Beijing: Beijing University of Technology,2012.
[11] 刘文文,邓善喜,聂恒敬.球度误差包容评定的高精度实现方法[J].计量学报,2000,21(2):100-105.
LIU Wenwen, DENG Shanxi, NIE Hengjing.High Precision Algorithm for Evaluation of Sphericity Error[J].Acta Metrologica Sinica,2000,21(2):100-105.
[12] SAMUEL G L, SHUNMUGAM M S.Evaluation of Sphericity Error from Coordinate Measurement Data Using Computational Geometric Techniques[J].Computer Methods in Applied Mechanics and Engineering, 2001, 190(51):6765-6781.
[13] 刘飞,徐光华,梁霖,等.最小区域球度误差评价的弦线截交方法[J].机械工程学报,2016,52(5):137-143.
LIU Fei, XU Guanghua, LIANG Lin, et al.Intersecting Chords Method in Minimum Zone Evaluation of Sphericity Deviation[J].Journal of Mechanical Engineering, 2016, 52(5):137-143.
[14] LIU Fei, XU Guanghua, LIANG Lin.Minimum Zone Evaluation of Sphericity Deviation Based on the Intersecting Chord Method in Cartesian Coordinate System[J].Precision Engineering,2016,45:216-229.
[15] CHEN Cha’o-Kuang, LIU Chien-Hong.A Study on Analyzing the Problem of the Spherical Form Error[J].Precision Engineering,2000,24:119-126.
[16] FAN Kuangchao,LEE Jichun.Analysis of Minimum Zone Sphericity Error Using Minimum Potential Energy Theory[J].Precision Engineering,1999,23:65-72.
