0 引言
针对复杂产品设计过程，国内外学者开展了多视角的创新设计方法研究。LU等[1-2]基于公理设计理论，从主观性和客观性方面讨论了复杂产品设计的本质；张鹏等[3]提出了一种基于附加效应的设计过程复杂性分析过程模型，通过分析产品设计过程中复杂性产生的原因，将其转化为附加效应链；李玉鹏等[4]运用区间数、三角模糊数、直觉模糊数和区间直觉模糊数对复杂产品指标进行合理赋值，提出一种复杂产品模块划分方法，降低了产品设计的复杂性。上述方法可有效提高复杂产品的设计研发效率，但仅停留在物理和技术层面的设计方法已不能满足人们的需求，还需要考虑设计系统的非线性、耦合性、时变性、交融性等特点，将主观的功能分析变为子系统量化分析，使产品设计过程更趋于规律化、系统化与理论化。因此面向复杂产品性能，研究产品设计参数的模糊性以及产品性能与系统非线性的关系等是十分必要的。
针对复杂产品设计过程和设计参数模糊性，本文提出了基于理想度和粗糙集理论的概念设计求解过程模型，通过理想度计算确定目标子系统，基于粗糙集理论构建产品设计特性-设计需求映射矩阵，分析并确定复杂属性，应用发明问题解决理论(theory of inventive problem solving，TRIZ)工具集消除系统复杂性，得到产品创新方案。
1 基于产品创新的设计过程基本原理
产品创新优化设计是一个概念性的综合知识与经验的信息处理过程，随着对TRIZ [5-7]的深入研究和面向系统的复杂化，针对该理论在产品概念设计阶段对设计特性和设计需求评估的模糊不确定性，将设计过程复杂性理论中的功能分析推演和系统复杂性判定与TRIZ相结合，使产品设计过程趋于规律化、系统化与理论化[8]。
设计过程复杂性理论[9-11]中，产品族概念设计复杂性是对系统各个子功能实现不确定性的度量。若系统功能实现概率不确定性较高，那么该系统各个子功能不满足独立要求，输出结果不能得到保证。在该理论中，设计结果体现的实际概率密度函数决定系统的范围，在给定满足功能需求的设计参数后，用设计范围和系统范围相交的公共范围表征系统的复杂性。公共范围越大，系统复杂性越低，如图1所示。
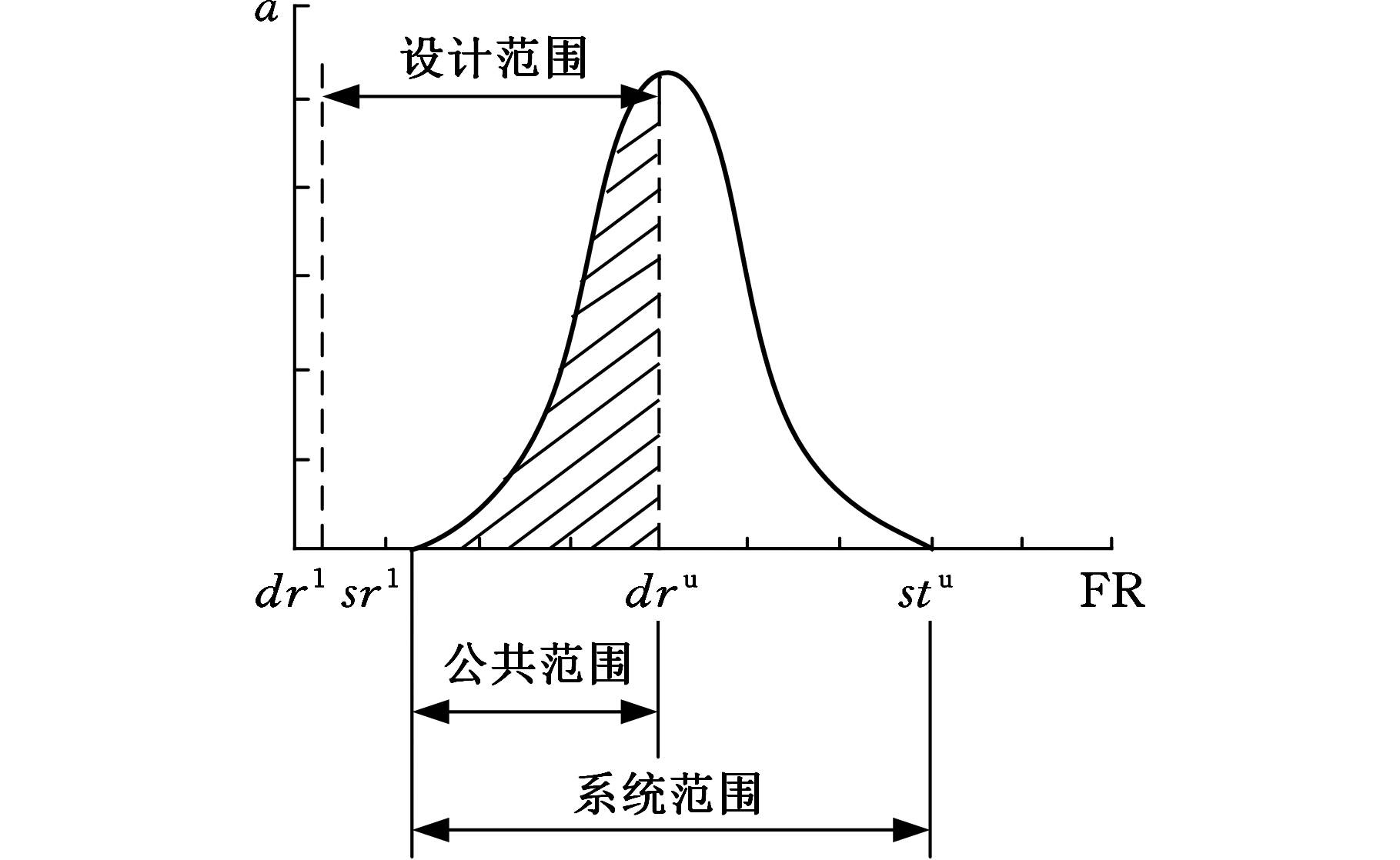
图1 系统概率密度函数
Fig.1 System probability density function
图1中，FR表示功能需求；a为系统功能实现概率密度；dr1、dru分别为设计范围的下限和上限；sr1、sru分别为系统范围的下限和上限。概率密度函数与公共范围所围成的面积Acr表征信息含量I，即设计目标实现特定需求的可能，其公式为
I=-lnAcr
(1)
TRIZ能最大限度地发挥人类才智，合理高效地填充系统设计缝隙，但在设计初期却没有给出操作性强的设计冲突的分析推演方法。将TRIZ和设计过程复杂性理论有机结合，根据复杂性及复杂性与信息含量之间的关系对系统进行推演与判定，再将理想度和粗糙多属性决策纳入复杂性理论的映射机理，就能建立基于TRIZ的客观数学模型，从而实现对设计过程的定量化处理，减小了传统概念设计的主观性，更好体现复杂机电系统的非线性、动态演化性和开放性等特征，提高研发质量，缩短设计研发周期。
2 基于理想度和粗糙集理论的设计过程复杂性创新模型
2.1 基于理想度的设计过程复杂性模糊前端判定
针对复杂产品概念设计需求，将系统分为技术系统和超系统。为体现系统的自组织性，使系统描述更加规范化，根据集合理论将系统定义为系统集合、目标技术系统集合与超系统集合。将具有系统特征的部件和部件相互关系的技术系统归于目标技术系统集合。技术系统由多个子系统组成，并通过子系统间的相互作用实现产品功能。在目标技术系统集合以外，与目标技术系统相互作用的超系统构成超系统集合，系统集合、目标技术系统集合与超系统集合之间的关系如图2所示。在产品概念设计问题分析前期应将目标技术系统集合与超系统集合进行明确区分，并分析两者之间的相互作用，体现系统的开放性，为系统分析奠定基础。
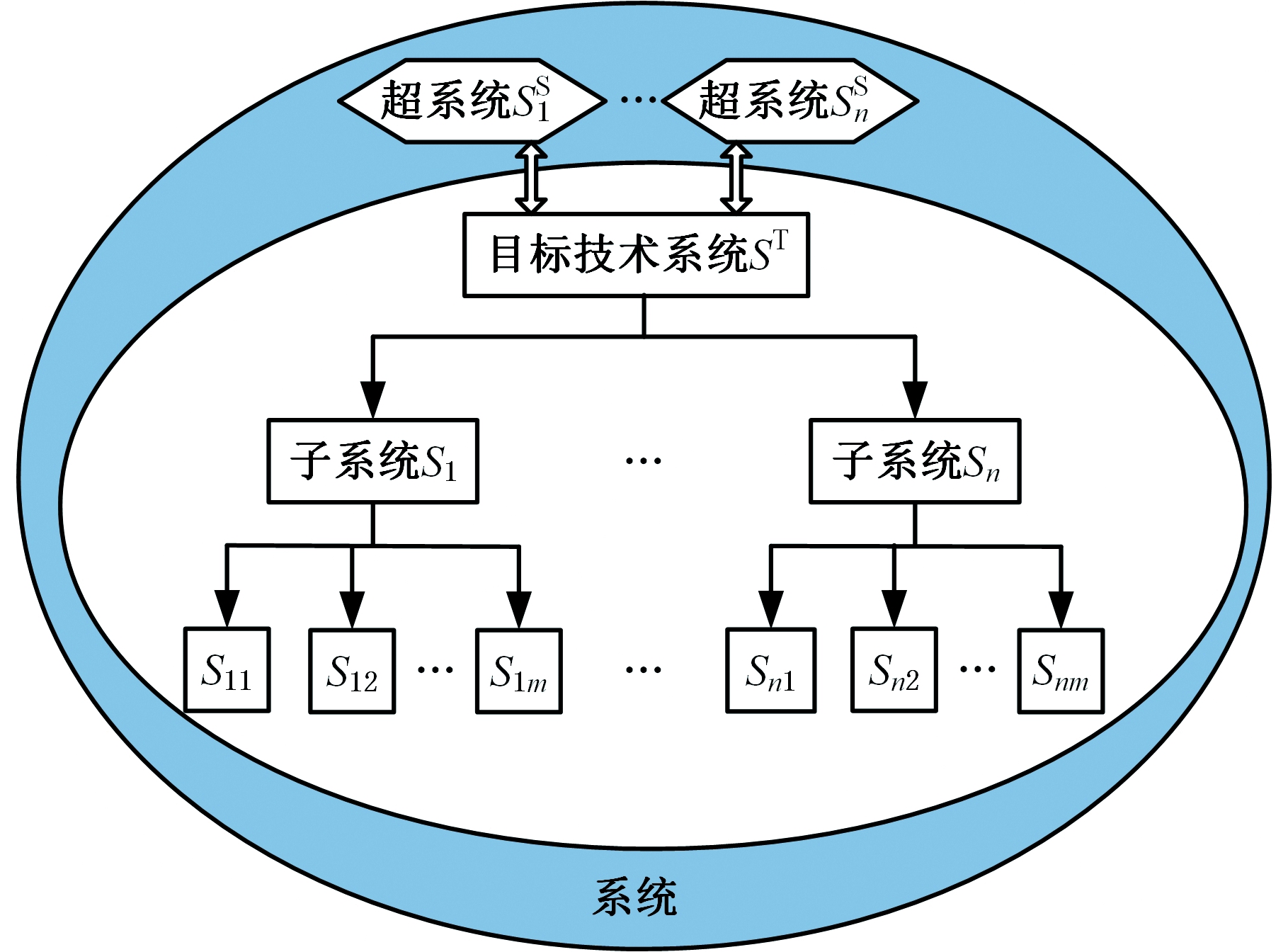
图2 系统集合关系
Fig.2 System set relation
系统集合S、目标技术系统集合ST、超系统集合SS之间的关系可描述为
S=ST∪SS
(2)
TRIZ中，理想化是不考虑现有约束因素的影响而所达到的最优状态，包括理想方法、理想资源、理想系统及理想物质等。在技术系统领域，同一功能存在多种技术实现，任何系统在满足用户需求时，都有附加作用。采用理想度对系统的正反两方面作用进行定量评价：
(3)
式中，
表示一级子系统理想化水平，i=1，2，…，n；n为一级子系统的个数；m为一级子系统组元的个数；Bj为满足组元功能需求的效益参数；Ej为影响功能需求实现的组元代价参数；Hj为影响功能需求实现的组元危害参数。
式(3)中的代价包括原料成本、系统占用的空间、消耗的能量及产生的噪声等，危害包括废弃物及污染等。产品创新的目标是不断提高产品理想化水平，通过增加有用功能、提高有用功能级别、降低成本、减少有害功能、降低有害功能级别和移除有害功能等六个方面的措施，确定系统问题的位置，明确系统的改进方向，为进一步消除系统问题、提升系统理想化水平做好准备。
将理想度与设计过程复杂性理论中的信息含量进行融合，因此基于理想度的第i个子系统的信息含量可表示为
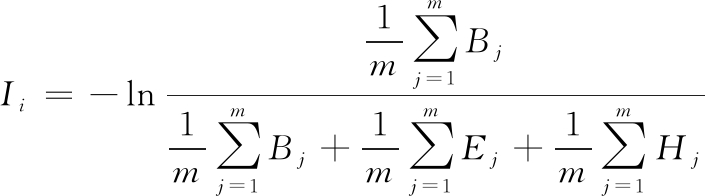
(4)
由此，系统总的信息含量为
(5)
定义
时，系统效益影响因素与系统非效益影响因素的比值趋于无穷，可以满足系统功能需求，系统信息含量趋于零，不存在设计过程复杂性。r=C时，系统效益影响因素与系统非效益影响因素的比值趋于常数，系统的信息含量I范围是(0, 1)，系统功能需求部分被满足，并存在复杂性，需要减小系统中非效益影响因素的干扰，不需调整整体系统结构。r→0时，系统效益影响因素与系统非效益影响因素的比值趋于0，系统信息含量趋于无穷，系统功能需求无法被满足，且存在复杂性，这时需要调整系统结构。
2.2 基于粗糙集理论的设计过程复杂性判定
为有效分析和处理系统在概念设计过程中遇到的不确定性和不完全性问题，采用粗糙集理论研究不同类对象组成的集合之间的关系，将主观存在的隐含知识进行约简化处理，导出问题的决策方向。在粗糙集理论[12-14]中，一个划分δ={x1, x2, …, xn}，令i, j=1, 2, …,n，则有
且i≠j时，xi∩xj=∅。
论域U上任何概念族的划分称为关于U的一个知识库(关系系统)。设R是U上的一组等价关系，U/R表示所有等价类构成的集合，[x]R表示包含元素x∈U的R的等价类，则知识库可以表示为K=(U, R)。将上述概念引入产品创新设计领域，在论域U中，令R为目标技术系统设计特性，xi表示目标技术系统设计子特性。在粗糙集理论中，划分集pi可以用粗糙数RXi表示，RXi的粗糙上限和粗糙下限定义为
具有上下限的粗糙数能够更好地反映设计特性及需求的不确定性，同时保持原始设计信息的客观性。决策主体采用1～9标度法给出的评估值表征各设计特性之间的相对重要性，标度值越大，产品设计特性影响程度越高。产品设计需求权重为
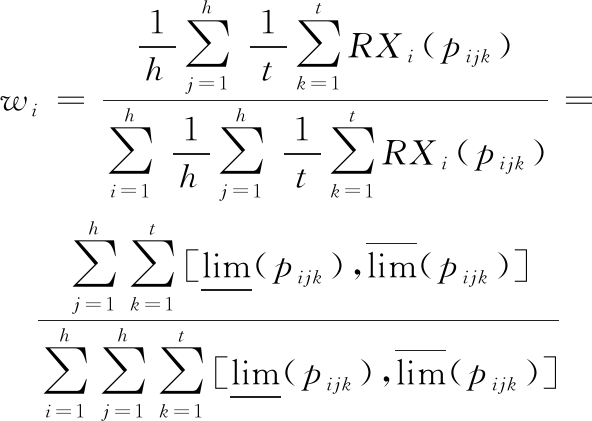
(6)
式中，pijk为由第k个决策主体给出的第i个设计特性相对于第j个设计特性的评估值；h为设计特性个数；t为决策主体个数；RXi(pijk)为第i个设计特性相对于第j个设计特性的粗糙数值；
分别为粗糙集边界的上下界，粗糙集是由具有上下边界数组成的集合。
构建产品设计特性-设计需求关联矩阵，矩阵元素采用具有上下界的粗糙数表示，基于1～9标度法的评估值表示各设计需求或设计特性之间的关联程度，标度值越大，设计特性与设计需求关联程度越大。产品设计需求绝对评价结果为
(7)
式中，r′ij为第i个设计特性相对于第j个设计需求的评估值;RXi(r′ij)为第i个设计特性相对于第j个设计需求的粗糙数值。
将产品设计需求绝对评价结果进行归一化处理，得到产品设计需求相对评价结果：
(8)
式中，g为设计需求个数。
明确设计目标后，需要基于公理设计理论对设计目标进行复杂性集合评判，将复杂性分为时间依赖复杂性和时间独立复杂性。当系统复杂性随时间变化时，属于时间依赖复杂性，可以分为组合复杂性和周期复杂性。时间独立复杂性与时间无关，包括真实复杂性和虚拟复杂性互相正交的两部分。
在设计过程复杂性理论的概率密度函数图中，当系统范围与公共范围不重合时，真实复杂性CR表示系统各个子功能实现概率小于1不确定性的度量，该不确定性由非阴影面积确定。虚构复杂性CI具有不确定性，是由设计者对系统本身认知存在欠缺而导致的。在组合复杂性CC中，复杂性组合的数量会随时间的延长而持续增大，并导致系统复杂性增高。周期复杂性CP是在时间依赖的基础上，在给定周期内可能存在由组合或其他复杂性产生的不确定性。组合复杂性可以转换为周期复杂性，从而降低系统复杂性。复杂性集合关系可表示为
C=CR∪CI∪CC∪CP
(9)
2.3 设计过程复杂性创新模型
基于理想度和粗糙集理论的产品设计过程复杂性概念求解模型如图3所示，具体步骤如下：
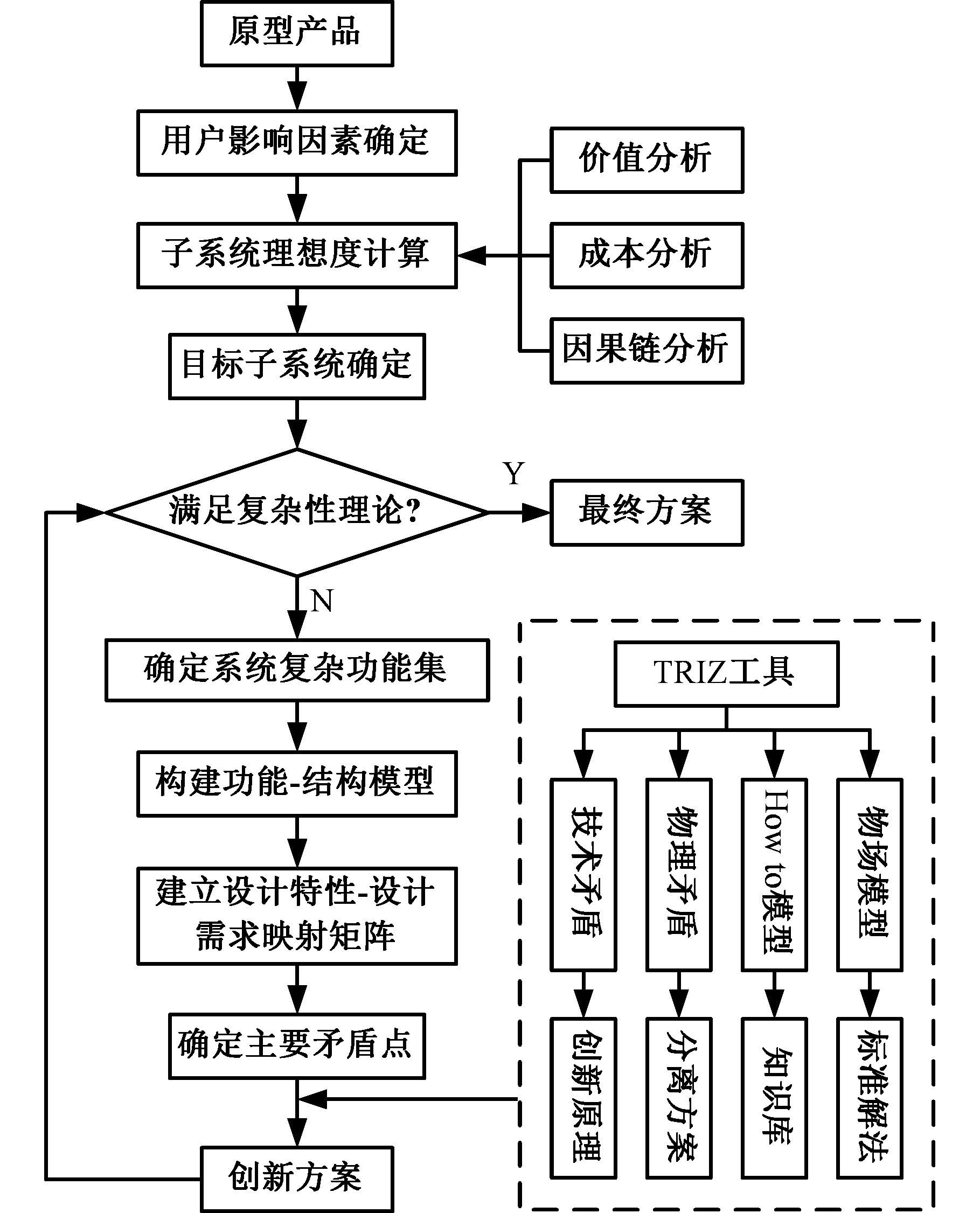
图3 概念设计创新模型
Fig.3 Conceptual design innovation model
(1)确定目标技术系统集合与超系统集合，分析两集合中各元素的相互作用关系，明确用户需求影响因素。
(2)基于式(3)对目标技术系统集合中的各个子系统进行理想度求解，确定目标子系统，根据理想度值和复杂性理论确定问题属性。
(3)明确系统主要目标对象，识别直接作用和间接作用在该对象上的功能及关联组元，明确各个组元间的相互作用关系，建立目标技术系统与超系统的功能结构模型，将超系统纳入功能结构模型，了解系统构成，为后期系统分析做准备。
(4)基于系统功能需求，初步进行产品设计特性分解，建立产品设计特性层次结构图，采用粗糙数构建产品设计特性重要度矩阵，求解产品设计特性权重集。
(5)根据产品功能结构图对目标子系统分解，得到设计需求集合，构建产品设计特性-设计需求映射矩阵，求解设计需求相对评价结果，确定主要目标，缩小矛盾点范围，明确复杂性属性。
(6)利用复杂性理论对主要目标进行分析，明确导致设计过程复杂性的技术参数，然后将其转化为TRIZ标准工程参数，应用TRIZ消解工具求解系统原理解，最终得到产品创新方案。
(7)利用复杂性理论分析创新系统是否存在复杂性，若依然存在复杂性，则返回步骤(2)。
3 下肢外骨骼创新优化案例分析
下肢外骨骼机器人[15-16]是一种可并联穿戴于人体，为人体提供助力的腿型机械系统。该系统理想设计目标是机构拟人化。下肢外骨骼机器人工作时直接与人体捆绑，其性能直接影响穿戴者的使用效果，为了加强下肢外骨骼机器人设计的合理性，采用基于理想度与粗糙数多属性决策的复杂非线性系统设计方法对下肢外骨骼系统进行分析，求解该系统创新优化方案。
3.1 基于理想度的模糊判定模型
在下肢外骨骼系统设计初期，应先识别目标技术系统集合与超系统集合，并分析目标技术系统与超系统间的相互作用关系，目标技术系统集合ST={下肢外骨骼系统}={驱动系统，机械结构系统，传感系统，控制系统}，超系统集合SS={人，车，路面}。基于式(2)，该案例中的目标技术系统集合ST与超系统集合SS可得系统集合S={驱动系统，机械结构系统，传感系统，控制系统}∪{人，车，路面}。
首先，因为下肢外骨骼机器人小腿杆、大腿杆和髋关节利用绑带与人体固定，所以设备运动方式决定人体下肢运动方式。下肢外骨骼机器人通过足底与路面产生接触，将机械能转化为摩擦能耗，促使人迈步前进。下肢外骨骼足底与路面接触时会对用户产生不确定性的附加作用，这种不确定性主要取决于路面状况，而原始的下肢外骨骼并未对这种不确定性附加作用进行有效补偿，导致原始下肢外骨骼无法满足用户行走时的稳定性要求。此外，超系统指向下肢外骨骼机器人的附加作用还包括下肢外骨骼快速反应能力欠佳时，人、车等事物对其平衡性的影响。
对驱动系统、机械结构系统、传感系统和控制系统采用专家评价法对效益、代价和危害进行数值评价，并将评价数值代入式(3)进行下肢外骨骼子系统理想度计算，计算结果见表1。同时将子系统效益、代价和危害数值导入式(4)，计算基于理想度的每个子系统的信息含量，并根据式(5)对下肢外骨骼子系统信息含量进行求和，得出该系统总的信息含量0<I<1，因此系统功能需求部分被满足，存在复杂性，需要对下肢外骨骼系统进行优化。由表1可得，机械结构系统
理想度为1.25，该子系统理想度最低，因此对下肢外骨骼系统复杂性影响最大，由此判定该系统目标子系统为
明确下肢外骨骼系统目标子系统为
识别直接作用或间接作用在该对象主要元件上的功能或关联组元，了解系统构成，建立系统和超系统功能结构模型，如图4所示。
表1 下肢外骨骼子系统理想度数值表
Tab.1 Lower extremity exoskeleton subsystem ideal degree numerical table
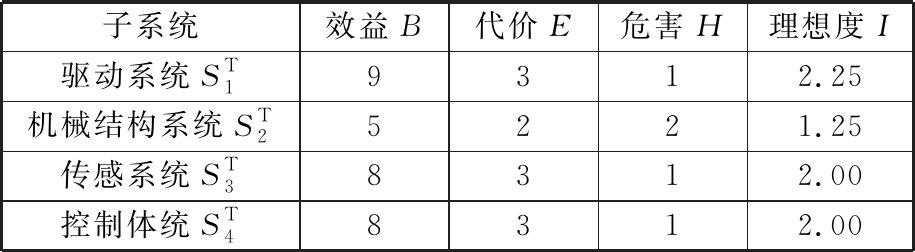
子系统效益B代价E危害H理想度I驱动系统ST19312.25机械结构系统ST25221.25传感系统ST38312.00控制体统ST48312.00
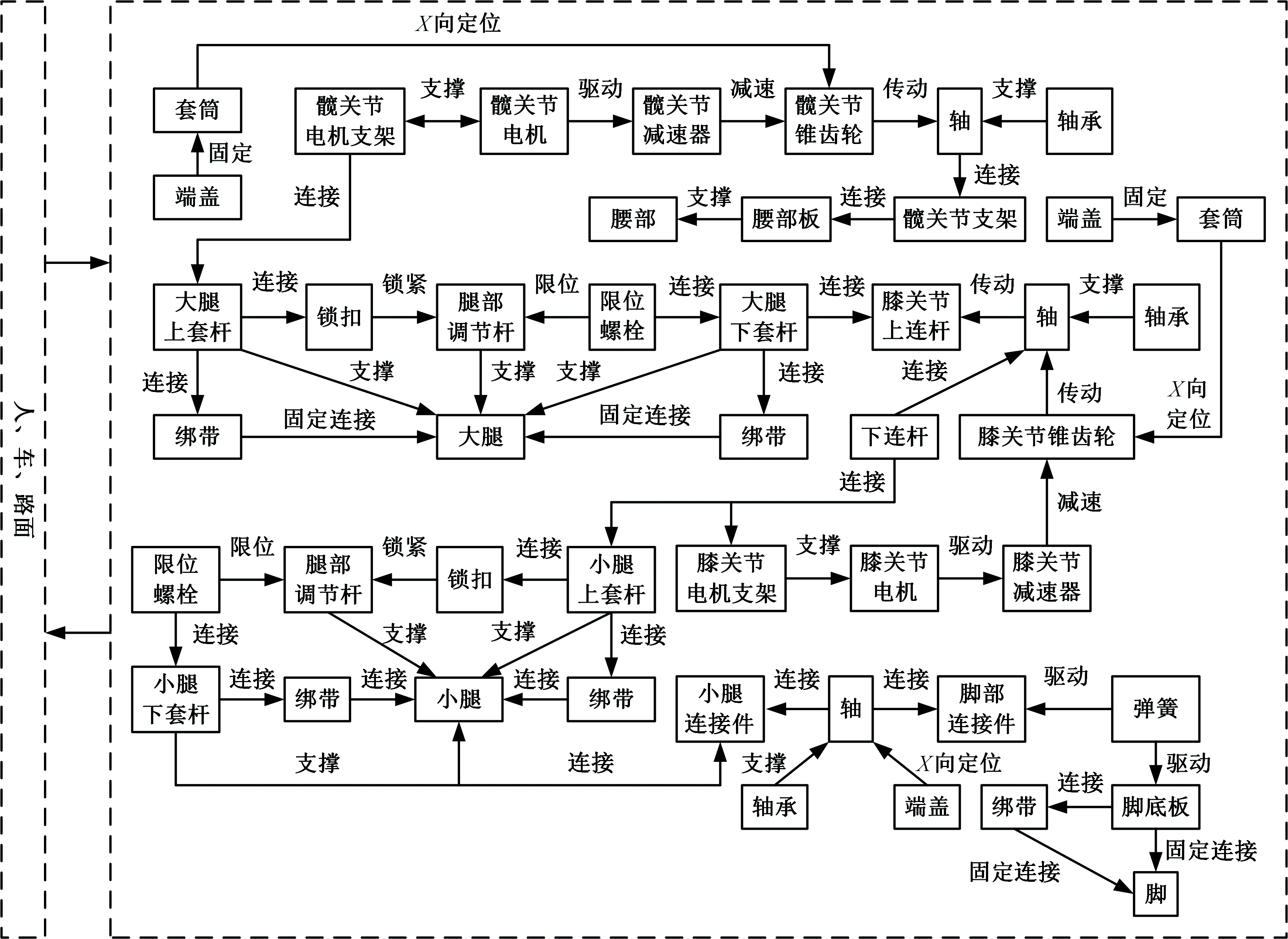
图4 下肢外骨骼系统功能结构模型
Fig.5 Functional structure model of lower extremity exoskeleton system
3.2 基于粗糙多属性驱动的映射矩阵模型
根据下肢外骨骼机器人系统功能需求，初步进行产品设计特性分解，构建产品设计特性层次结构图(图5)。
根据粗糙集理论可定义3个等价属性：工作可靠性R1、经济性R2、使用性能R3，通过这些等价关系，可以得到下面3个等价类：
U/R1={d1, d2, d3}
U/R2={d4, d5, d6}
U/R3={d7, d8, d9}
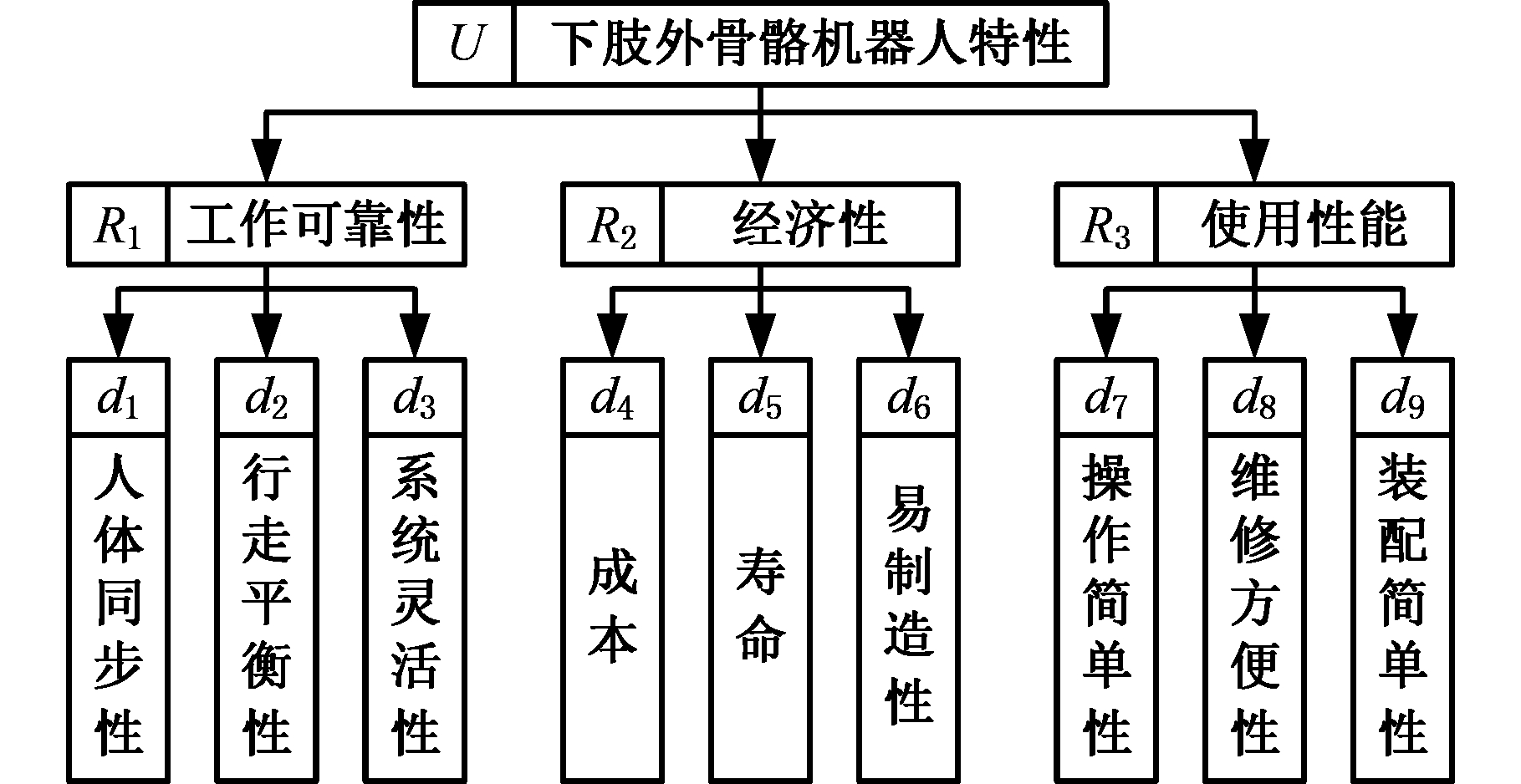
图5 下肢外骨骼机器人性能结构图
Fig.5 Performance structure diagram of lower extremity exoskeleton robot
针对下肢外骨骼机器人功能需求，对每个集合元素产品设计特性进行两两比对，采用1～9标度法对对比结果进行量化。基于粗糙数构建下肢外骨骼机器人设计特性重要度矩阵参数，见表2。将表2中由决策主体给出的设计特性相对评估值的上下限分别代入式(6)，对粗糙数上下限进行求和均值处理后，进行数值归一化计算，得出各设计特性重要度集W={0.15, 0.17, 0.15, 0.12, 0.09, 0.09, 0.10, 0.07, 0.06}。
根据下肢外骨骼功能结构图对目标子系统
进行分解，最终得到
其中，设计需求DR1为髋关节结构，DR2为膝关节结构，DR3为踝关节结构，DR4为腿部连接杆，DR5为足部结构。构建下肢外骨骼机器人设计特性-设计需求映射矩阵，将表2中各个设计特性相对于各个设计需求的粗糙数与权重值别代入式(7)，对粗糙数与权重的积进行求和处理，得出设计需求绝对评价结果，最后将设计需求绝对评价结果代入式(8)，经归一化处理后，得到设计需求相对评价结果，见表3。
表2 下肢外骨骼机器人设计特性重要度矩阵参数
Tab.2 Parameters of importance matrix of design characteristics of lower extremity exoskeleton robot
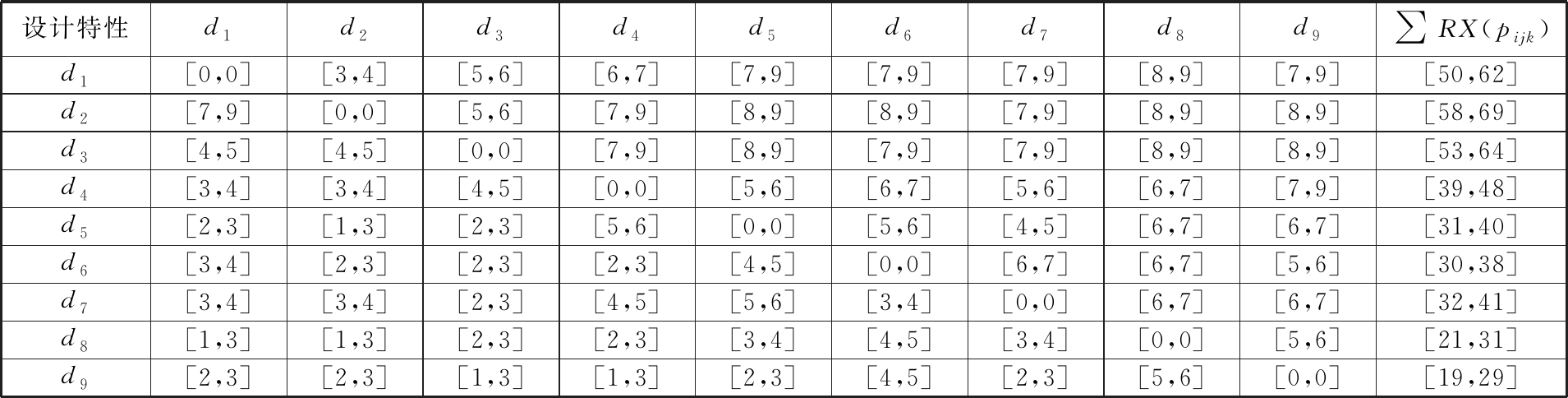
设计特性d1d2d3d4d5d6d7d8d9∑RX(pijk)d1[0,0][3,4][5,6][6,7][7,9][7,9][7,9][8,9][7,9][50,62]d2[7,9][0,0][5,6][7,9][8,9][8,9][7,9][8,9][8,9][58,69]d3[4,5][4,5][0,0][7,9][8,9][7,9][7,9][8,9][8,9][53,64]d4[3,4][3,4][4,5][0,0][5,6][6,7][5,6][6,7][7,9][39,48]d5[2,3][1,3][2,3][5,6][0,0][5,6][4,5][6,7][6,7][31,40]d6[3,4][2,3][2,3][2,3][4,5][0,0][6,7][6,7][5,6][30,38]d7[3,4][3,4][2,3][4,5][5,6][3,4][0,0][6,7][6,7][32,41]d8[1,3][1,3][2,3][2,3][3,4][4,5][3,4][0,0][5,6][21,31]d9[2,3][2,3][1,3][1,3][2,3][4,5][2,3][5,6][0,0][19,29]
表3 下肢外骨骼机器人设计特性-设计需求映射矩阵
Tab.3 Lower extremity exoskeleton robot design characteristics-design requirements mapping matrix
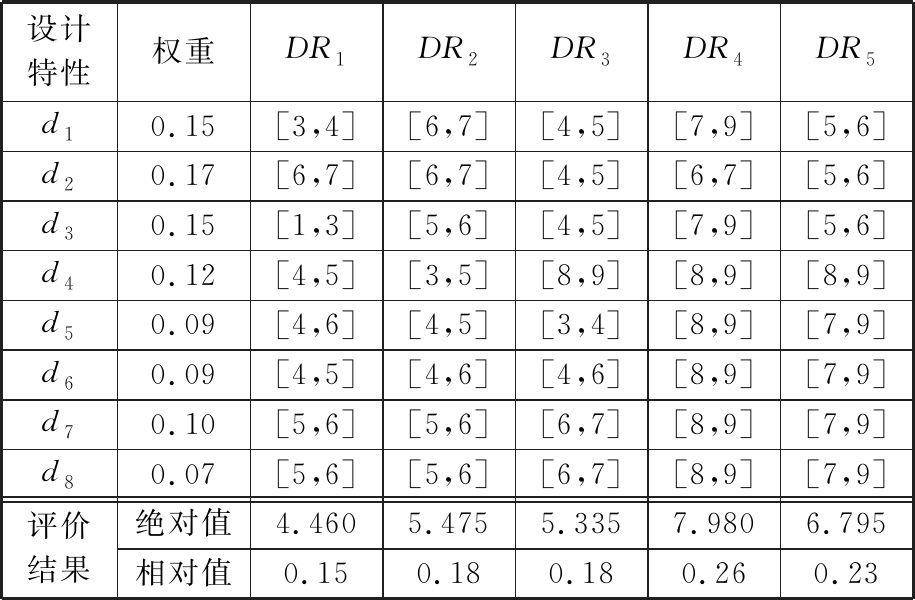
设计特性权重DR1DR2DR3DR4DR5d10.15[3,4][6,7][4,5][7,9][5,6]d20.17[6,7][6,7][4,5][6,7][5,6]d30.15[1,3][5,6][4,5][7,9][5,6]d40.12[4,5][3,5][8,9][8,9][8,9]d50.09[4,6][4,5][3,4][8,9][7,9]d60.09[4,5][4,6][4,6][8,9][7,9]d70.10[5,6][5,6][6,7][8,9][7,9]d80.07[5,6][5,6][6,7][8,9][7,9]评价结果绝对值4.4605.4755.3357.9806.795相对值0.150.180.180.260.23
3.3 下肢外骨骼系统复杂性判定与创新方案
由表3可知，DR1的设计需求相对评价结果数值较小，所以DR1对系统复杂性影响较大，DR1为髋关节结构，所以利用TRIZ对髋关节进行分析，确定导致系统出现设计过程复杂性的关键技术参数。初始结构中，髋关节利用电机驱动锥齿轮，实现髋关节的屈伸运动，自由度为1，灵活性较差，环境适应性也较差。通过分析系统所含的设计过程复杂性，即哪些参数会导致下肢外骨骼髋关节理想效益过低，可知影响系统理想效益过低的主要原因有两个，分别是穿戴者髋关节灵活性较低导致系统稳定性差以及下肢外骨骼机器人环境适应性低。由复杂性理论定义可知，髋关节灵活性和适应性较差的问题属于时间独立真实复杂性，需要运用TRIZ消解工具对复杂性进行消除，参照TRIZ标准工程参数可知，该冲突改善参数为可靠性、适用性及多用性，恶化参数为静止物体的重量、装置复杂性。
根据改善参数和恶化参数查阅TRIZ矛盾矩阵表(矛盾矩阵局部见表4)得到推荐发明原理。表4中，13为逆向思维原理；35为参数变化原理；1为分割原理；3为局部质量原理；10为预操作原理；8为重量补偿原理；28为机械系统的替代原理；15为动态化原理；29为气动与液压结构原理；37为热膨胀原理；19为周期性动作原理；16为局部作用或过量作用原理。
表4 TRIZ矛盾矩阵局部表
Tab.4 Local table of TRIZ contradiction matrix
改善参数恶化参数36装置的复杂性2静止重量27可靠性13,35,13,10,8,2835适用性及多用性15,29,37,2819,15,29,16
根据下肢外骨骼机器人设计需求，分析技术冲突TC1中的发明原理，运用发明原理35(参数变化)中的第二条：“改变系统或对象的任意属性来实现系统的新功能”，考虑将下肢外骨骼结构材料换为强度大、重量轻的材型。
分析技术冲突TC2中的发明原理，运用发明原理28(机械系统的替代)中的第三条：“将固定场变为移动场，将静态场变为动态场，将随机场变为确定场”，将下肢外骨骼机器人由原来四自由度机构变为五自由度机构。下肢外骨骼机器人既有向前迈步的功能，还具有改变前进方向的功能，因此除了实现髋关节与膝关节的屈伸以及踝关节的跖屈/背屈、内翻/外翻外，还需增加髋关节的外展/内收功能。髋关节设计中，矢状面的屈伸在人体运动过程中起主要作用，因此采用电机驱动锥齿轮实现髋关节屈伸，为提升穿戴者的舒适性，需保证外骨骼屈伸自由度的中心轴与人体髋关节屈伸自由度的中心轴同轴。髋关节的外展/内收在人体运动中起辅助作用，因此采用被动驱动，通过转轴与锥齿轮串联连接，赋予了髋关节外展/内收的能力，在增加人体灵活性和可靠性的同时，减少了装置复杂性和重量，降低了系统的复杂性。髋关节创新设计如图6所示。
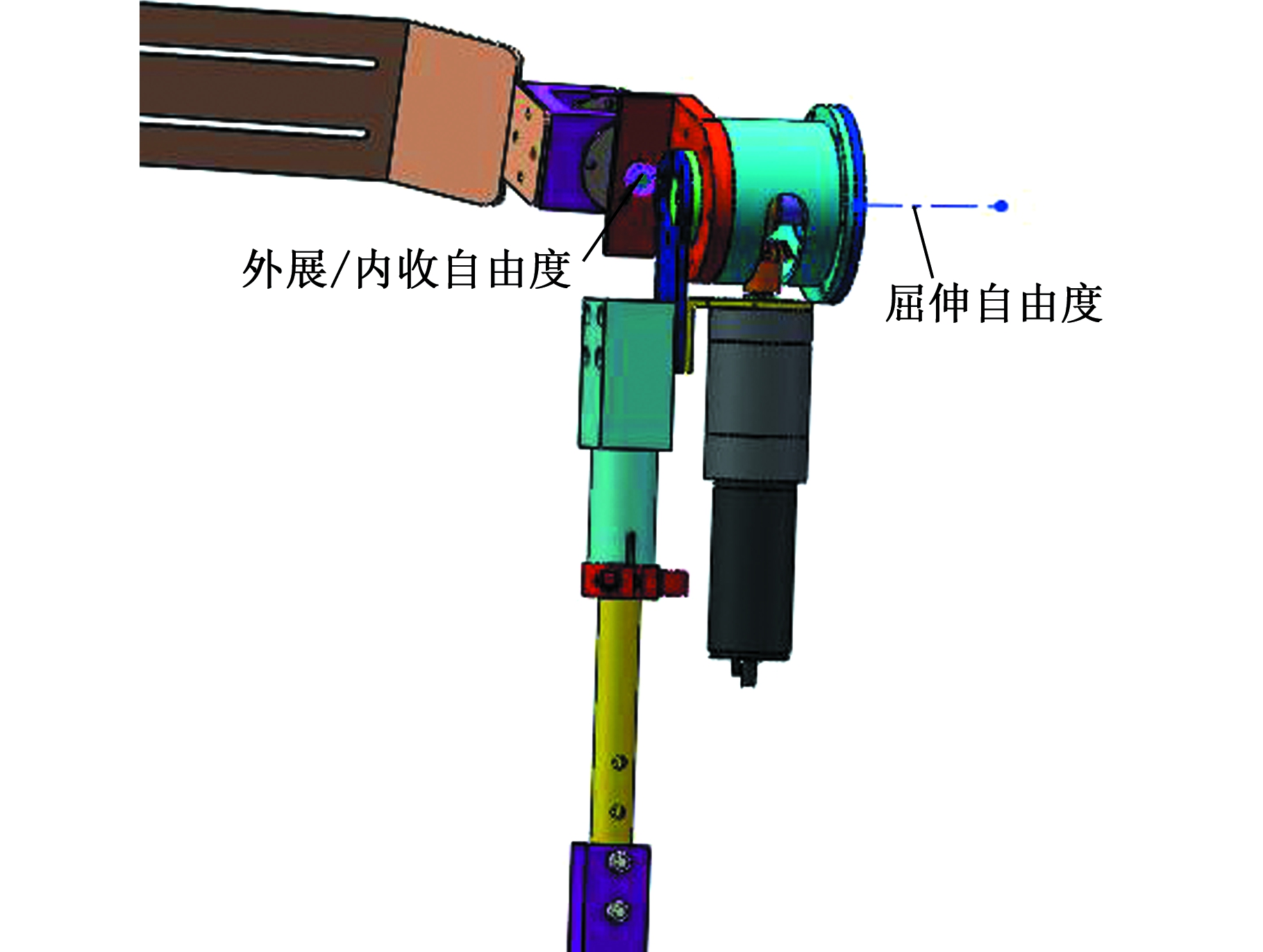
图6 下肢外骨骼机器人髋关节结构
Fig.6 Hip joint structure of lower extremity exoskeleton robot
4 结论
(1)将TRIZ、粗糙集理论和基于公理设计的复杂性理论有效结合，建立了基于三者的产品设计过程复杂性创新概念模型，为产品创新提供了定量化粗糙评价矩阵，形成了面向理想度和系统性能的概念设计方法。
(2)传统的创新设计方法无法体现目标系统的耦合性、非线性和时变性等特征。基于理想度和粗糙集理论的产品设计过程复杂性概念求解模型，提高了研发质量，减小了传统概念设计的主观性。将理想度与粗糙多属性驱动的复杂非线性系统设计分析方法应用于下肢外骨骼，得到了下肢外骨骼机器人髋关节结构创新模型，为下肢外骨骼机器人创新设计提供了新的分析与评价方法，减少了产品开发资源，降低了设计过程的复杂性。
[1] LU S C Y, SUH N P. Complexity in Design of Technology System[J]. CIRP Annals—Manufacturing Technology, 2009, 58(1):157-160.
[2] LU S C Y, LIU A. Subjectivity and Objectivity in Design Decisions[J]. CIRP Annals—Manufacturing Technology, 2011, 60(1):161-164.
[3] 张鹏,张建辉,董娅凡,等. 基于附加效应的设计过程复杂性分析过程模型[J].计算机集成制造系统, 2018, 24(2): 444-454.
ZHANG Peng, ZHANG Jianhui, DONG Yafan, et al. Analysis Process Model of Design-centric Complexity Based on Additional Effect[J]. Computer Integrated Manufacturing Systems,2018,24(2): 444-454.
[4] 李玉鹏,连晓振,卢成,等. 基于混合模糊多属性决策的复杂产品模块划分方案评价[J].上海交通大学学报, 2017, 51(11):1374-1382.
LI Yupeng, LIAN Xiaozhen, LU Cheng, et al. Evaluation Approach to Rank Module Partition Schemes of Complex Products Based on Hybrid Fuzzy Multi-attribute Decision Making[J]. Journal of Shanghai Jiao Tong University, 2017, 51(11):1374-1382.
[5] CZINKI A, HENTSCHEL C. Solving Complex Problems and TRIZ[J]. Procedia CIRP, 2016,39:27-32.
[6] 
M, KOH
R R, 
S, et al. Use the Method of TRIZ in Optimizing Automated Machine for Ultrasonic Welding[J]. Procedia Engineering, 2017, 192: 80-85.
[7] 平恩顺, 檀润华, 孙建广. 基于TRIZ的机械产品突破性创新设想产生过程研究[J]. 中国机械工程, 2014, 25(18): 2439-2446.
PING Enshun, TAN Runhua, SUN Jianguang. Research on Ideas Generation Process for Mechanical Product Radical Innovation Based on TRIZ[J]. China MechanicalEngineering, 2014, 25(18):2439-2446.
[8] ZHOU Jianqiang, GUI Fangzhi, ZHAO Yanwei, et al. Model and Application of Product Conflict Problem with Integrated TRIZ and Extenics for Low-carbon Design[J]. Procedia Computer Science, 2017, 122: 384-391.
[9] LIU Boyuan, HUANG Shuangxi, FAN Wenhui, et al. Data Driven Uncertainty Evaluation for Complex Engineered System Design[J]. Chinese Journal of Mechanical Engineering, 2016, 29(5):889-900.
[10] TAHA Z, SOEWARDI H, DAWAL S Z M. Axiomatic Design Principles in Analysing the Ergonomics Design Parameter of a Virtual Environment[J]. International Journal of Industrial Ergonomics,2014,44(3):368-373.
[11] 张鹏,董娅凡,张换高,等.设计过程复杂性理论与TRIZ理论集成复杂机电系统功能分解过程模型[J]. 机械工程学报, 2016, 52(23):17-24.
ZHANG Peng, DONG Yafan, ZHANG Huangao, et al. Functional Decomposition Process Model for Complex Electromechanical Based on Design-centric Complexity and TRIZ[J]. Journal of Mechanical Engineering, 2016, 52(23): 17-24.
[12] 鲍宏,胡迪,张城,等.基于进化潜力分析的产品低碳创新设计[J]. 计算机集成制造系统, 2018, 24(8): 2053-2060.
BAO Hong, HU Di, ZHANG Cheng, et al. Innovative Design Method for Low-carbon Product Based on Evolution Potential Analysis[J]. Computer Integrated Manufacturing Systems, 2018, 24(8):2053-2060.
[13] 于洪,王国胤,姚一豫.决策粗糙集理论研究现状与展望[J]. 计算机学报,2015(8):1628-1639.
YU Hong, WANG Guoyin, YAO Yiyu. Current Research and Future Perspectives on Decision-theoretic Rough Sets[J]. Chinese Journal of Computers, 2015(8): 1628-1639.
[14] JIA X, SHANG L, ZHOU B, et al. Generalized Attribute Reduct in Rough Set Rheory[J]. Knowledge-Based Systems, 2016, 91(C):204-218.
[15] ÜMIT N, BOTSALI F M,KALYONCU M, et al. Design and Actuator Selection of a Lower Extremity Exoskeleton[J]. ASME Transactions on Mechatronics, 2014, 19(2):623-632.
[16] BOGUE R. Robotic Exoskeletons: a Review of Recent Progress[J]. Industrial Robot, 2015,42(1):5-10.
