0 引言
随着科技的不断发展与进步,大型化、复杂化、集成化的系统和装备得到广泛应用,人们在享受高科技带来便利的同时,也面临着严峻的系统安全问题。制定合理的维护计划是提高系统可靠性及降低相应运作成本的有效途径。根据不同的系统要求,已经出现诸多系统维护建模方法[1-6]。针对复杂系统中可靠性要求较高的关键设备,将其做成冷备子系统,不仅可以提高全系统的可靠性,并且还可以很大程度上缓解突发事件对系统安全产生的不良影响。
鉴于冷备系统在实际工程领域中的实用性,近年来,冷备系统的维护策略研究已经受到工业界和学术界的广泛关注。COIT[7]对带冗余单元的混联系统进行了结构优化设计,每个子系统由多个相同的不可修部件组成,部件的寿命遵循艾朗分布,部件失效后,系统通过选择开关的跳转启动备用部件。ZHANG等[8]用几何过程描述冷备系统的工作时间,基于部件役龄和失效次数建立长期平均单位时间损失函数,以此求得最佳更换策略。WU等[9]建立了由两个部件和一个维修人员组成的冷备系统维护模型,假设部件遭受泊松冲击,部件失效后的维修时间服从一般分布。ZHONG等[10]建立了基于半马尔可夫理论和再生点技术的冷备系统预防性维护模型。JIA等[11]考虑了维修等待时间,在模型中以概率P进行及时维修或者概率1-P等待维修。LEUNG等[12]研究的冷备系统由两个不同的部件组成,部件的寿命及维修时间遵循指数分布,并且其中一个部件具有维修优先权。ZHANG等[13]基于几何过程建立了可修两部件冷备系统的维护模型,模型中假设部件的连续工作时间形成一个递减几何过程,而连续修复时间构成一个递增几何过程,考虑部件的优先使用权及修复权,当优先部件的修复次数达到一定数值时对整个系统进行更新。
上述关于冷备系统的维护模型大都只考虑单一的失效形式,然而,现实生产中,系统外部冲击和内部退化导致的失效存在本质区别,这使得对应的维修方式也存在较大差异,此外,根据不同的系统要求,对系统性能进行衡量的可靠性指标有所不同。为此,本文在维护建模中考虑了随机失效与退化失效两种失效形式,采用了小修、大修及预防性维护相结合的维护手段,并基于半马尔可夫理论和再生点技术分析了系统的状态及状态转移规律,建立了系统的首次平均失效时间和稳态可用度两个可靠性指标,并分别以系统的平均首次失效时间和稳态可用度为目标函数求解得到了最佳预防性维护策略。
1 问题描述及假设
本文所研究的冷备系统由两个相同的可修复部件组成,系统结构如图1所示。该冷备系统由部件C1和C2组成,两部件具有相同退化特征,C1表示在线部件,C2表示冷备部件,其中C1遭受随机失效过程和退化失效过程。随机失效的累积分布函数(cumulative distribution function,CDF)为F1(t),失效后进行小修,小修时间的CDF为G1(t),退化失效的CDF为F2(t),失效后进行大修,大修时间的CDF为G2(t)。 当C2可用时,在时刻点KT(K=1,2,…,n;T为预防性维护周期)对在线部件进行预防性维护。反之,则将预防性维护推迟到下一个维护时刻点。预防性维护时间的CDF为G3(t)。
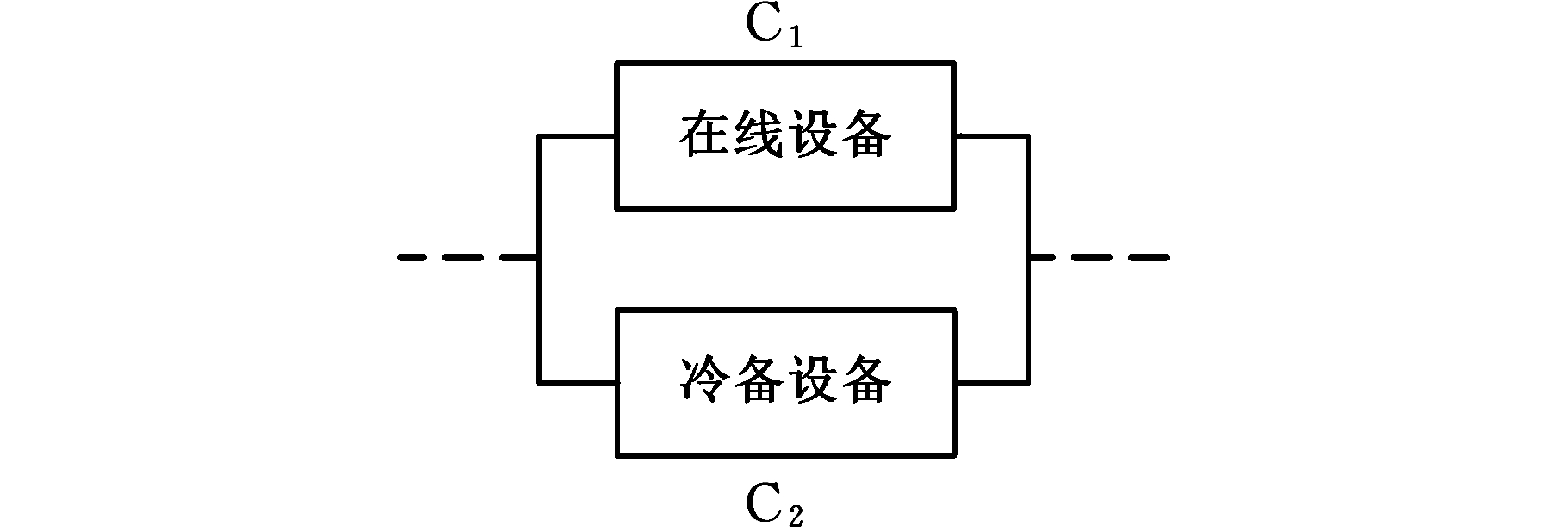
图1 系统结构图
Fig.1 Structure of the system
为了有效地建立冷备系统的维护模型,作如下合理的假设:
(1)初始状态下系统为全新,一个部件进入工作状态,另一个部件处于冷备状态。
(2)当一个部件处于失效状态或者预防性维护状态时,冷备部件立即进入工作状态。
(3)经过维修或者预防性维护后,部件恢复到全新状态。并且,根据另外一个部件的状态,该部件进入工作状态或者冷备状态。小修、大修及预防性维护的时间是独立的。
(4)只有一个维修人员,维修和预防性维护遵循先进先出的原则。当在线部件失效,并且闲置部件刚好不可用时,系统失效。
基于上述假设,将部件C1和部件C2的状态分别记为![]() 和
和![]() 其中0表示部件处于运行状态,1表示部件处于冷备并可用状态,2表示部件处于随机失效后进入小修状态,3表示部件处于退化失效后进入大修状态,4表示部件处于预防性维护状态。那么,系统的运行渐进过程和状态转移过程可分别由图2和图3表示。其中,S0、S1、S2、S3及S4为系统的各个状态,对系统各个状态作如下定义:S0表示系统的初始状态;S1表示在线部件随机失效,并进入小修状态,冷备部件立即进入工作状态;S2表示在线部件退化失效并进入大修状态,冷备部件立即进入工作状态;S3表示在线部件进入预防性维护状态,冷备部件立即进入工作状态;S4表示在线部件失效,但另外一个设备正处于不可用状态(小修、大修或者预防性维护)。
其中0表示部件处于运行状态,1表示部件处于冷备并可用状态,2表示部件处于随机失效后进入小修状态,3表示部件处于退化失效后进入大修状态,4表示部件处于预防性维护状态。那么,系统的运行渐进过程和状态转移过程可分别由图2和图3表示。其中,S0、S1、S2、S3及S4为系统的各个状态,对系统各个状态作如下定义:S0表示系统的初始状态;S1表示在线部件随机失效,并进入小修状态,冷备部件立即进入工作状态;S2表示在线部件退化失效并进入大修状态,冷备部件立即进入工作状态;S3表示在线部件进入预防性维护状态,冷备部件立即进入工作状态;S4表示在线部件失效,但另外一个设备正处于不可用状态(小修、大修或者预防性维护)。
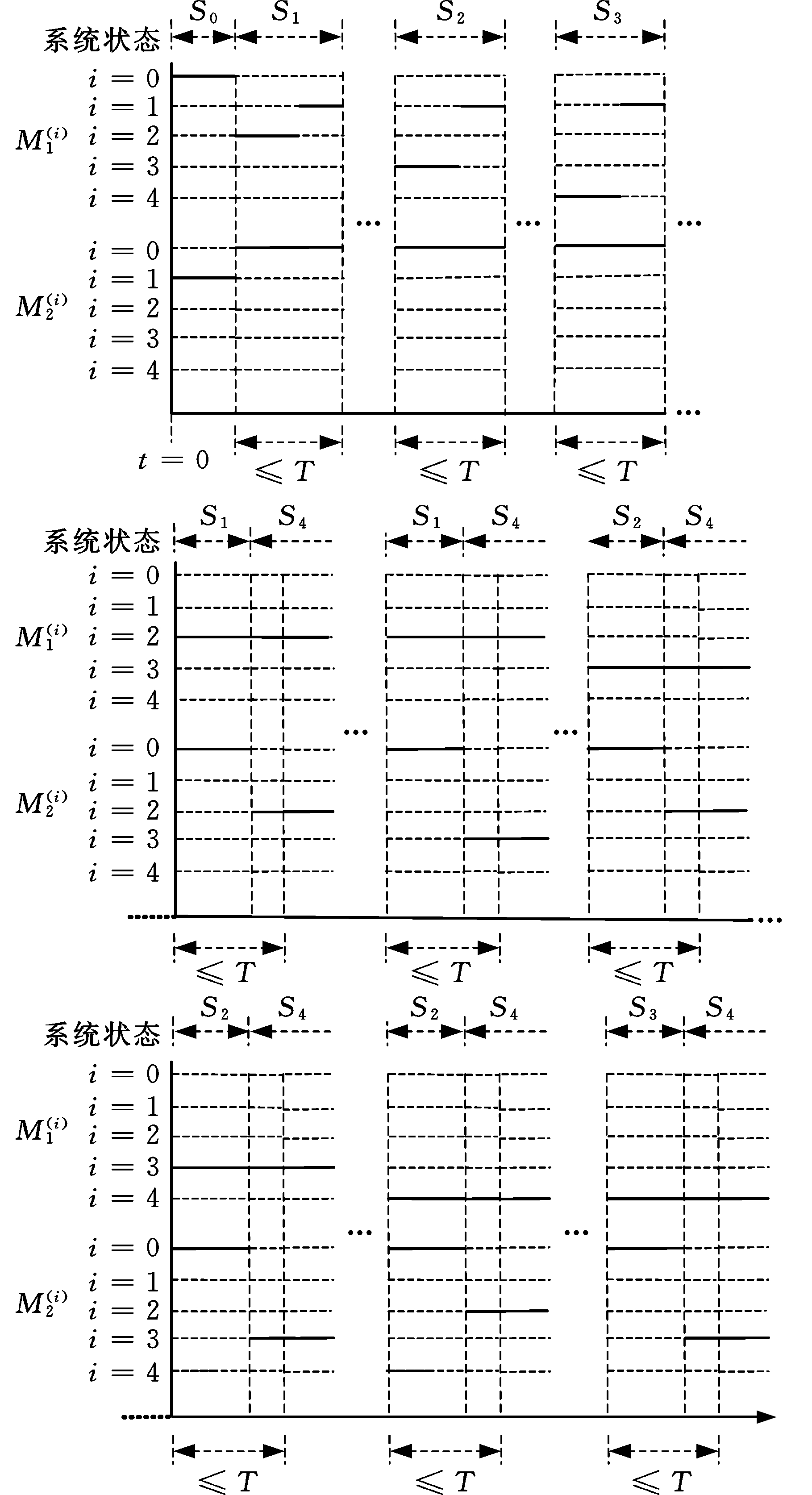
图2 系统运行渐进图
Fig.2 Progressive chart of the system

图3 系统状态转移图
Fig.3 State transition diagram of the system
2 预防性维护建模
令E表示系统的状态空间,E={Si|i=1,2,…,12},Tn表示系统进入任意状态Si的时刻点,Tn∈[0,∞),Zn表示时间段[Tn,Tn+1)之内的系统状态,那么{Zn,Tn|i=1,2,…}表示以E为状态空间的Markov更新过程,并且有
Pi,j(t)=P(Zn+1=j,Tn+1-Tn≤t|Zn=i)
(1)
即半马尔可夫内核。令随机变量XT表示预防性维护的时刻,其分布函数表示为
(2)
令Pi,j(t)表示系统从状态Si转移到状态Sj转移概率的CDF;XR表示随机失效时间;XD表示退化失效时间;YR表示小修时间;YD表示大修时间;YM表示预防性维护时间。根据系统状态转移规律,得到系统状态转移概率函数:
P0,1(t)=P(X1≤t,X1![]()
(3)
P0,2(t)=P(X2≤t,X2![]()
(4)
P0,3(t)=P(XT≤t,XT![]()
(5)
Pi,1(t)=P(X1≤t,Yi≤X1![]()
(6)
Pi,2(t)=P(X2≤t,Yi≤X2![]()
(7)
Pi,3(t)=P(XT≤t,Yi≤XT
P(Yi≤t,XT≤Yi![]()
![]()
(8)
Pi,4(t)=P(X1≤t,X1
P(X2≤t,X2![]()
![]()
(9)
P3,1(t)=P(X1≤t,YM≤X1![]()
(10)
P3,2(t)=P(X2≤t,YM≤X2![]()
(11)
P3,3(t)=P(XT≤t,YM≤XT
P(YM≤t,XT≤YM![]()
![]()
(12)
P3,4(t)=P(X1≤t,X1
P(X2≤t,X2
(13)
3 预防性维护策略求解
3.1 系统平均首次失效时间
分析系统的状态转移概率函数可知,预防性维护的周期T与系统的状态转移概率密切相关,进而影响系统的平均失效时间。令πi(t)(i=0,1,2,3)表示系统从状态Si开始到失效的时间的CDF;ζi(t)=π′i(t)表示πi(t)的概率密度函数(probability density function,PDF);mi表示系统从状态Si开始到失效的平均失效时间;*表示卷积;∧表示拉氏变换的结果。依据更新过程理论,对Pi,j(t)与πi(t)作卷积,可得马尔可夫更新方程组:
π0(t)=P0,1(t)*π1(t)+P0,2(t)*π2(t)+
P0,3(t)*π3(t)
(14)
π1(t)=P1,4(t)+P1,5(t)+P1,1(t)*π1(t)+
P1,2(t)*π2(t)+P1,3(t)*π3(t)
(15)
π2(t)=P2,6(t)+P2,7(t)+P2,1(t)*π1(t)+
P2,2(t)*π2(t)+P2,3(t)*π3(t)
(16)
π3(t)=P3,8(t)+P3,9(t)+P3,1(t)*π1(t)+
P3,2(t)*π2(t)+P3,3(t)*π3(t)
(17)
对式(14)~式(17)先微分再进行拉氏变换,得到
∧ζ0(S)=∧P0,1(S)·∧ζ1(S)+
∧P0,2(S)·∧ζ2(S)+∧P0,3(S)·∧ζ3(S)
(18)
∧ζ1(S)=∧P′1,4(S)+∧P′1,5(S)+
∧P1,1(S)·∧ζ1(S)+∧P1,2(S)·∧ζ2(S)+
∧P1,3(S)·∧ζ3(S)
(19)
∧ζ2(S)=∧P′2,6(S)+∧P′2,7(S)+
∧P2,1(S)·∧ζ1(S)+∧P2,2(S)·∧ζ2(S)+
∧P2,3(S)·∧ζ3(S)
(20)
∧ζ3(S)=∧P′3,8(S)+∧P′3,9(S)+
∧P3,1(S)·∧ζ1(S)+∧P3,2(S)·∧ζ2(S)+
∧P3,3(S)·∧ζ3(S)
(21)
由于
mi=![]() tdπi(t)=
tdπi(t)=![]() tζi(t)dt=
tζi(t)dt=![]()
(22)
所以,由式(18)~式(21)可得线性方程组:
m0=τ0+∧P0,1(0)m1+∧P0,2(0)m2+∧P0,3(0)m3
(23)
m1=τ1+∧P1,1(0)m1+∧P1,2(0)m2+∧P1,3(0)m3
(24)
m2=τ2+∧P2,1(0)m1+∧P2,2(0)m2+∧P2,3(0)m3
(25)
m3=τ3+∧P3,1(0)m1+∧P3,2(0)m2+∧P3,3(0)m3
(26)
τ0、τ1、τ2、τ3具有如下形式:
τ0=-(∧P′0,1(0)+∧P′0,2(0)+∧P′0,3(0))
(27)
τ1=-(∧P′1,1(0)+∧P′1,2(0)+∧P′1,3(0)-∧P″1,4(0))
(28)
τ2=-(∧P′2,1(0)+∧P′2,2(0)+∧P′2,3(0)-∧P2,4(0))
(29)
τ3=-(∧P′3,1(0)+∧P′3,2(0)+∧P′3,3(0)-∧P″3,4(0))
(30)
其中,∧P′i,j表示对∧Pi,j求一阶导,∧P″i,j表示对∧Pi,j求二阶导。
令∧Pi,j=∧Pi,j(0),通过解式(23)~式(26),得
η=(1-∧P3,3){∧P0,1[(1-∧P2,2)(1-∧P3,3)-
∧P2,3∧P3,2]+∧P0,2[∧P2,1(1-∧P3,3)+
∧P2,3∧P3,1]+∧P0,3[∧P3,1(1-∧P2,2)+
∧P2,1∧P3,2]}τ1+(1-∧P3,3){∧P0,1[∧P1,2(1-
∧P3,3)+∧P1,3∧P3,2]+∧P0,2[(1-∧P1,1)(1-
∧P3,3)-∧P1,3∧P3,1]+∧P0,3[∧P3,2(1-
∧P1,1)+∧P1,2∧P3,1]}τ2+(1-
∧P3,3){∧P0,1[∧P1,3(1-∧P2,2)+∧P1,2∧P2,3]+
∧P0,2[∧P2,3(1-∧P1,1)+∧P1,3∧P2,1]+
∧P0,3[(1-∧P1,1)(1-∧P2,2)-∧P1,2∧P2,1]}τ3+
{[(1-∧P1,1)(1-∧P3,3)-∧P1,3∧P3,1][(1-
∧P2,2)(1-∧P3,3)-∧P2,3∧P3,2]-[∧P1,2(1-
∧P3,3)+∧P1,3∧P3,2][∧P2,1(1-∧P3,3)+
∧P2,3∧P3,1]}τ0
θ=[(1-∧P1,1)(1-∧P3,3)-∧P1,3∧P3,1][(1-
∧P2,2)(1-∧P3,3)-∧P2,3∧P3,2]-
[∧P1,2(1-∧P3,3)+∧P1,3∧P3,2][∧P2,1(1-
∧P3,3)+∧P2,3∧P3,1]
显然,m0是关于T的函数,所以将其化简为m0(T),通过解m0(T)的最大值可求得最佳预防性维护周期T*。
3.2 系统稳态可用度
令Ai(t)表示系统在时刻t处于状态Si的CDF,ai(t)表示系统在时刻t处于状态Si的PDF,可得系统可用度更新方程组:
A0(t)=P0,1(t)*A1(t)+P0,2(t)*A2(t)+
P0,3(t)*A3(t)
(31)
A1(t)=ν1+P1,1(t)*A1(t)+P1,2(t)*A2(t)+
P1,3(t)*A3(t)
(32)
A2(t)=ν2+P2,1(t)*A1(t)+P2,2(t)*A2(t)+
P2,3(t)*A3(t)
(33)
A3(t)=ν3+P3,1(t)*A1(t)+P3,2(t)*A2(t)+
P3,3(t)*A3(t)
(34)
其中, ν1(t)、ν2(t)、ν3(t)具有如下形式:
(35)
(36)
(37)
由于
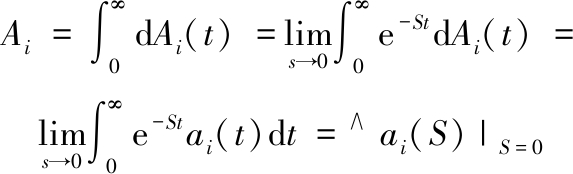
(38)
所以,由式(31)~式(34)可得线性方程组:
A0=∧P0,1(0)·A1+∧P0,2(0)·A2+∧P0,3(0)·A3
(39)
A1=∧ν′1(0)+∧P1,1(0)·A1+∧P1,2(0)·A2+
∧P1,3(0)·A3
(40)
A2=∧ν′2(0)+∧P2,1(0)·A1+∧P2,2(0)·A2+
∧P2,3(0)·A3
(41)
A3=∧ν′3(0)+∧P3,1(0)·A1+∧P3,2(0)·A2+
∧P3,3(0)·A3
(42)
令∧Pi,j=∧Pi,j(0),通过解式(39)~式(42),得
γ=(1-∧P3,3){∧P0,1[(1-∧P2,2)(1-∧P3,3)-
∧P2,3∧P3,2]+∧P0,2[P2,1(1-∧P3,3)+
∧P2,3∧P3,1]+∧P0,3[∧P3,1(1-∧P2,2)+
∧P2,1∧P3,2]}∧ν′1(0)+(1-
∧P3,3){∧P0,1[∧P1,2(1-∧P3,3)+∧P1,3∧P3,2]+
∧P0,2[(1-∧P1,1)(1-∧P3,3)-∧P1,3∧P3,1]+
∧P0,3[∧P3,2(1-∧P1,1)+∧P1,2∧P3,1]}∧ν′2(0)+(1-
∧P3,3){∧P0,1[∧P1,3(1-∧P2,2)+∧P1,2∧P2,3]+
∧P0,2[∧P2,3(1-∧P1,1)+∧P1,3∧P2,1]+
∧P0,3[(1-∧P1,1)(1-P2,2)-∧P1,2∧P2,1]}∧ν′3(0)
ψ=[(1-∧P1,1)(1-∧P3,3)-∧P1,3∧P3,1][(1-
∧P2,2)(1-∧P3,3)-∧P2,3∧P3,2]-[∧P1,2(1-
∧P3,3)+∧P1,3∧P3,2][(∧P2,1(1-∧P3,3)+∧P2,3∧P3,1]
显然,A0也是关于T的函数,所以将其化简为A0(T),通过解A0(T)的最大值可求得最佳预防性维护周期T*。
4 实例分析
以某小型污水泵站的污水泵为研究对象,对其进行可靠性研究。已知污水泵站的工作环境比较恶劣,为了提高污水泵站的可靠性,现将原污水泵改装成由两台污水泵组成的冷备系统。根据污水泵的故障记录与维修记录,以平均值法获得本文维护模型的各参数。F1(t)、G1(t)、G2(t)、G3(t)分别符合参数为λ1、μ1、μ2、μ3的指数分布;F2(t)符合参数为α、λ2的威布尔分布。
采用表1所示的参数组合对冷备系统的首次平均失效时间进行分析,主要研究这个性能指标及其变化率与预防性维护周期T之间的关系,分析结果如图4和图5所示。图4描述了不同参数组合下系统首次平均失效时间与预防性维护周期T之间的关系。通过对曲线s1的分析,找到系统最大首次平均失效时间m0(0.4)=440,对应的最佳预防性维护周期T=0.4。换句话说,当所选参数为s1组参数,对在线设备作周期为0.4单位时间的预防性维护时,系统首次平均失效时间最长为440个单位时间。通过对比s1曲线与其他各组曲线可知,系统最大首次平均失效时间与最佳预防性维护周期总是随着μ1、μ2及μ3的增大而增大,但随着λ1和λ2的增大而减小。
表1 相关参数
Tab.1 Related parameters
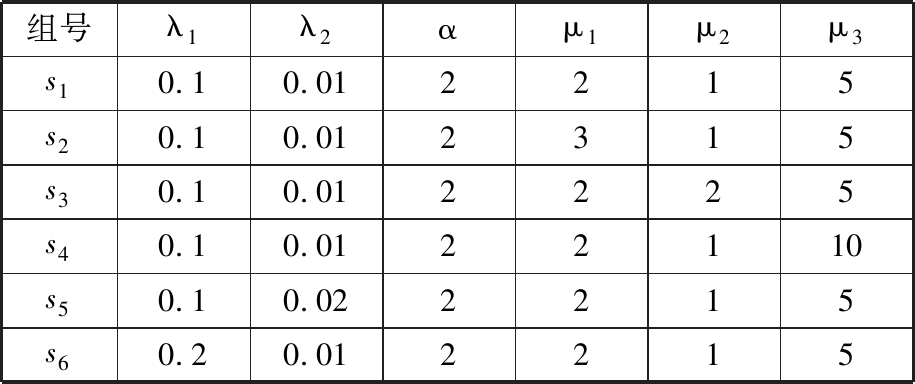
组号λ1λ2αμ1μ2μ3s10.10.012215s20.10.012315s30.10.012225s40.10.0122110s50.10.022215s60.20.012215
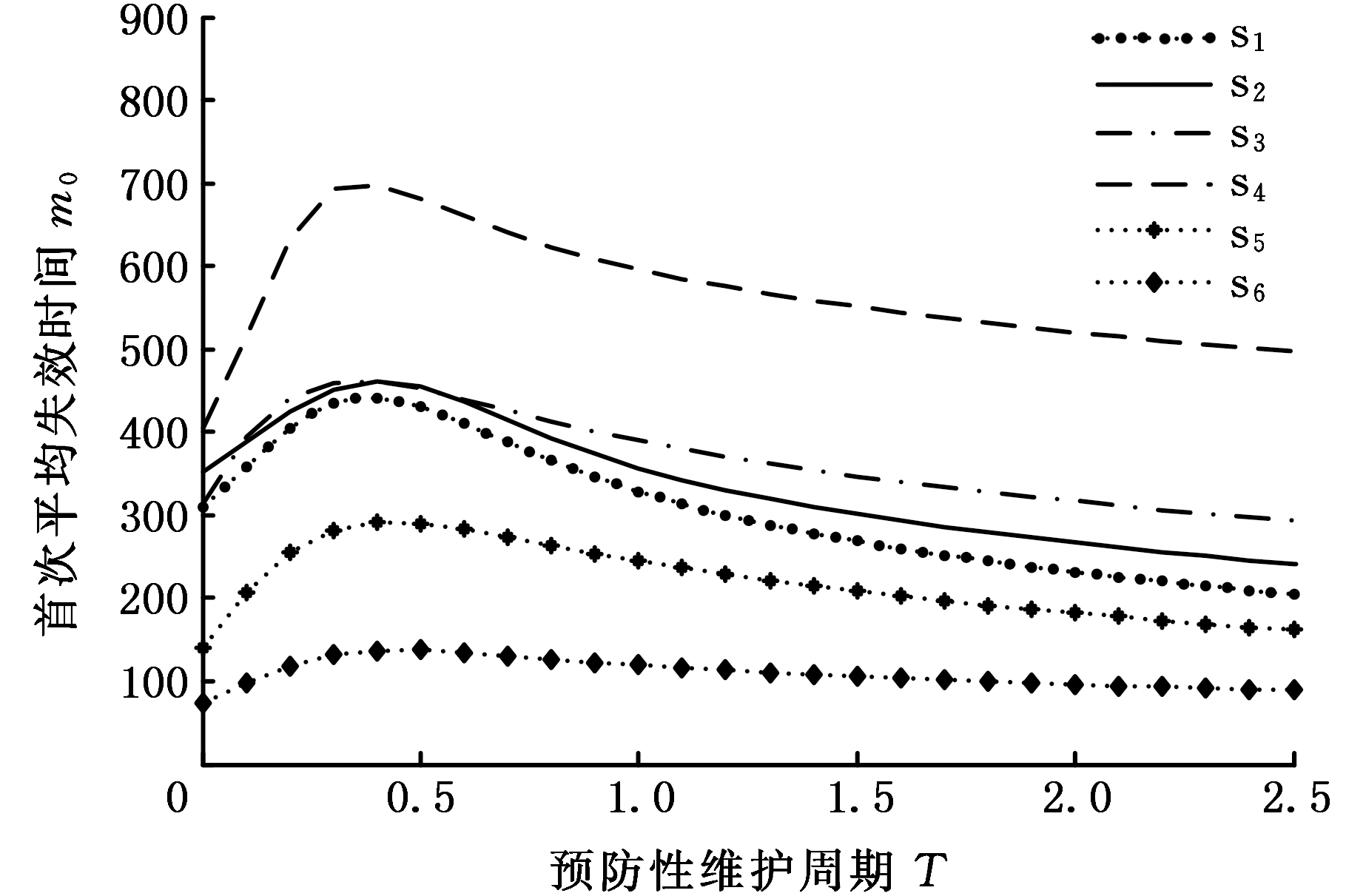
图4 首次平均失效时间与预防性维护周期
Fig.4 Mean time to the first system failure and preventive maintenance cycle
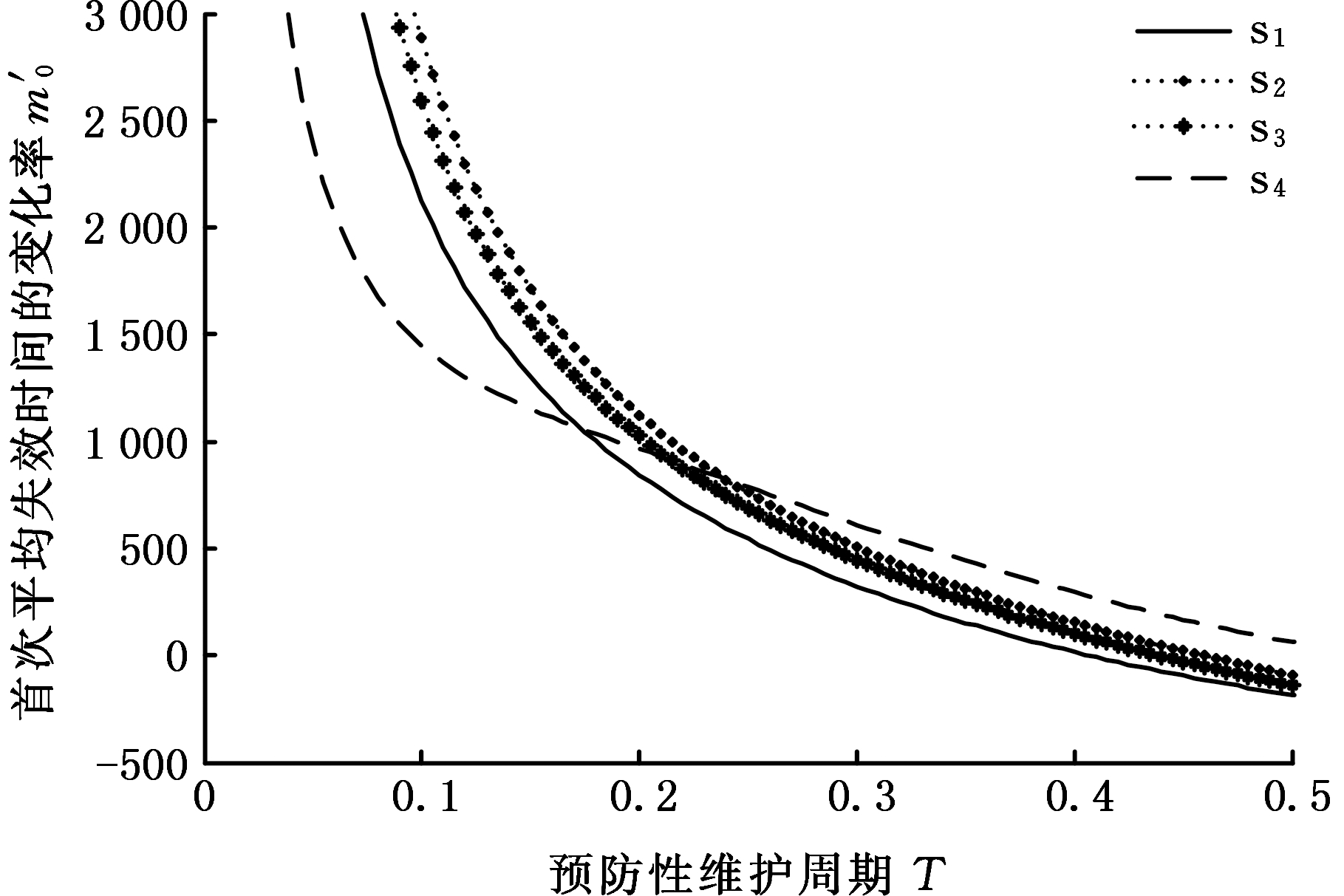
图5 首次平均失效时间的变化率与预防性维护周期
Fig.5 The varying rate of mean time to the first system failure and preventive maintenance cycle
图5描述了系统首次平均失效时间的变化率与预防性维护周期T之间的关系,主要是分析小修、大修及预防性维护对系统首次平均失效时间的影响程度。当固定λ1和λ2不变时,发现系统首次平均失效时间的变化率总是随着预防性维护周期T的增大而减小,说明小修、大修及预防性维护对提高系统首次平均失效时间具有促进作用。通过对比s1~s4曲线可知,随着T的增大,s1、s2、s3曲线斜率都先大于s4曲线斜率,当T继续增大后,s1、s2、s3曲线斜率都又小于s4曲线斜率。此外,s1、s2、s3曲线斜率的递减趋势非常接近,但曲线斜率的递减斜率总大于s4曲线的递减斜率,这个现象说明预防性维护对延迟系统首次失效作用最大。
同样采用表1所示参数组合对冷备系统稳态可用度进行分析,主要研究这个性能指标及其变化率与预防性维护周期T之间的关系,分析结果如图6和图7所示。
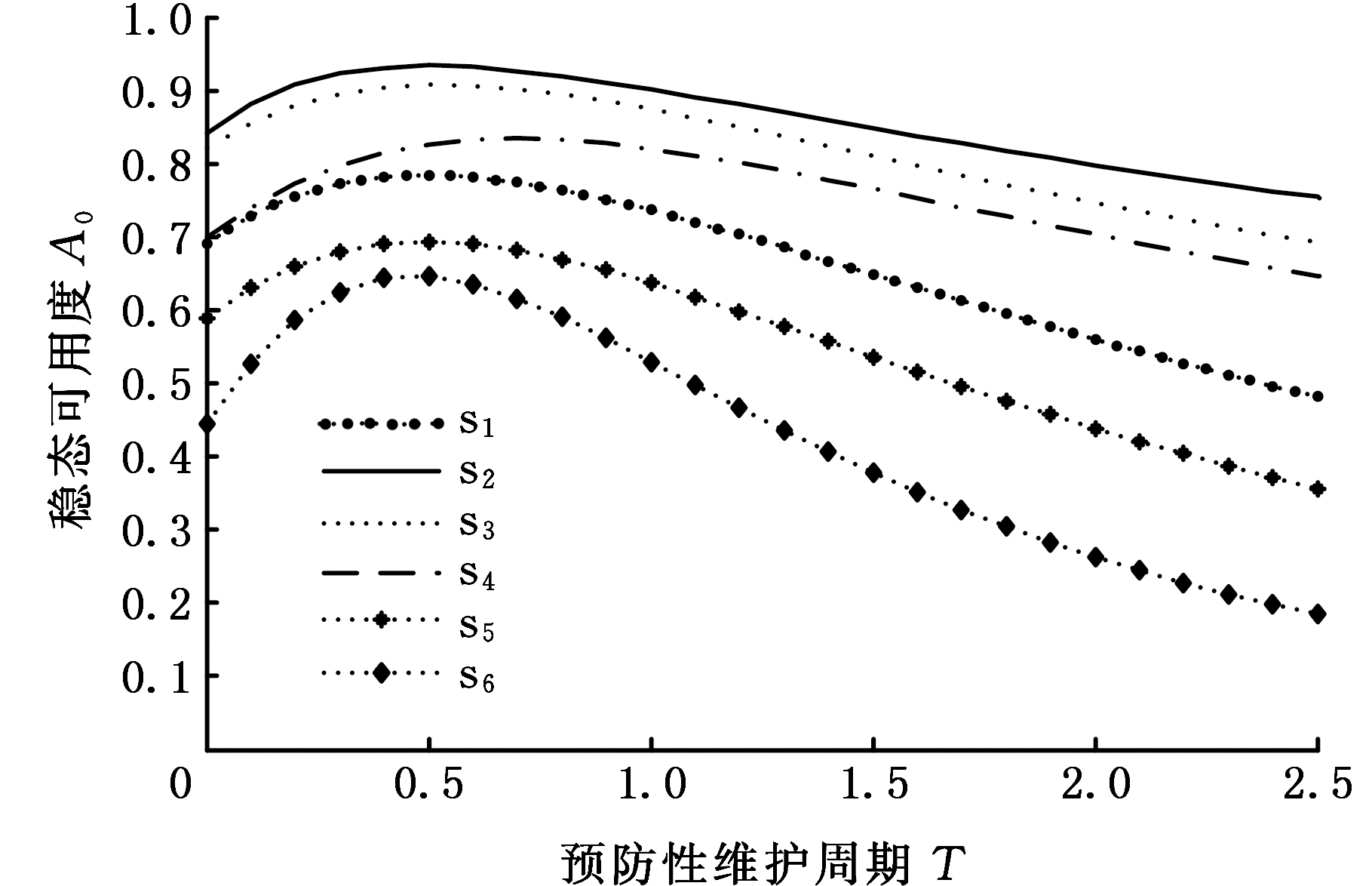
图6 稳态可用度与预防性维护周期的关系
Fig.6 Steady state availability and preventive maintenance cycle
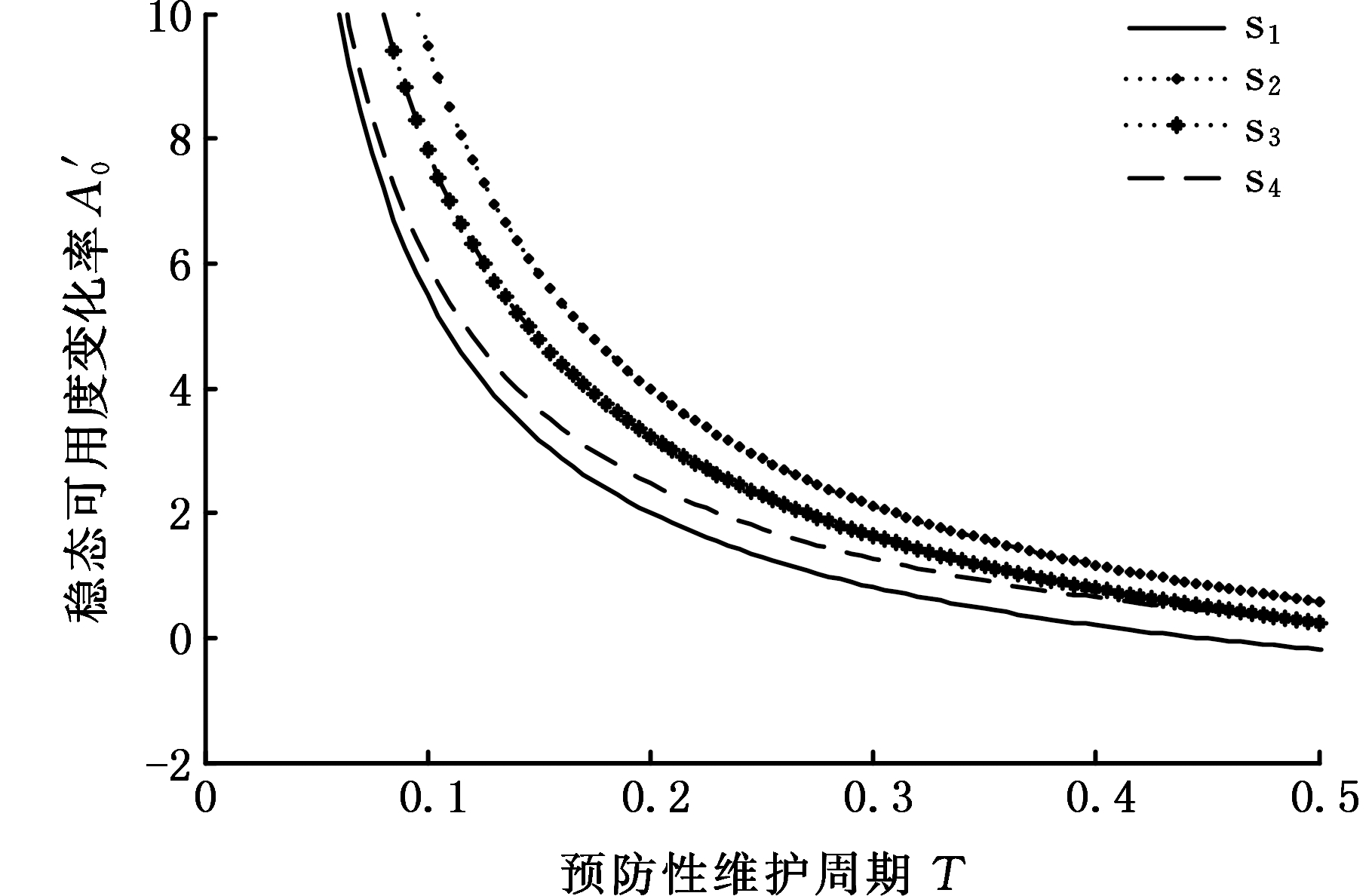
图7 稳态可用度变化率与预防性维护周期的关系
Fig.7 The varying rate of steady state availability and preventive maintenance cycle
图6反映了系统稳态可用度与预防性维护周期T之间的关系。通过对曲线s1的分析可知,当预防性维护周期为0.5个单位时间时,系统稳态可用度最大,其值为0.78。通过对比s1曲线与其他各组曲线可知,系统最大稳态可用度及最佳预防性维护周期随着μ1、μ2及μ3的增大而增大,但随着λ1和λ2的增大而减小。
图7描述了系统稳态可用度的变化率与预防性维护周期T之间的关系。当λ1和λ2固定不变时,发现系统稳态可用度的变化率总是随着预防性维护周期T的增大而减小,这也说明,小修、大修及预防性维护对提高系统的稳态可用度具有促进作用。通过对比s1~s4曲线可知,四条曲线位置从上到下依次为s2、s3、s4和s1,但曲线斜率的递减趋势都比较接近,这个现象可以说明,如果以稳态可用度为追求目标,则随机失效率的变化对系统长期运行的可靠性影响不大。
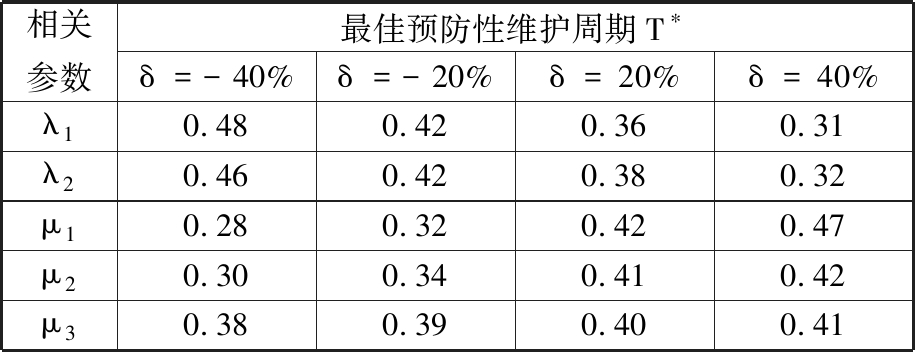
为了进一步比较各参数对预防性维护周期T的影响程度,分别选取系统首次平均失效时间和稳态可用度作为目标函数,分析所有参数对预防性维护周期T的敏感度。以s1组参数为原始参数,每次分析时选取其中一个参数,然后对该参数分别以-40%、-20%、20%、40%的变化幅度(δ)进行取值,与此同时,其他参数取值保持不变。首先选取系统首次平均失效时间为目标函数,作最佳预防性维护周期T*的参数敏感度分析,分析结果如表2所列,并且其相互关系如图8所示。
表2 对最佳预防性维护周期的参数敏感度分析
(以首次平均失效时间为性能指标)
Tab.2 Parameter sensitivity analysis for the optimal preventive maintenance cycle(taking the mean time to the first system failure as the performance index)
相关参数最佳预防性维护周期T∗δ=-40%δ=-20%δ=20%δ=40%λ10.480.420.360.31λ20.460.420.380.32μ10.280.320.420.47μ20.300.340.410.42μ30.380.390.400.41
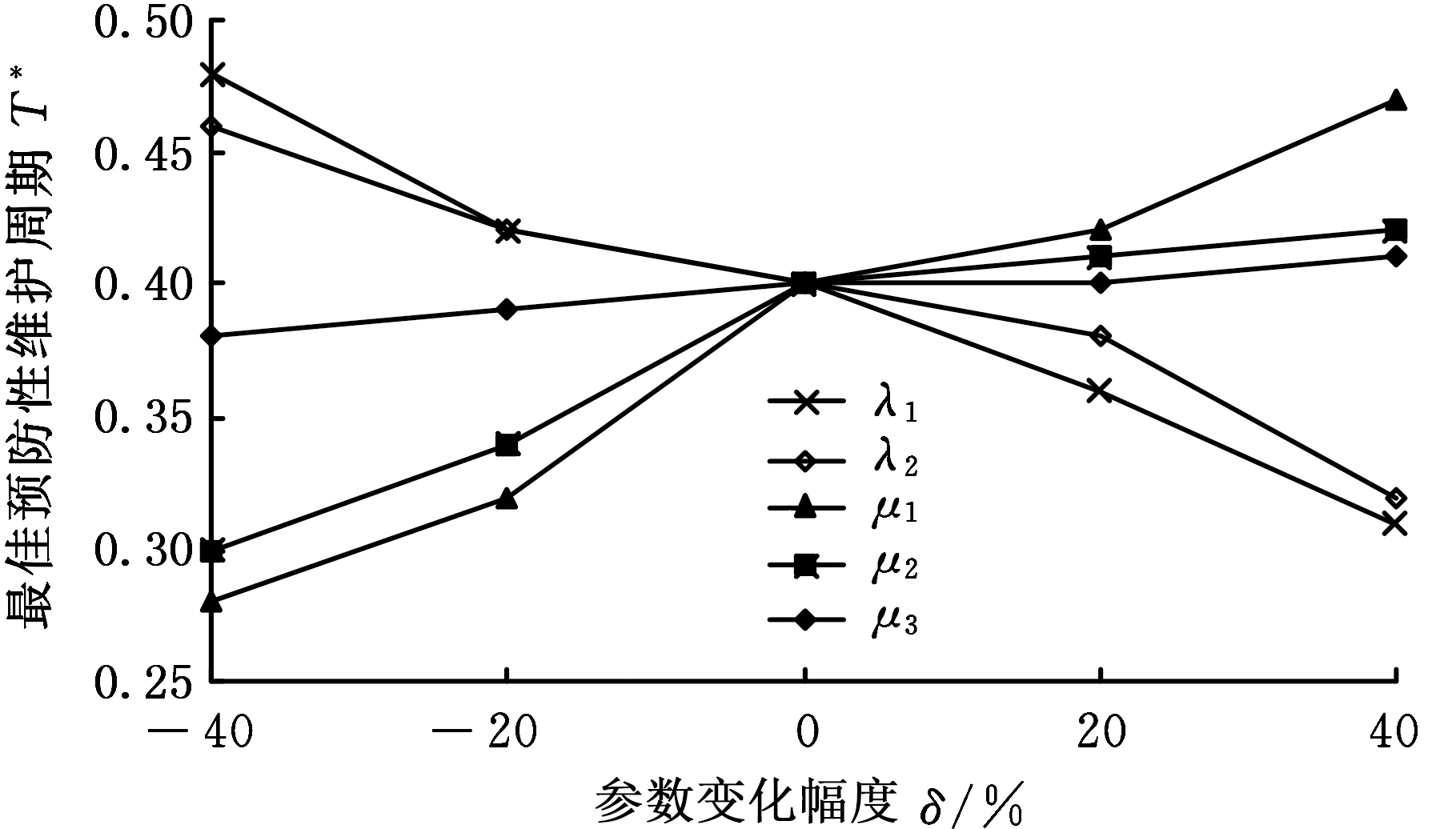
图8 参数变化对最佳预防性维护周期的影响(以首次平均失效时间为性能指标)
Fig.8 The influence of parameters on the optimal maintenance cycle(taking the mean time to the first system failure as the performance index)
图8描述的是以系统首次平均失效时间为性能指标时,各参数变化对最佳预防性维护周期T*的影响情况。从图中可知,系统最佳预防性维护周期T*对λ1、λ2和μ1的变化最敏感,对参数μ2的变化中等敏感,对参数μ3的变化略不敏感。其中,最佳预防性维护周期T*随着λ1、λ2的增大而减小,随着μ1、μ2、μ3的增大而增大。显而易见,随着λ1、λ2的增大,在线设备容易发生故障,那么为了降低系统失效风险,需要加大对在线设备预防性维护频率。此外,μ1也是一个影响最佳预防性维护周期的重要参数。随机失效小修的效率高,在线设备发生随机失效后,维护人员能够在较短时间内完成修复,从而降低系统失效风险。
同理,选取系统稳态可用度作为性能指标,分析所有参数对预防性维护周期T的敏感度,分析结果如表3所列,并且其相互关系如图9所示。
表3 对最佳预防性维护周期的参数敏感度分析(以系统稳态可用度为性能指标)
Tab.3 Parameter sensitivity analysis for the optimal preventive maintenance cycle(taking the steady-state availability of the system as the performance index)
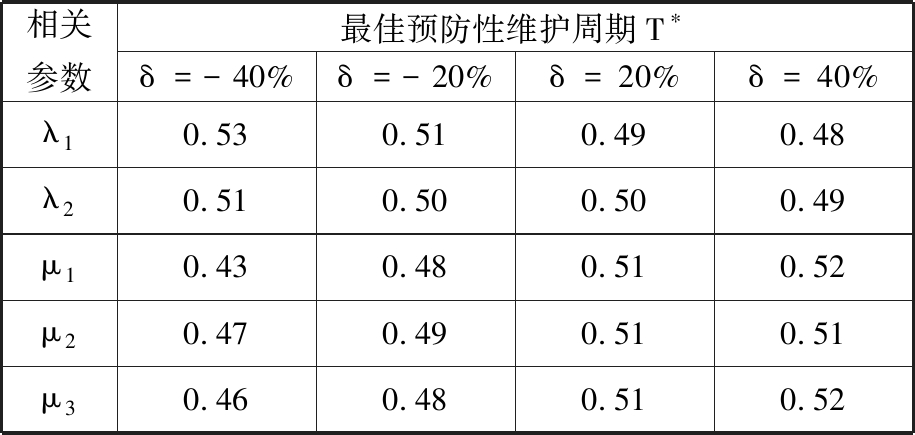
相关参数最佳预防性维护周期T∗δ=-40%δ=-20%δ=20%δ=40%λ10.530.510.490.48λ20.510.500.500.49μ10.430.480.510.52μ20.470.490.510.51μ30.460.480.510.52
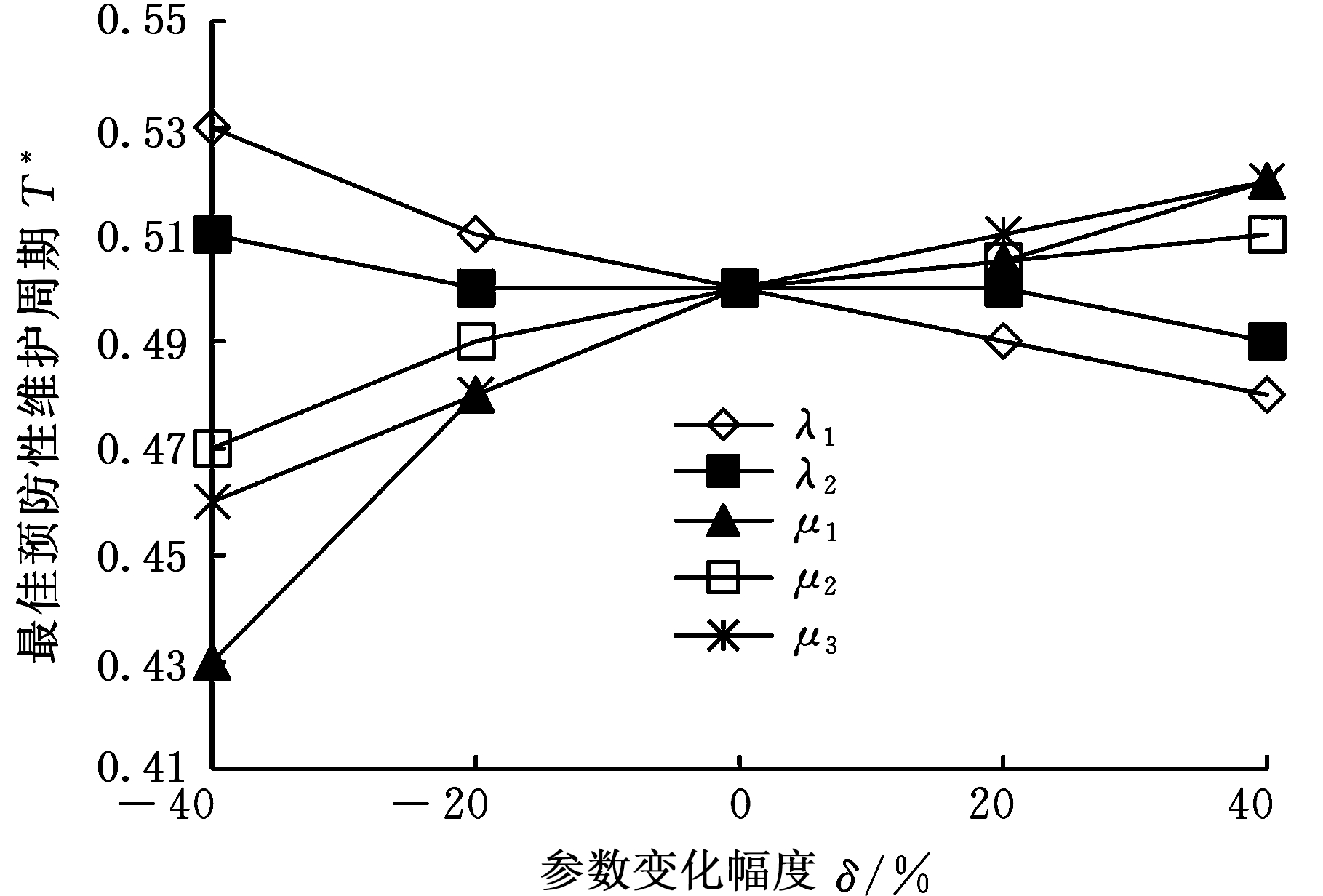
图9 参数变化对最佳预防性维护周期的影响(以系统稳态可用度为性能指标)
Fig.9 The influence of parameters on the optimal maintenance cycle(taking the steady-state availability of the system as the performance index)
图9描述的是以系统稳态可用度为性能指标时,各参数变化对最佳预防性维护周期T*的影响情况。从图中可知,系统最佳预防性维护周期T*对参数μ1和λ1的变化较敏感,对参数μ3的变化中等敏感,对其他参数的变化略不敏感。其中,最佳预防性维护周期T*随着λ1的增大而减小,这说明较大随机失效率带来了冷备系统意外失效风险。一般情况下,为了保障系统可靠性,需要加大预防性维护频率。从图9中不难发现,最佳预防性维护周期T*对μ1的变化最敏感,说明了随机失效小修的效率提高,较少的预防性维护就能够保障系统安全。对比图8和图9可知,对于冷备系统来说,预防性维护对系统稳态可用度的影响大于其对系统首次平均失效时间的影响。
总之,相对退化失效过程来说,随机失效过程及小修对冷备系统的首次平均失效时间与稳态可用度的影响较大;相对系统稳态可用度来说,退化失效过程对系统首次平均失效时间的影响较大;相对系统首次平均失效时间来说,预防性维护对提高系统稳态可用度的作用更大。
5 结束语
本文提出了一种考虑两种失效形式的两机冷备系统的预防性维护建模方法。分别以系统首次平均失效时间与可用度为优化目标求解最佳预防性维护策略。通过实例分析及参数敏感性分析验证了本文所提建模方法的有效性,并揭示了随机失效过程、退化失效过程以及预防性维护对两个可靠性指标的不同影响规律。该建模方法能够为实际工程领域中关键设备维护决策的制定提供新思路。另外,本文将维护人员的响应时间忽略,这与实际生产情况存在差异,因此,目前笔者正在开展考虑维护人员响应时间的冷备系统维护决策的研究。
[1] LIAO W Z, PAN E S, XI L F. Preventive Maintenance Scheduling for Repairable System with Deterioration[J]. Journal of Intelligent Manufacturing, 2010, 21(6): 875-884.
[2] 阮渊鹏, 李晓, 崔剑. 考虑不完全保护的复杂系统可靠性评估[J]. 中国机械工程, 2015, 26(22):3001-3007.
RUAN Yuanpeng, LI Xiao, CUI Jian. Reliability Evaluation of Complex System with Imperfect Protections[J]. China Mechanical Engineering, 2015, 26(22):3001-3007.
[3] 刘银华, 纪飞翔, 叶夏亮. 车身多工位装配系统可靠性评估与维护策略研究[J]. 中国机械工程, 2016, 27(2): 273-277.
LIU Yinhua, JI Feixiang, YE Xialiang. Study on Reliability Evaluation and Maintenance Policy of Auto Body Multi-station Assembly System[J]. China Mechanical Engineering, 2016, 27(2): 273-277.
[4] ZHOU X, HUANG K, XI L, et al. Preventive Maintenance Modeling for Multi-component Systems with Considering Stochastic Failures and Disassembly Sequence[J]. Reliability Engineering and System Safety, 2015, 142: 231-237.
[5] XIAO L, SONG S, CHEN X, et al. Joint Optimization of Production Scheduling and Machine Group Preventive Maintenance[J]. Reliability Engineering and System Safety, 2016, 146: 68-78.
[6] YANG L, ZHAO Y, PENG R, et al. Hybrid Preventive Maintenance of Competing Failures under Random Environment[J]. Reliability Engineering and System Safety, 2018, 174:130-140.
[7] COIT D W. Cold-standby Redundancy Optimization for Nonrepairable Systems[J]. IIE Transactions, 2001, 33(6): 471-478.
[8] ZHANG Y L, WANG G J. A Bivariate Optimal Repair-replacement Model Using Geometric Processes for a Cold Standby Repairable System[J]. Engineering Optimization, 2006, 38(5): 609-619.
[9] WU Q T, WU S M. Reliability Analysis of Two-unit Cold Standby Repairable Systems under Poisson Shocks[J]. Applied Mathematics and Computation, 2011, 218(1): 171-182.
[10] ZHONG C Q, JIN H B. A Novel Optimal Preventive Maintenance Policy for a Cold Standby System Based on Semi-Markov Theory[J]. European Journal of Operational Research, 2014, 232(2): 405-411.
[11] JIA J S, WU S M. Optimizing Replacement Policy for a Cold-standby System with Waiting Repair Times[J]. Applied Mathematics and Computation, 2009, 214(1): 133-141.
[12] LEUNG K N F, ZHANG Y L, LAI K K. Analysis for a Two-dissimilar-component Cold Standby Repairable System with Repair Priority[J]. Reliability Engineering and System Safety, 2011, 96(11): 1542-1551.
[13] ZHANG Y L, WANG G J. A Geometric Process Repair Model for a Repairable Cold Standby System with Priority in Use and Repair[J]. Reliability Engineering and System Safety, 2017, 94(11): 1782-1787.
