0 引言
以气体作为润滑介质的推力轴承和气膜端面密封具有低摩擦阻力、高精度、污染小和长使用寿命的特点,在高速旋转机械轴端和高精度加工设备上得到广泛应用。为保证两相对运转端面之间有一层稳定的微米级气膜,在摩擦副的某一端面上需开设能产生流体动静压效应的结构,如动压浅槽、节流孔或微孔织构等,其中以对数螺旋槽为代表的动压浅槽结构应用最广。
对数螺旋槽具有强流体动压效应和高气膜稳定性,是干气密封[1]和气体推力轴承端面结构的首选端面结构,但目前并没有明确的分析表明对数螺旋线在任何条件下都是最优的端面型槽型线。近几十年来,国内外学者一直在探索将其他经典几何型线作为端面型槽型线的可能性。SALANT等[2]、LIU等[3]对比分析了斜直线槽与螺旋槽的机械密封和推力轴承的泄漏和承载特性,指出型线对端面流场的影响明显。吴宗祥等[4]、CHEN等[5]、胡丹梅等[6]分别对比分析了直线槽、超椭圆曲线槽和圆弧槽的气膜密封与螺旋槽气膜密封的稳动态特性,指出直线槽适用于低速条件。经典的几何型线具有数学方程明确、模型描述方便等优点,但受限于型线数学模型的固有特性,难以实现端面密封和推力轴承承载特性与气膜稳定性的进一步提升。
近年来,随着智能优化算法的发展,国内外学者采用遗传算法、SQP等方法对端面型槽进行形状优化,获得了不同条件下端面型槽的最佳形状。HASHIMOTO[7]、SHEN等[8]、魏超等[9]以样条曲线表征型槽型线,采用智能优化算法对气体推力轴承和液体机械密封的型线进行优化,以期获得最大的承载力和流体膜刚度;许鹏先等[10]、丁雪兴等[11]则以流体流线的拟合曲线为型槽型线,获得了以5次多项式表达的最佳型槽型线。样条曲线和多项式的数学模型比较复杂,且不具典型性,构造表征能力更强的型线通用数学模型还有待进一步探索。
在对数螺旋线基础上,笔者提出了一种几何表征能力更强的广义对数螺旋线,并获得了斜直线、圆弧线、抛物线和椭圆线等经典几何型线的广义对数螺旋线表征方程,对比分析了广义对数螺旋角的分布和变化幅值对广义对数螺旋槽气体轴承承载力和气膜刚度的影响规律。
1 分析模型
1.1 广义对数螺旋线的通用方程
对数螺旋线的极坐标方程为
r=r0exp(θtanβ)
(1)
式中,r为极径;r0为起始极径;β为螺旋角;θ为极径r处的对数螺旋线与起始点之间的周向夹角。
对数螺旋线的终止极径为
rn=r0exp(αtanβ)
(2)
式中,α为对数螺旋线起始点与终止点之间的周向夹角,也称为极角。
定义任一型线在周向角θ处的切线与该点圆周线切线之间所夹的锐角为广义螺旋角β(θ)。理论上,任一连续光滑的型线都可看成是由无数段首尾相连的对数螺旋线微段组成的,统称为广义对数螺旋线。将广义对数螺旋线作为侧壁型线的端面型槽称为广义对数螺旋槽,其中,广义对数螺旋角沿周向恒为定值的对数螺旋槽是广义对数螺旋槽的一种特例。
图1a所示为典型的机械密封或推力轴承端面广义对数螺旋槽的几何结构。一个计算周期内,槽区和堰区的周向夹角分别为θg和θl,则槽宽堰宽比δ=θg/θl。图1b所示为广义对数螺旋线的几何结构和参数定义,可将广义对数螺旋线看成是由n段普通对数螺旋线组成的,则第i段对数螺旋线的极坐标方程为
(3)
(4)
式中,Δθi为第i段对数螺旋线起始点与终止点之间的周向夹角;![]() 为广义螺旋角。
为广义螺旋角。

(a) 广义对数螺旋槽

(b) 广义对数螺旋线
图1 广义对数螺旋线及广义螺旋角分布
Fig.1 Generalized logarithmic helix and generalized spiral angle distribution
为方便起见,将广义对数螺旋线看成是由n段周向等角度的普通对数螺旋线组成的,即将广义对数螺旋线周向n等分,则第i段对数螺旋线的Δθi=α/n。当对数螺旋线微段无穷多时,式(3)写成积分形式:
r=r0exp(![]() tanβdθ)
tanβdθ)
(5)
1.2 气膜承载特性求解模型
气体推力轴承端面间的流体可假设为层流、等温的等黏度气体,则计算轴承端面气膜压力的量纲一稳态Reynolds方程为
(6)
式中,p、h分别为端面任意点处的气膜压力和膜厚;pi为内径处压力;Λ为密封压缩数;ω为角速度;μ为气体黏度,下标i表示密封环内径的参数。
求解式(6)的强制性压力边界条件为:在轴承内径ri和外径ro处,Pin= Pout=1。周期性边界条件为P(θ+2π/Ng, R)=P(θ, R),其中,Ng为密封周期数。
图2为气膜压力分布和稳态性能计算的流程图,其中,κ、e分别为收敛因子和收敛残差,本文中取为-0.8和10-6,k为计算次数;下标i、j分别为密封端面周向和径向节点序号,m、n为密封端面单个计算的周期周向和径向网格数,本文中均取为150。采用有限差分法按照图2所示的程序流程求解式(6),获得端面压力分布,进而获得端面承载力F和轴向气膜刚度kz:
(7)
(8)
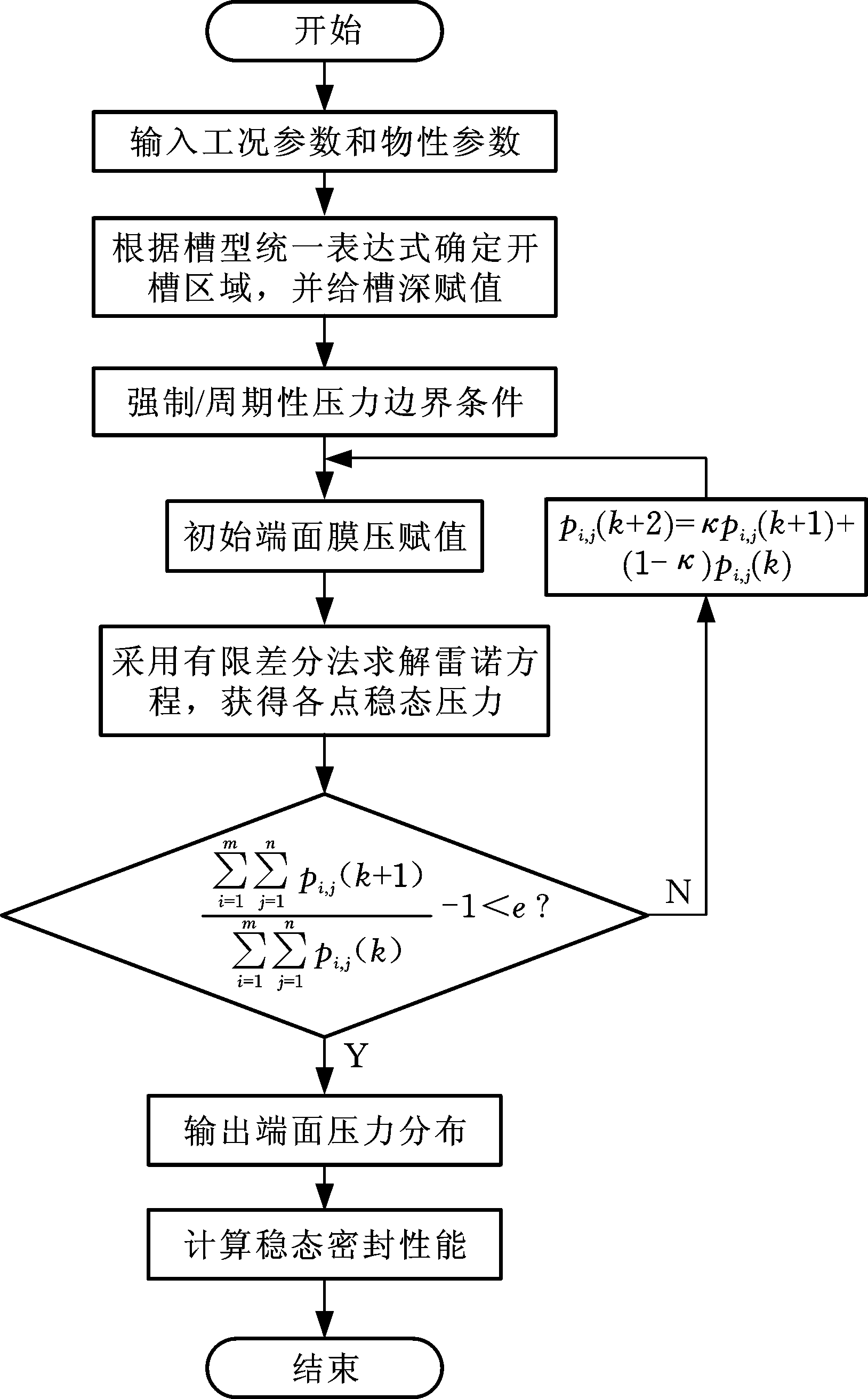
图2 气体轴承稳态性能求解流程图
Fig.2 Flow chart of steady-state performance calculation of gas bearing
2 结果分析与讨论
不同形状广义对数螺旋槽轴承性能对比时,对比基准对于对比结果至关重要,参与对比的不同广义对数螺旋槽型线的周向角度、周向开槽宽度和径向开槽宽度等参数相等。本文分析计算时采用的轴承几何结构参数和操作参数如下:轴承内径ri=80 mm,槽底半径rb=90 mm,轴承外径r0=100 mm,基准对数螺旋槽螺旋角β=15°,初始膜厚h0=3 μm,槽深hg=5 μm,槽宽堰宽比δ=1.0,转速n=10 000 r/min,轴承外径侧与内径侧压力都为大气压pa=101 kPa。
2.1 经典型线的广义对数螺旋线形式
直线、圆弧线、抛物线和椭圆线是几种经典的数学几何型线,国内外学者探讨了将上述经典几何型线作为机械密封或推力轴承端面型槽侧壁型线的可行性,推导了这4种经典几何型线的广义螺旋角形式,对比分析了将上述型线作为侧壁型线的广义对数螺旋槽推力轴承的承载特性[4,6]。
表1所示为4种几何型线的极坐标方程及其对应的广义螺旋角。图3所示为直线、圆弧线、抛物线、椭圆线和经典对数螺旋线的几何模型及对应的广义螺旋角分布,其中,A点、B点分别为几何型线的起始点和终止点。从终止半径rn(外径侧)至起始半径r0(内径侧),直线的广义螺旋角β(θ)呈单调递减分布,圆弧线的广义螺旋角β(θ)近似符合线性递增分布,抛物线的广义螺旋角β(θ)近似符合抛物线分布,椭圆线的广义螺旋角β(θ)近似符合对数分布。
表1 经典几何型线的极坐标方程及其广义螺旋角
Tab.1 Polar coordinate and generalize spiral angle of typical molded lines

型线类型极坐标方程r=φ(θ)广义螺旋角β(θ)直线r=rnr0sinαr0sinαcosθ-(rn-r0cosα)sinθarctanrn-r0cosαr0sinα-(α-θ)圆弧线(rsinθ-x0)2+(rcosθ-y0)2=r2o-arctanxr2o-x2-(α-θ)抛物线(r0cosα-rn)r2sin2θ+(r0sinα)2(rcosθ+rn)=0arctan2x(r0cosα-rn)(r0sinα)2-(α-θ)椭圆线(rsinθr0sinα)2+(rcosθ-r0cosαrn-r0cosα)2=1-arctanbxaa2-x2-(α-θ)
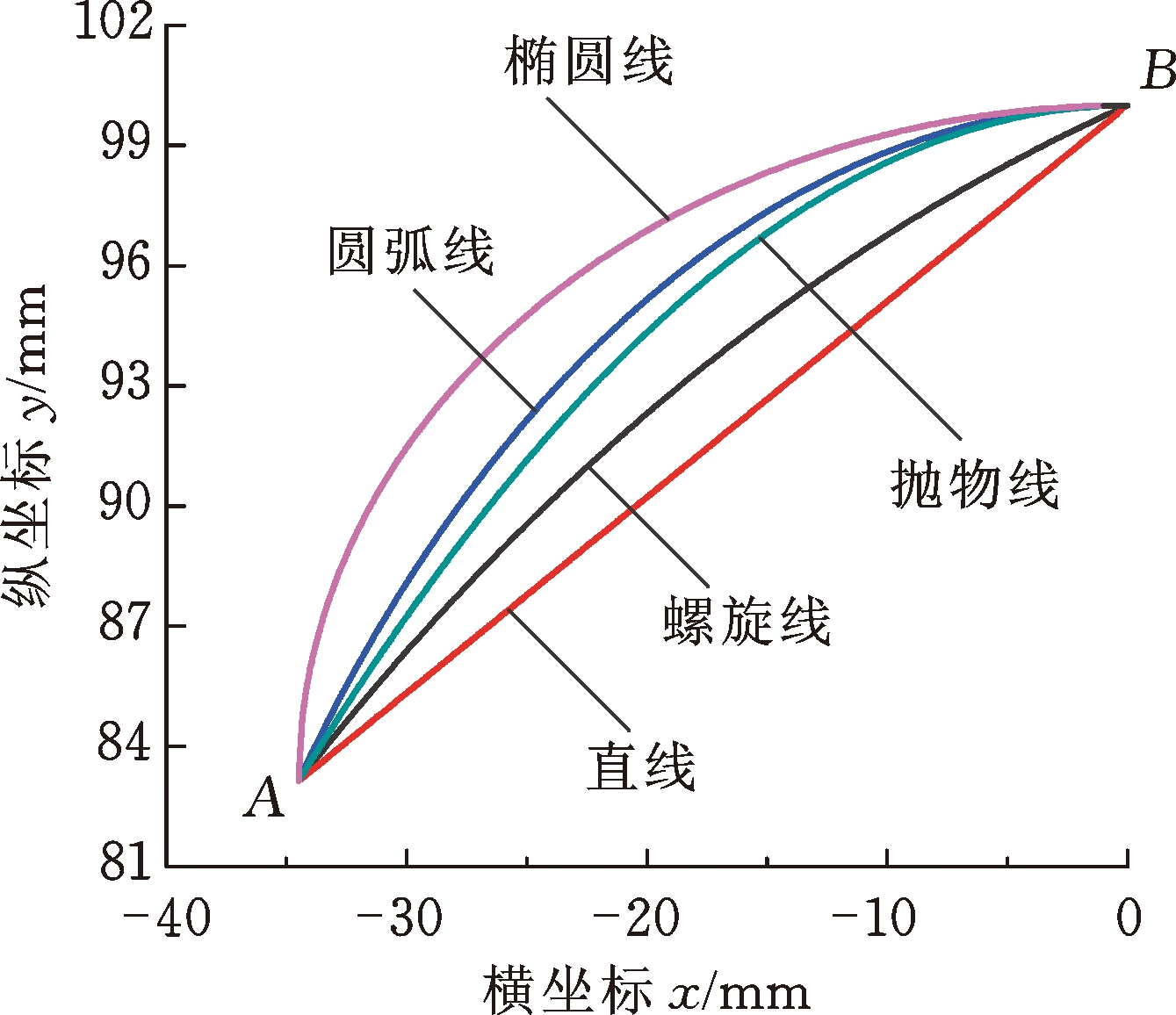
(a) 经典几何曲线
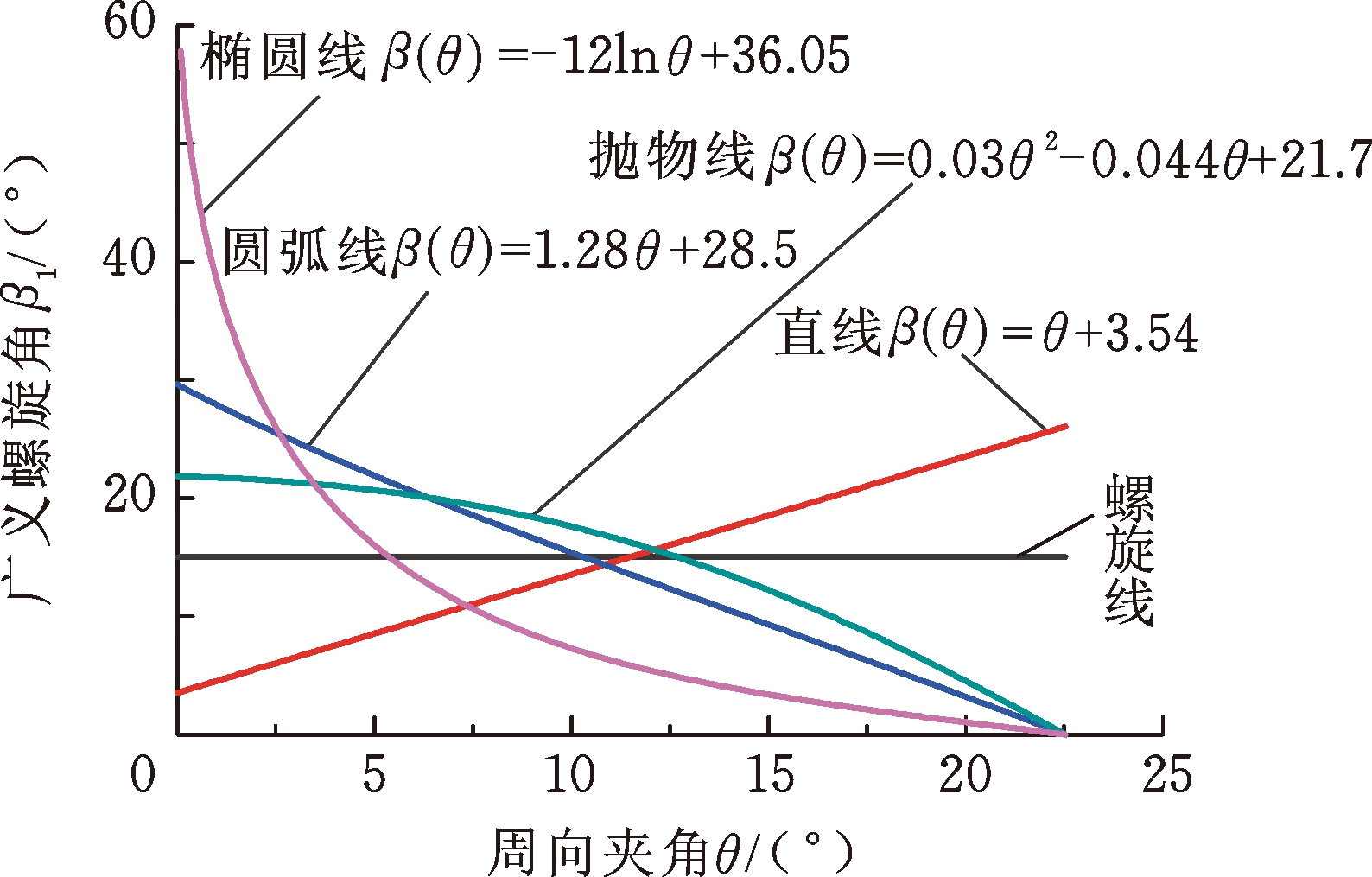
(b) 广义螺旋角
图3 经典几何曲线及其广义螺旋角分布
Fig.3 Typical geometrical curves and its corresponding generalized spiral angle distribution
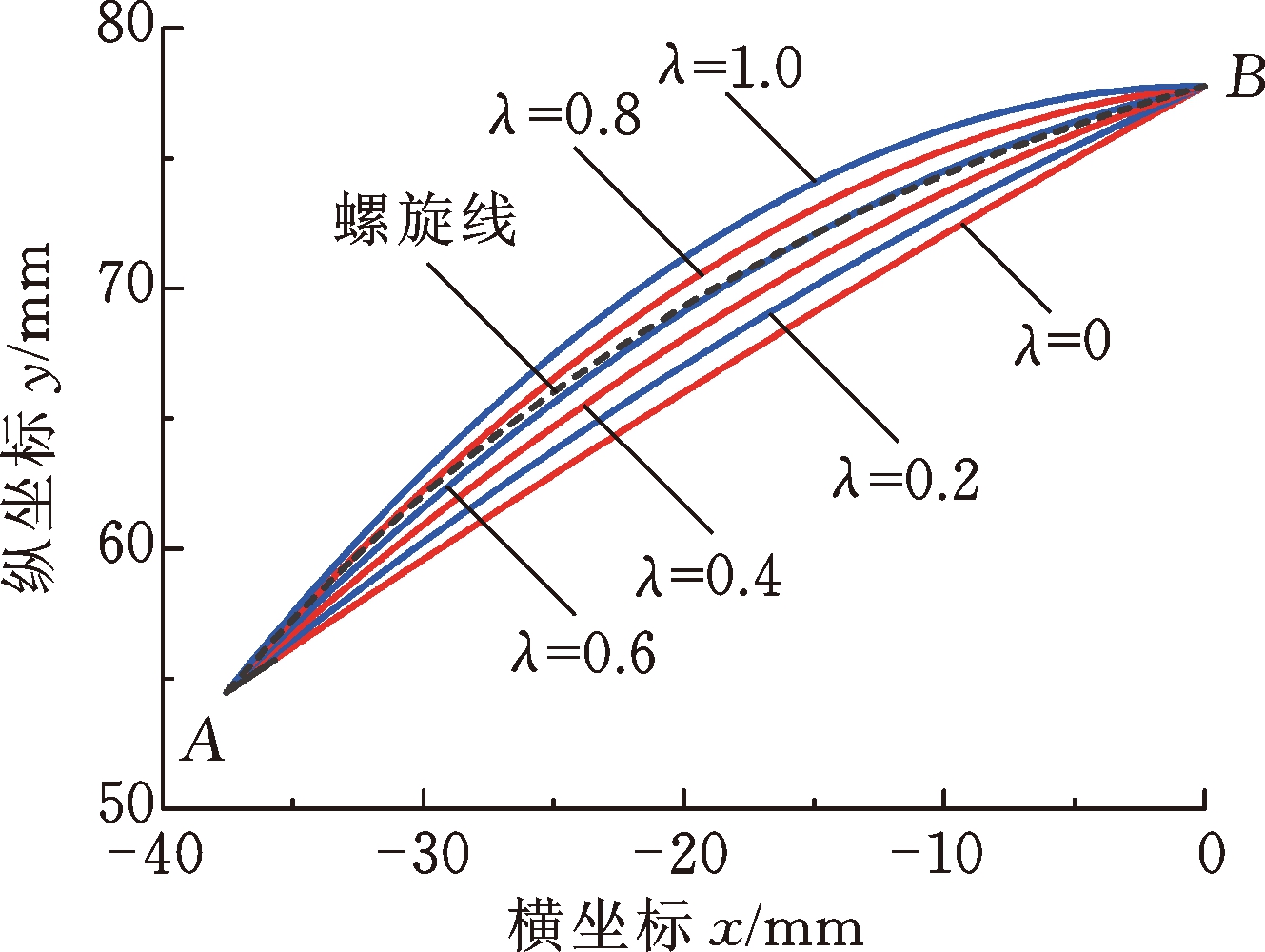
实际上,AB之间存在着无数条可能的圆弧线和抛物线,所有可能的圆弧线和抛物线都介于各自的内外边界型线之间,其中,内边界型线定义为槽根处的广义螺旋角最小时的型线,外边界型线定义为在外径处的广义螺旋角最小时的型线,定义量纲一参数λ为圆弧线和抛物线的型线位置系数,λ为0和1分别对应内外边界型线。图4所示为不同型线位置系数条件下的圆弧线和抛物线,可以看出,型线位置系数λ很小时,抛物线和圆弧线近似于直线;随着型线位置系数的增大,圆弧线和抛物线的特征越趋明显,与其他型线之间的差别也逐渐增大,故下文中选取λ=1的圆弧线和抛物线作为研究对象。
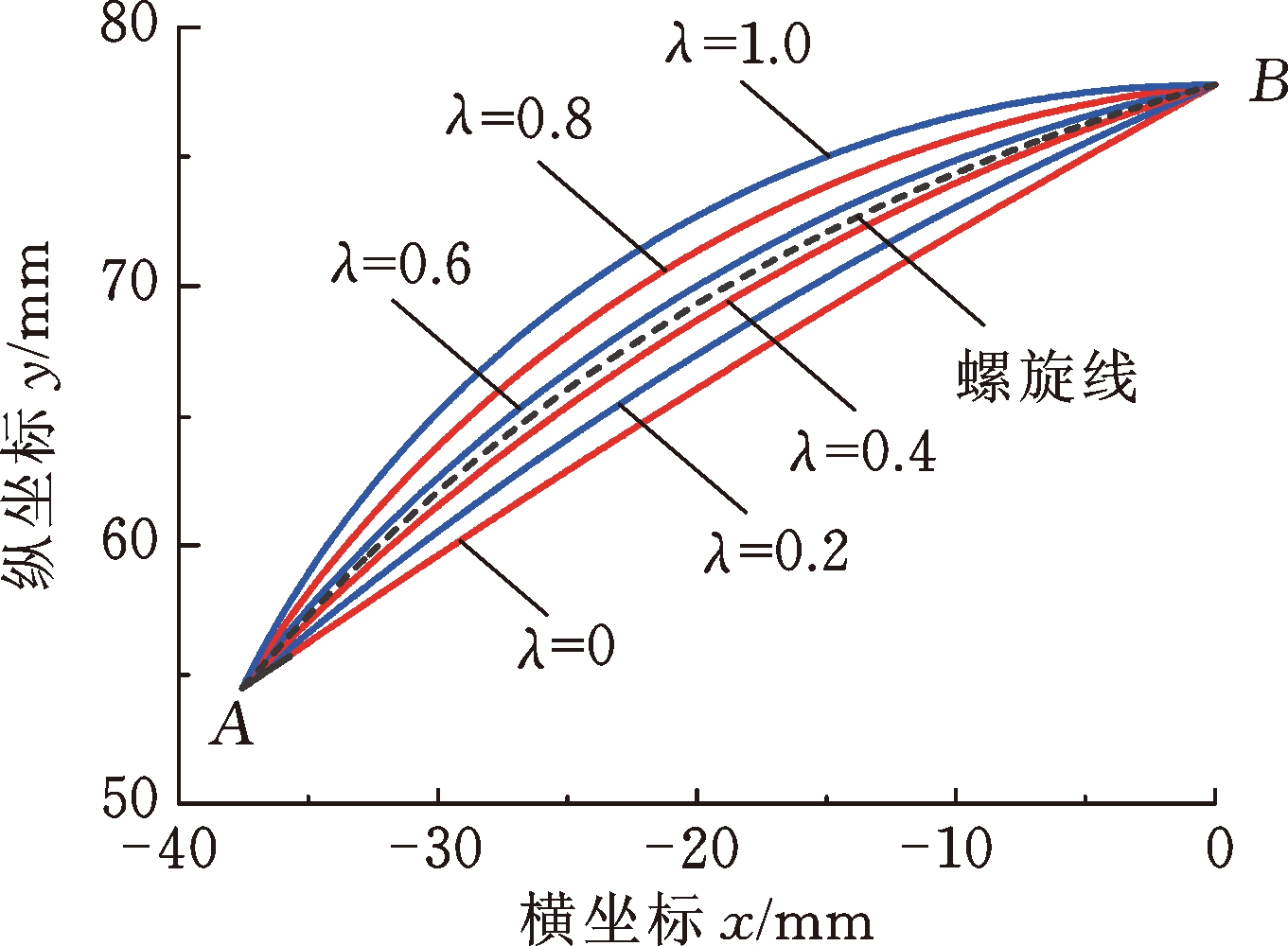
(a) 圆弧线
(b) 抛物线
图4 不同参数条件下的圆弧线和抛物线示意图
Fig.4 Schematic diagram of circular arc and parabola at different geometrical parameters
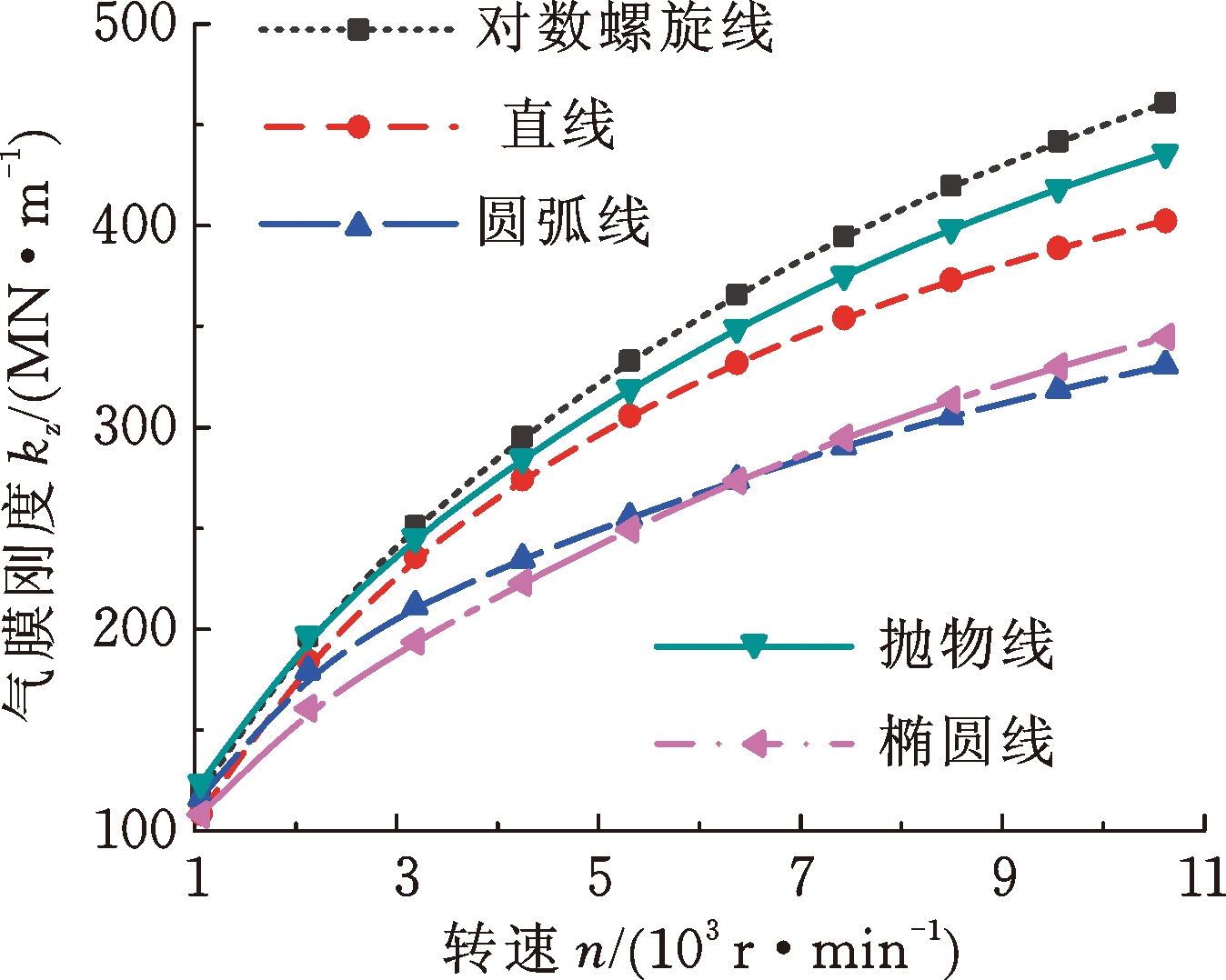
图5所示为几种经典几何型线推力轴承的承载力和气膜刚度随转速n的变化规律。由图5可知,随着转速的增大,承载力和气膜刚度都减速递增。高速条件下,经典对数螺旋槽推力轴承的承载力和气膜刚度最佳,抛物线型槽的次之,圆弧线型槽和椭圆线型槽的最差。这说明经典对数螺旋槽端面具有最佳的流体动压效应和气膜稳定性,这与文献[1]的结论是一致的。实际上,经典几何型线(圆弧线、直线和椭圆线等)的固有数学模型在方便描述型线的同时,也使得型线的表征能力变差,可优化的尺寸参数减少,将其作为型线的端面型槽往往难以产生很强的流体动静压效应。

(a) 承载力
(b) 气膜刚度
图5 转速对轴承承载力和气膜刚度的影响
Fig.5 Influence of rotating speed on load-carrying capacity and film stiffness of grooved bearing
2.2 广义螺旋角分布对轴承性能的影响
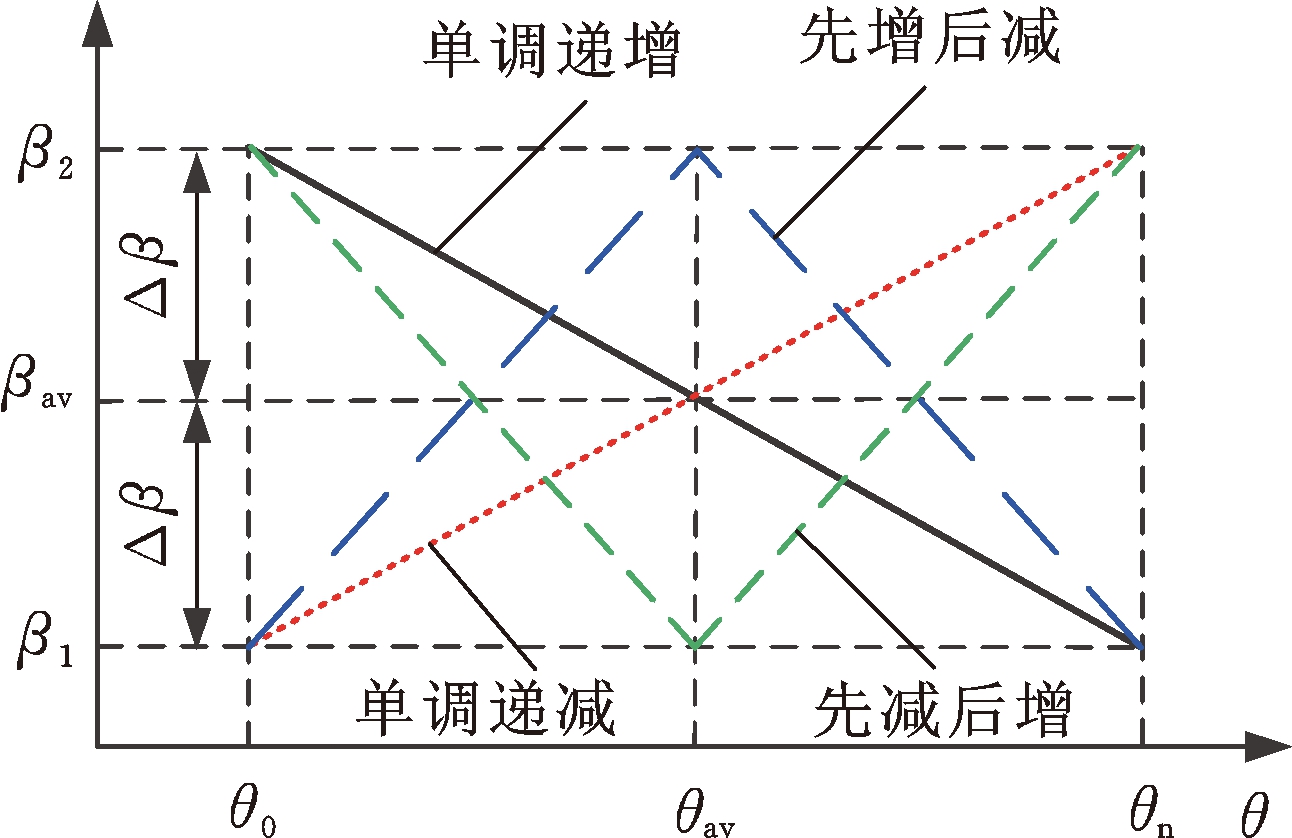
从上述经典型线的广义螺旋角分布可看出,一般型线的广义螺旋角并非定值,而是沿着周向呈现出一定规律的分布。图6所示为广义螺旋角β(θ)沿周向从θn(外径侧)至θ0(内径侧)的变化规律,其中,β1、β2、βav、Δβ分别为广义螺旋角的最小值、最大值、平均值和变化幅值,θ0、θn、θav分别为广义对数螺旋线的起始点、终止点和周向等分点的周向角度,图1b所示的广义对数螺旋线中,起始角度θ0=0,终止角度θn=α。
β(θ)=aθ+b时,式(5)可写成:
(9)
表2所示为4种典型β(θ)分布的系数a和b,其中,γ=εβav/(θ0-θn)。
(a)线性分布规律
(b)不同分布规律
图6 典型广义对数螺旋线的广义螺旋角分布
Fig.6 Generalized spiral angle distribution of typical generalized logarithm helix
表2 典型β(θ)分布对应的系数a和b
Tab.2 Coefficients a and b for typical distribution of β(θ)

β(θ)规律系数a系数b单调递增2γβav(1+ε)-2θ0γ单调递减-2γβav(1-ε)+2θ0γ先增后减a=-4γθ<θav4γθ≥θav b=βav(1-ε)+4θ0γθ<θavβav(1-ε)-4θnγθ≥θav 先减后增a=4γθ<θav-4γθ≥θav b=βav(1+ε)-4θ0γθ<θavβav(1+ε)+4θnγθ≥θav
图7所示为螺旋角变化幅值比ε不同时, 4种典型β(θ)分布的广义对数螺旋线及其对应的广义对数螺旋槽。从外径至内径侧,广义螺旋角单调递增时,广义对数螺旋线对应的型槽流道逐渐变宽,由其作为侧壁型线的广义对数螺旋槽为“流道渐扩槽”(图7a);广义螺旋角单调递减时,广义对数螺旋线对应的型槽流道逐渐变窄,由其作为侧壁型线的广义对数螺旋槽为“流道渐缩槽”(图7b);当广义螺旋角先减后增和先增后减时,由其作为侧壁型线的广义对数螺旋槽分别为“先缩后扩槽”(图7c)和“先扩后缩槽”(图7d)。螺旋角变化幅值比ε越大,广义对数螺旋线偏离经典对数螺旋线越远。由此可见,相较于直线、圆弧线和抛物线等经典几何型线,广义对数螺旋线具有更强的型线表征能力,通过改变螺旋角变化幅值比ε和平均广义螺旋角βav,可实现广义对数螺旋线向其他经典几何型线的转变。
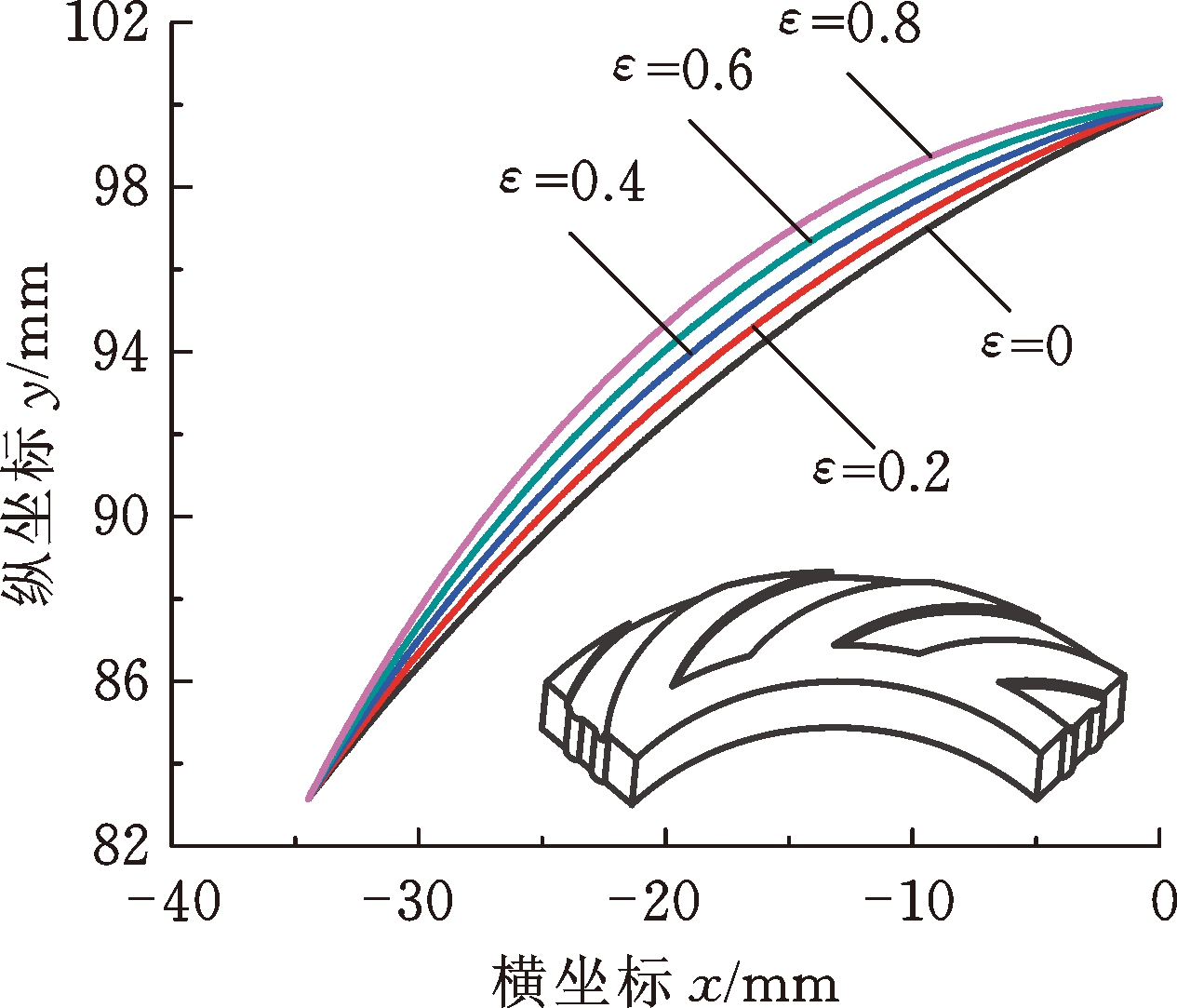
(a) 单调递增
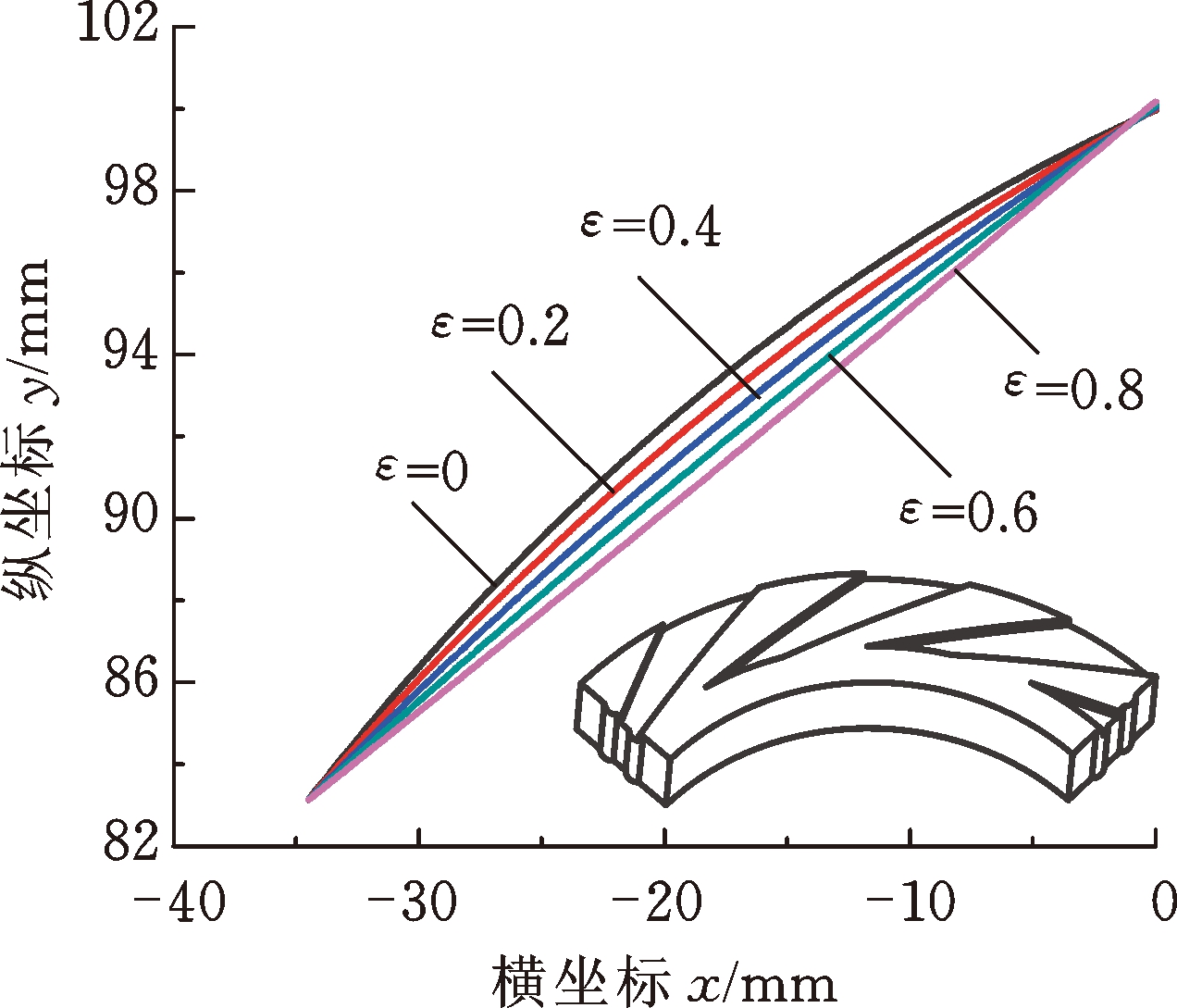
(b) 单调递减
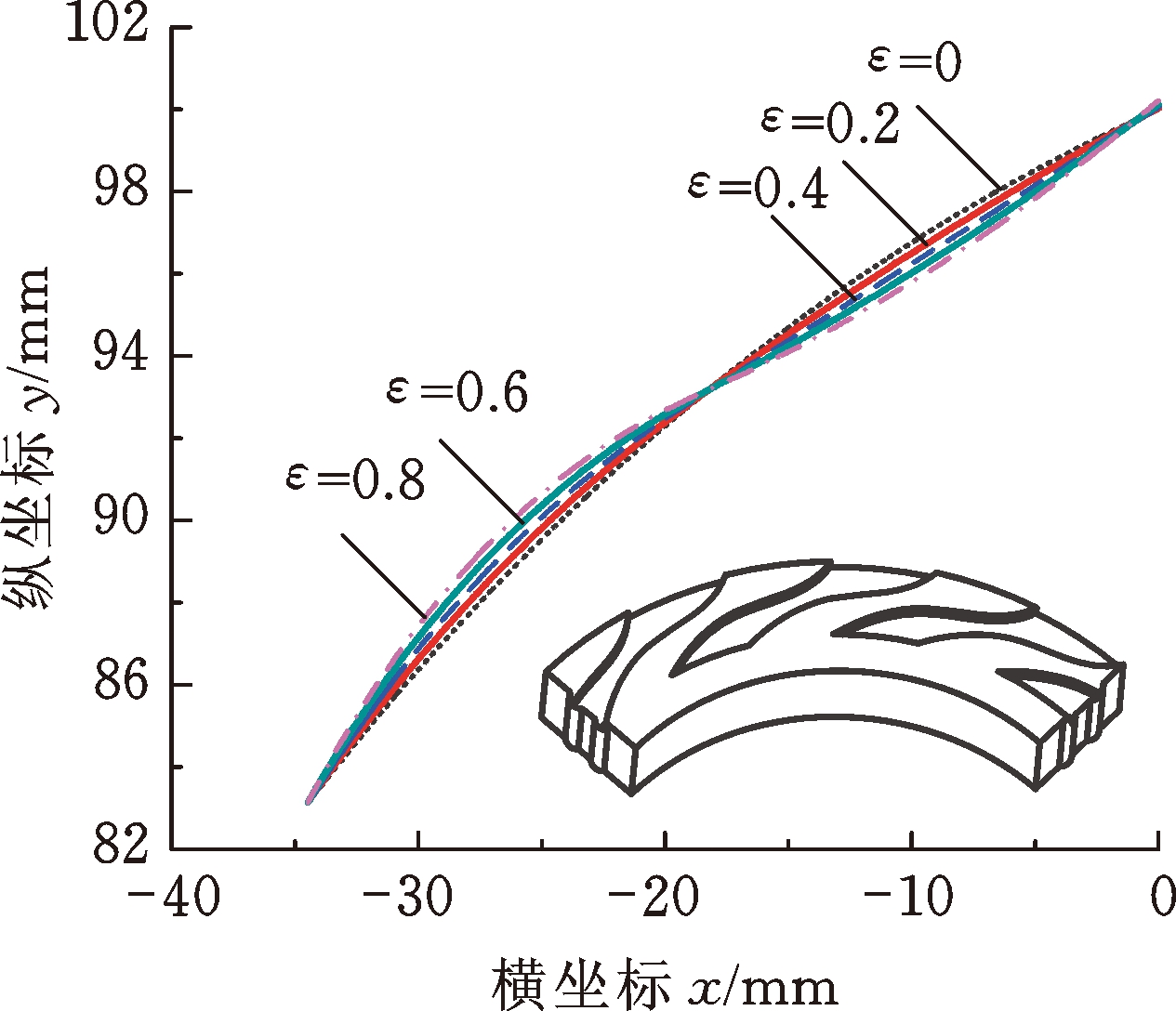
(c) 先减后增
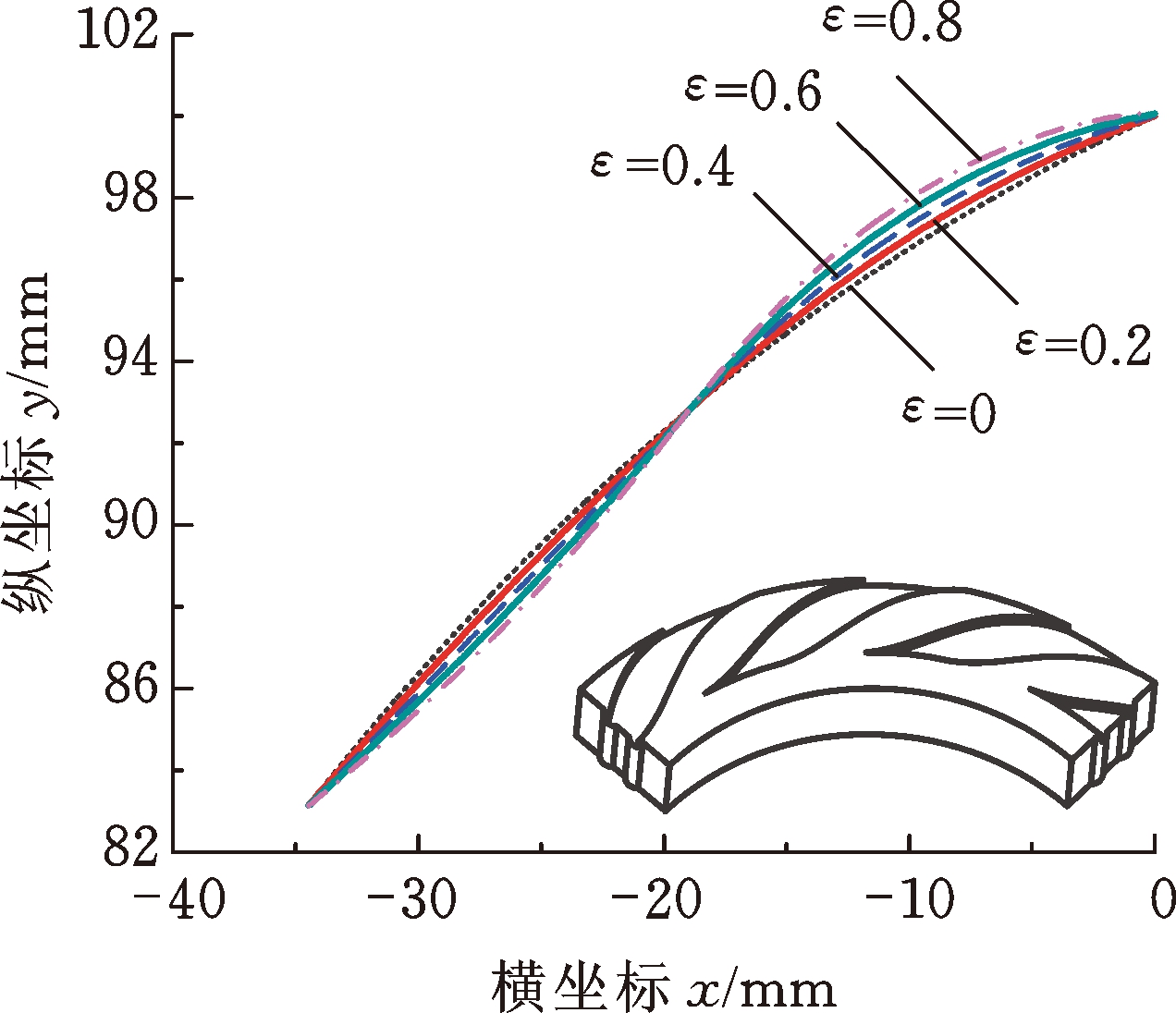
(d) 先增后减
图7 不同ε的4种典型广义对数螺旋线
Fig.7 4 typical generalized logarithm helixes at different ε
图8所示为4种典型螺旋角分布的广义对数螺旋槽推力轴承的承载力和气膜刚度随幅值比ε的变化规律,其中,ε=0对应经典对数螺旋槽。由图8可知,随ε的增大,流道渐扩槽(β(θ)单调递增)和先缩后扩槽(β(θ)先减后增)推力轴承的承载力和气膜刚度都先小幅增加、后迅速减小;流道渐缩槽(β(θ)单调递减)和先扩后缩槽(β(θ)先增后减)推力轴承的承载力和气膜刚度都迅速下降。从承载力来看,β(θ)沿周向非定值的广义对数螺旋槽与经典对数螺旋槽相比,并无明显优势;从气膜刚度来看,0.2≤ε≤0.4时的流道渐扩槽推力轴承相较于经典对数螺旋槽略有提高。
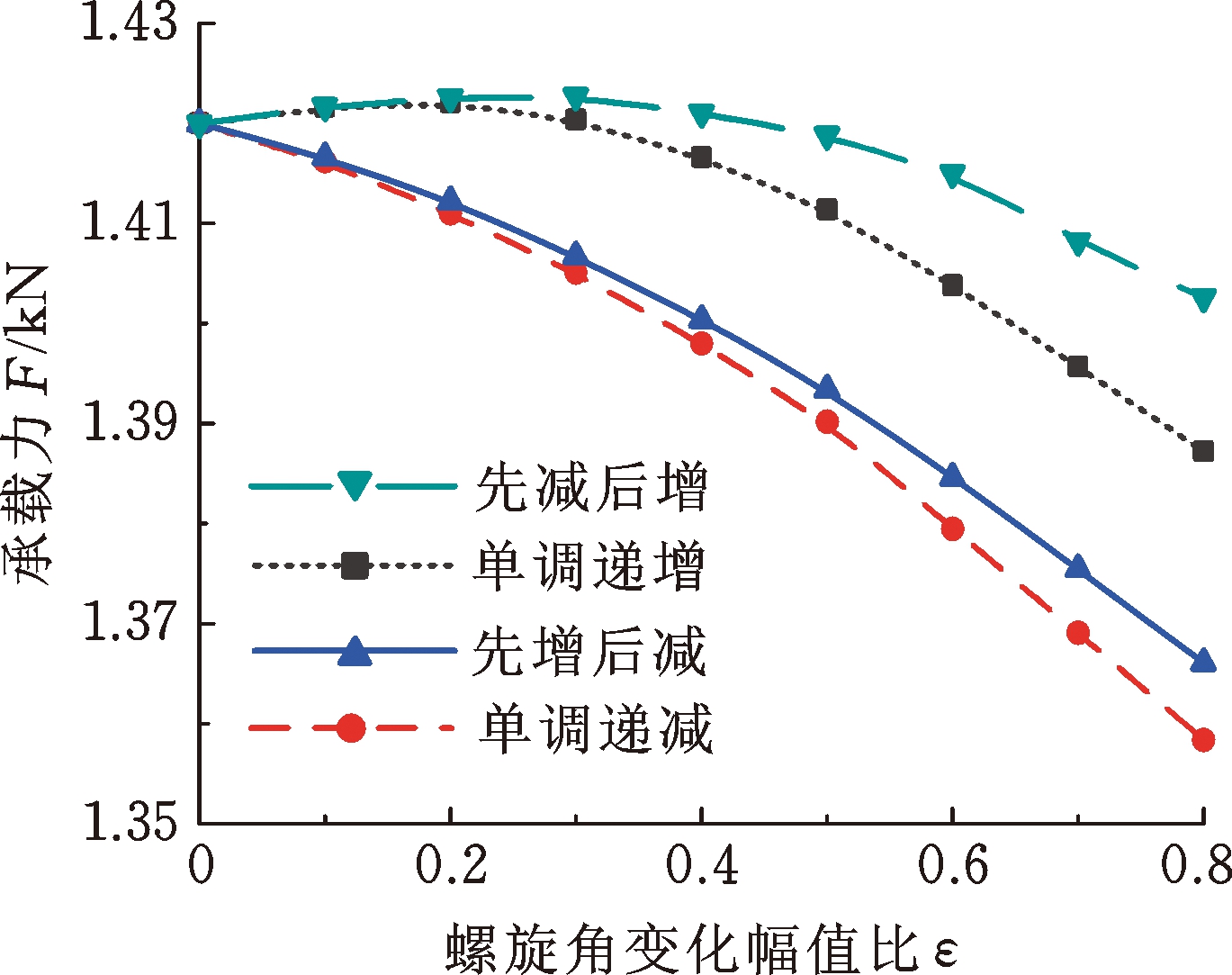
(a) 承载力

(b) 气膜刚度
图8 不同ε下螺旋角分布规律对承载力和刚度的影响
Fig.8 Influence of spiral angle distribution on load-carrying capacity and film stiffness at different values of ε
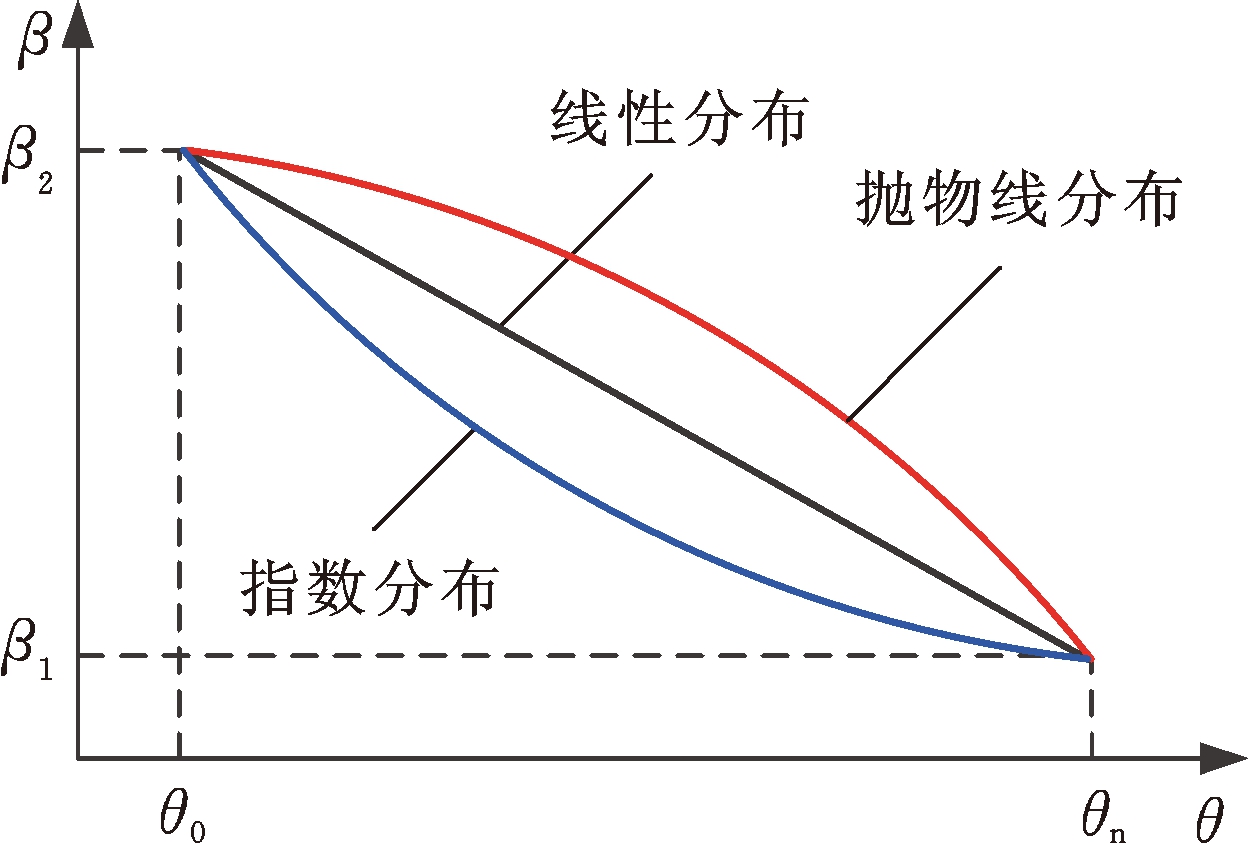
为进一步研究β(θ)为单调递增分布(流道渐扩槽)时,β(θ)对广义对数螺旋槽推力轴承性能的影响,对比分析了β(θ)分别为线性分布、抛物线分布和指数分布的广义对数螺旋槽与经典对数螺旋槽推力轴承的承载力和气膜刚度。由图9可看出,在靠近外径侧区域,3种不同β(θ)分布的广义对数螺旋线基本重合;在靠近起始半径处,指数分布的广义对数螺旋线在相同周向角度下的极径最大,线性分布次之,抛物线分布最小。

图9 典型螺旋角分布的广义对数螺旋线
Fig.9 Generalized logarithm helix with typical spiral angle distribution
图10所示为3种不同β(θ)分布下,广义对数螺旋槽推力轴承的承载力和气膜刚度随ε的变化规律。由图10可知,随着ε的增大,广义对数螺旋槽推力轴承的气膜刚度呈现出先增大、后减小的变化趋势,0.2≤ε≤0.5时获得最大值,不过增幅很小,这也说明广义螺旋角沿周向的递增或递减趋势一旦确定后,具体的变化规律(线性变化、抛物线变化抑或指数变化)对气体推力轴承的稳态性能影响较弱。指数分布的广义对数螺旋槽推力轴承气膜刚度最大,线性分布次之,抛物线分布最小。这是因为在高速条件下,周向剪切流占主导作用。β(θ)呈指数分布时,广义对数螺旋槽入口处较小的螺旋角有利于将密封腔内的气体介质泵入到密封端面之间,产生更强的流体动压效应。
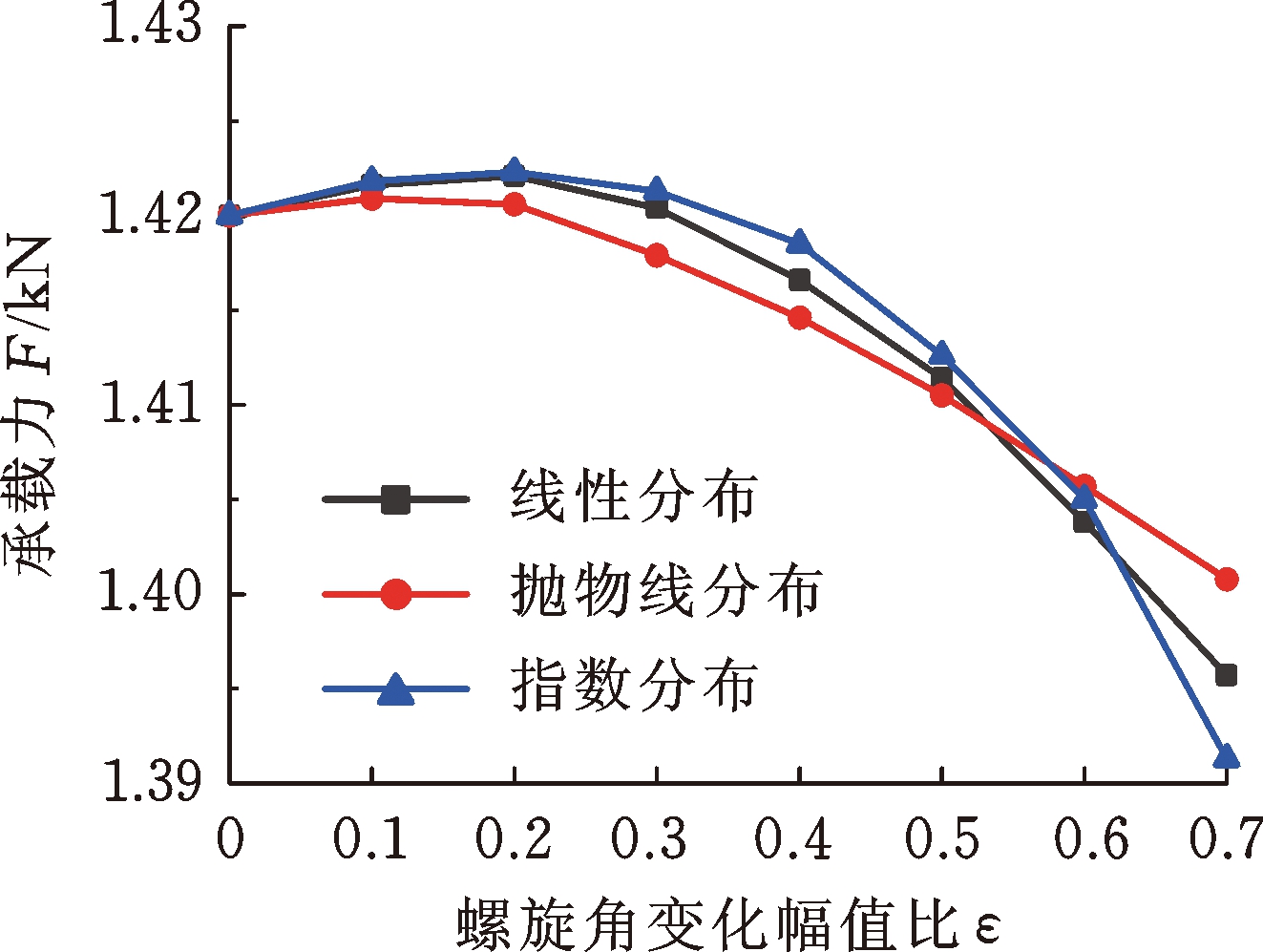
(a) 承载力
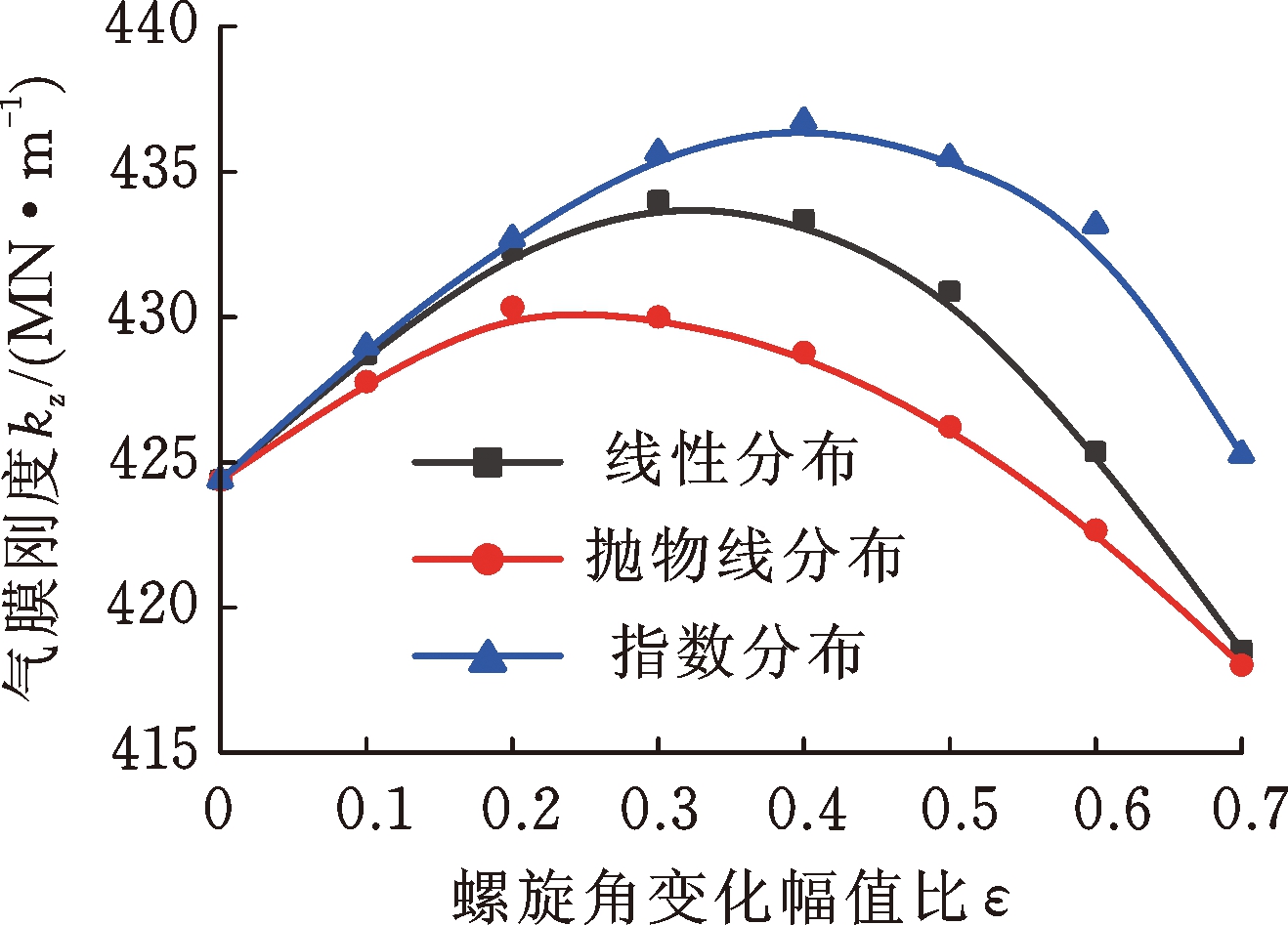
(b) 气膜刚度
图10 β(θ)分布规律对推力轴承承载力和气膜刚度的影响
Fig.10 Influence of β(θ) distribution on load-carrying capacity and film stiffness of thrust bearings
3 结论
(1)针对经典几何型线受其固定数学模型固有特性的限制,基于对数螺旋线方程,推导出广义对数螺旋线的极坐标方程,它相较于经典的直线、圆弧线、抛物线和椭圆线具有更强的几何表征能力。
(2)经典对数螺旋槽推力轴承的承载力和气膜刚度都优于将直线、圆弧线、椭圆线和抛物线作为侧壁型线的广义对数螺旋槽推力轴承,对数螺旋槽是一种能产生较强流体动压效应的端面结构。
(3)在高速条件下,相较于对数螺旋槽推力轴承,从外径至内径型槽流道渐扩的广义对数螺旋槽推力轴承具有更大的气膜刚度,其中,以广义螺旋角呈指数递增分布为最佳。
[1] GABRIEL R P. Fundamental of Spiral Groove Non-contacting Face Seals[J]. Lubrication Engineering, 1994, 50(3): 215-224.
[2] SALANT R F, HOMILLER S J. The Effects of Shallow Groove Patterns on Mechanical Seal Leakage[J]. Tribology Transactions, 1992, 35(1): 142-148.
[3] LIU X Y, LIU X W. Influence of Groove Molded Lines on the Lubrication Performance of Water-lubricated Spiral Groove Thrust Bearings[J]. Advanced Materials Research, 2013, 694/697: 538-542.
[4] 吴宗祥, 郝木明, 顾永泉. 低速干气端面机械密封性能研究[J]. 流体机械, 1994, 22(6): 7-11.
WU Zongxiang, HAO Muming, GU Yongquan. Performance Research of Dry Gas Seal at Low Speed[J]. Fluid Machinery, 1994, 22(6): 7-11.
[5] CHEN Y, JIANG J B, PENG X D. Dynamic Characteristics and Transient Sealing Performance Analysis of Hyperelliptic Curve Groove Dry Gas Seals[J]. Tribology International, 2017, 116: 217-228.
[6] 胡丹梅, 吴宗祥. 直线槽端面气体密封分析计算[J]. 流体机械, 1996, 24(9): 16-22.
HU Danmei, WU Zongxiang. Performance Analysis of Oblique Groove Gas Face Seal[J]. Fluid Machinery, 1996, 24(9): 16-22.
[7] HASHIMOTO H. Optimization of Groove Geometry for a Thrust Air Bearing According to Various Objective Functions[J]. ASME Journal of Tribology, 2008, 131(4): 327-329.
[8] SHEN C, KHONSARI M M. Numerical Optimization of Texture Shape for Parallel Surfaces under Unidirectional and Bidirectional Sliding[J]. Tribology International, 2015, 82: 1-11.
[9] 魏超, 陈国明, 栾智存, 等. 车用旋转密封件动压槽型线优化研究[J]. 北京理工大学学报, 2016, 36(1): 25-30.
WEI Chao, CHEN Guoming, LUAN Zhicun, et al. Optimization on the Hydrodynamic Groove Geometry of Rotary Seals for Automotive Transmissions[J]. Transactions of Beijing Institute of Technology, 2016, 36(1): 25-30.
[10] 许鹏先, 潘琦, 申改章, 等. 一种干气密封槽型的设计方法[J]. 润滑与密封, 2006(12): 177-179.
XU Pengxian, PAN Qi, SHEN Gaizhang, et al. A Design Method of Dry Gas Seal Groove[J]. Lubrication Engineering, 2006(12): 177-179.
[11] 丁雪兴, 赵芳, 黄义仿, 等. 拟合曲线槽干气密封流场的数值模拟及分析[J]. 润滑与密封, 2013, 38(2): 35-38.
DING Xuexing, ZHAO Fang, HUANG Yifang, et al. Numerical Simulation and Analysis of Flow Field for Dry Gas Seal with Fitted Curved Groove Based on Tracing Line [J]. Lubrication Engineering, 2013, 38(2): 35-38.
