0 引言
轴向力作用在产生挠曲的构件或竖直载荷作用在产生侧移的结构上引起的附加作用效应称作二阶效应,也称为轴力效应。结构或构件中的附加内力和附加变形是由几何非线性产生的二阶效应,因此二阶效应分析方法是解决几何非线性问题的一种方法,属于几何非线性方法之一。工程中有一大类结构在承载后有相对明显的变形,如履带起重机的桁架臂这种细长桁架结构,其横截面积较小,柔度较大,存在刚性不足的问题,在自重载荷下会出现较大的初始下挠变形,当受到轴向载荷和横向载荷共同作用后,易出现结构的“软化”现象,因此不能忽略这种几何非线性对结构受力和变形的影响。本文从结构二阶效应入手,分析研究结构的几何非线性方法。
结构二阶效应的常见分析方法有有限元法和微分方程法。目前有限元法的理论研究已经取得了丰富的成果[1]。SCHARPF[2]运用矩阵位移法求解结构应力。BIRNSTIE等[3]运用Hermite插值研究梁单元的二阶效应,但需要用3个或4个单元才能拟合一根杆件,取得较好的精度。TO[4]用三次多项式来研究梁的挠度,推导梁的刚度矩阵。LI等[5]通过运用Chebyshev多项式方法得到Timoshenko-Euler楔形梁的单元刚度矩阵。谢贻权等[6]推导了梁单元的切向刚度矩阵,并求出了其显式表达式。陆念力等[7]运用普通的非线性有限元结合随动坐标法,推导了大位移杆系结构的一般非线性的全量平衡方程和增量平衡。采用有限元法理论上可获得高精度的全量与增量平衡方程和各刚度矩阵,但单元刚度矩阵由插值理论推导所得,且为显式表达刚度矩阵,会省略某些高阶非线性项,这两者均会导致实际中最终梁杆有限元方程精度的下降。
本文基于二阶效应,首先在变形后的位置上建立承受横向均布载荷压杆的弯曲平衡方程,然后将挠曲线方程变换成以待定的几何参数表达的普遍形式[8],再根据特定的边界条件和平衡条件求解待定几何参数,得到挠曲变形方程。最后,采用该方法分析求解存在二阶效应的履带起重机桁架臂标准节模型的挠度变形,并与常用有限元软件ANSYS和ABAQUS几何非线性的计算结果进行对比。
1 承受横向均布载荷的压杆弯曲问题的求解方法
1.1 压杆弯曲的微分方程及其解
一承受横向均布载荷q的等截面受压杆力学模型见图1,杆件长度为L,杆件两端有轴向压力P、横向剪力Q以及弯矩M的作用,以杆变形前的轴线为x轴,侧向挠曲变形方向为y轴建立坐标系,则杆变形后的挠曲微分方程为
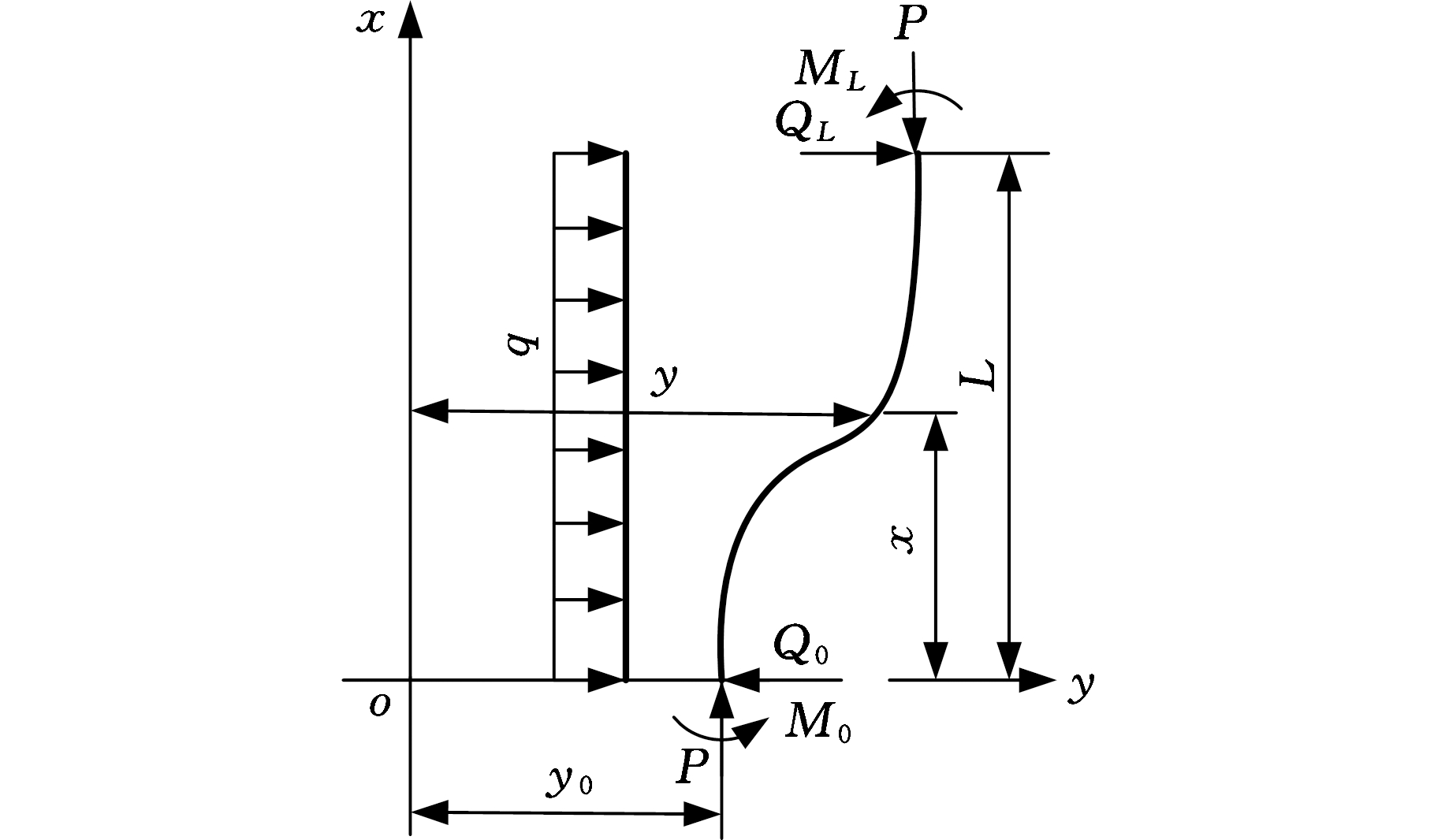
图1 压杆受力简图
Fig.1 Compression rod force diagram
![]()
(1)
式中,E为弹性模量;I为截面惯性矩。
令k2=P/EI,则式(1)可写成:
(2)
则微分方程式(2)的通解为
y=A1coskx+A2sinkx+A3x2+A4x+A5
(3)
式中,Ai(i=1,2,…,5)为待定的积分常数,可由边界条件求出。
引入参数φ和系数A,令
(4)
(5)
将式(4)、式(5)代入式(3),可得
y=Asin(kx-φ)+A3x2+A4x+A5
(6)
引入参数μ,μ为压杆有效长度系数,μL即为正弦曲线的两个反弯点之间的距离,两个反弯点之间的杆段是一个典型的二力杆的欧拉弯曲模型,则
(7)
将式(7)代入k的表达式,则
(8)
压杆截面的弯矩
M=PAsin(kx-φ)
(9)
引入参数ζ,ζ为反弯点系数,ζL表示x轴正方向第一个反弯点到坐标原点的距离,在反弯点处,x=ζL,M=0,代入式(9),则
(10)
将式(8)、式(10)代入式(6),则用几何参数表达的压杆挠曲方程为
y=Asin((x/μL-ζ/μ)π)+A3x2+A4x+A5
(11)
式(11)为挠曲线微分方程式(1)的通解,适用于任意边界条件的压杆。对于给定边界条件的压杆,求其特解的问题可转化为根据杆端的变形连续条件和力的平衡条件确定挠曲线方程的几何参数问题。
1.2 压杆弯曲变形挠曲线的分解
由式(11)可知,挠曲微分方程由正弦曲线Asin((x/(μL)-ζ/μ)π)和抛物线A3x2+A4x+A5两部分组成,由于考虑了二阶非线性,故简单的叠加不适用于此处的非线性求解方法。若上述两变形曲线均承受轴向压力的作用,则可以将两者变形叠加[9]。杆的受力分解叠加原理示意简图见图2。挠曲线分解为两部分:在任意截面上只承受轴向压力P和弯矩Mx的正弦曲线;承受横向载荷、杆端横向剪力和轴向压力P作用的二次抛物线,杆处于轴心受压的曲线平衡状态。
1.3 待定系数的确定
根据边界条件和平衡条件求解二次抛物线的系数A3和A4,二次抛物线可表示为
yi=A3x2+A4x+A5
(12)
抛物线转角θi的方程为
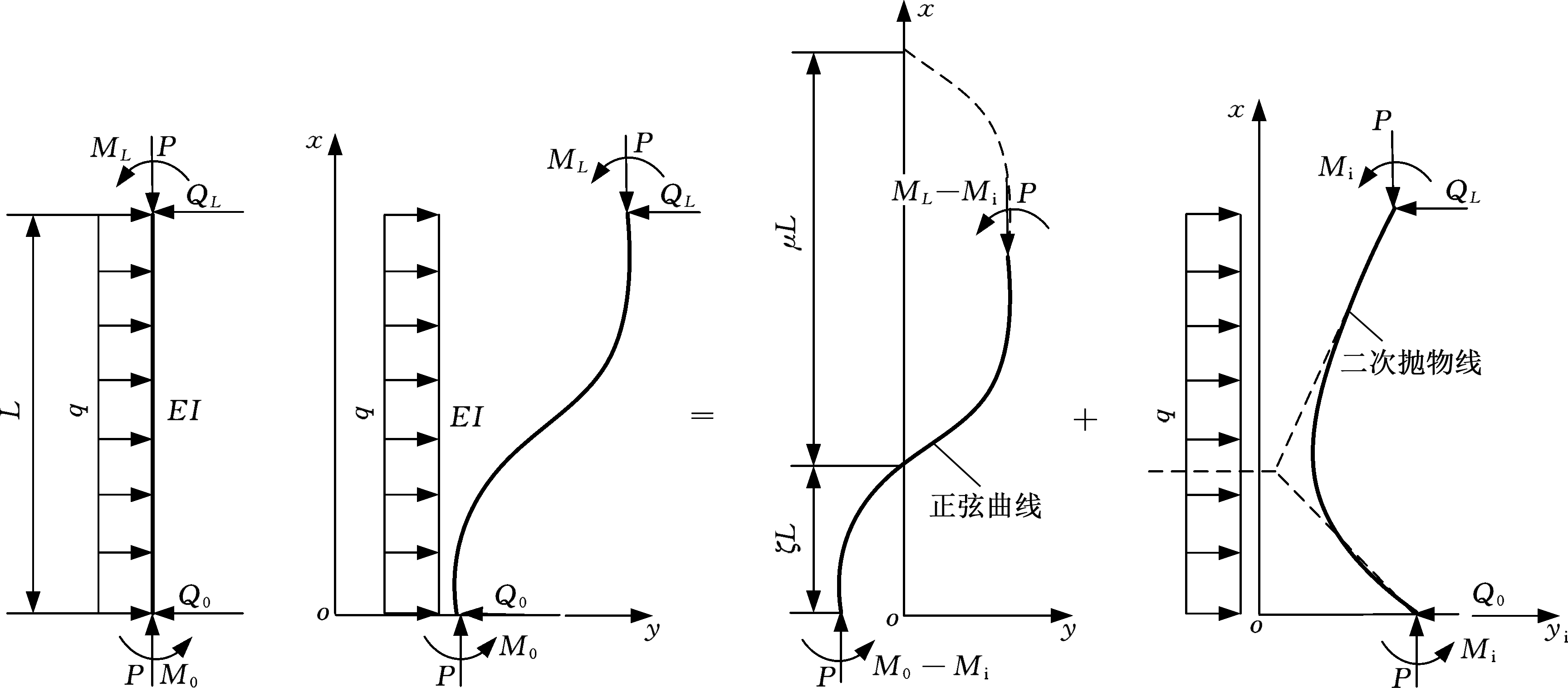
(a) (b)
图2 压杆受力分解叠加原理示意简图
Fig.2 Schematic diagram of force decomposition and superposition principle of pressure bar tanθi=2A3x+A4
(13)
在杆端x=0处,抛物线的斜率等于轴向力P和杆端水平反力Q0的合力作用线与x轴的夹角的正切值,即
(14)
同理,在x=L处有:
(15)
又y方向力的代数和为零,有qL=QL-Q0,代入式(15),可得
(16)
则抛物线可表示为
(17)
杆的弯曲变形为
(18)
式(18)中的A、ζ、A5均可由边界条件和平衡条件求出,压杆的转角方程和截面上弯矩方程分别为
(19)
(20)
2 承受横向均布载荷的悬臂压杆公式求解
承受横向均布载荷的等截面悬臂压杆受力分解叠加原理示意图见图3,由式(18)~式(20)即可求出系数A、ζ、A5。
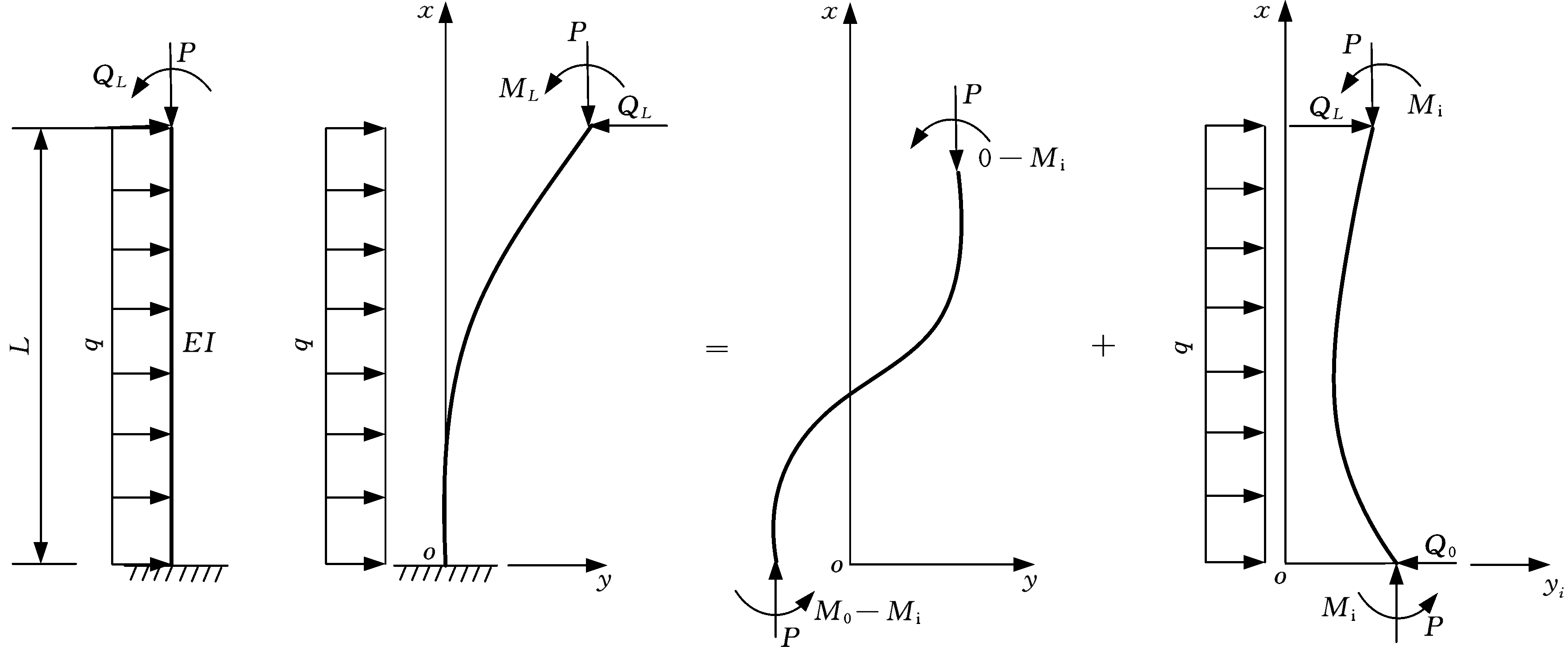
(a) (b)
图3 横向均布载荷悬臂压杆受力分解叠加原理示意简图
Fig.3 Schematic diagram of force decomposition and superposition principle of cantilever pressure bar under transverse uniform load
杆固定端转角等于零,可得x=0,θ0=0,代入式(19),得
(21)
杆自由端弯矩等于零,可得x=L,ML=0,代入式(20),得
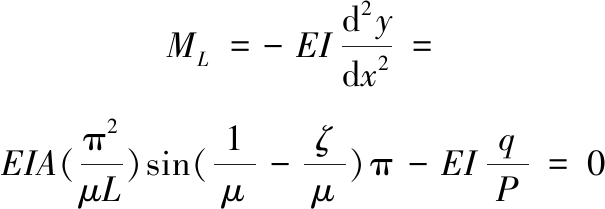
(22)
联立式(21)、式(22),整理得
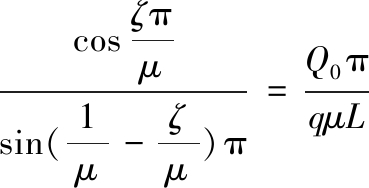
(23)
解得
式中,μ由式(7)确定。
求出ζ后,将ζ代入式(21)中,可得
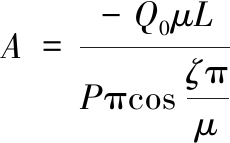
将边界条件x=0、y=0代入式(18),可得
则压杆挠曲线方程为
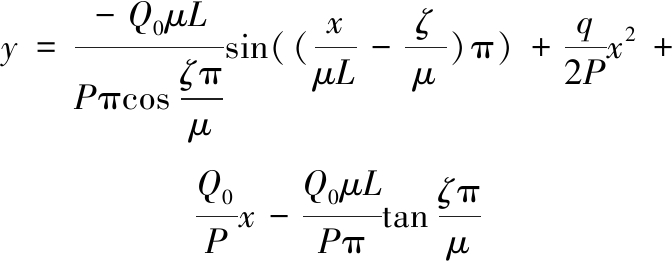
(24)
令x=L,则压杆顶端挠度为
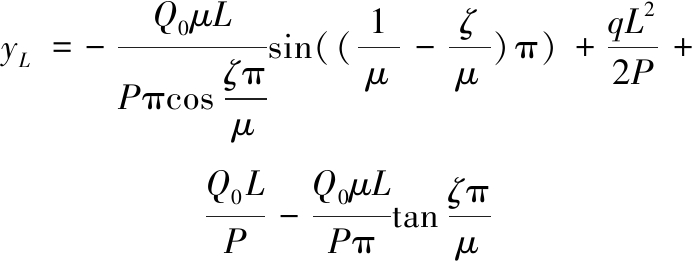
(25)
3 算例分析
使用本文所提出的方法,对280t级履带起重机桁架臂标准节模型进行分析,求解其挠度变形,并与ANSYS和ABAQUS两种有限元软件非线性分析计算结果进行对比。
履带起重机空间桁架臂标准节模型实际结构见图4,由外径159 mm、内径139 mm的弦杆和外径76 mm、内径67 mm腹杆焊接而成,长度为L,桁架臂左端为固定端,悬臂自由端承受轴向压力P和横向力Q0,图5为桁架臂的等效模型,IL为将上述履带起重机不同长度的格构式空间桁架臂等效为实腹式结构后的等效惯性矩[10],q为臂架自重均布载荷。在通用有限元软件ANSYS中运用BEAM188单元分别建立不同长度的如图6a所示的履带起重机桁架臂的真实结构模型,在臂节其中一端施加全约束,对不同长度臂架施加相同大小的轴向压力P和横向力Q0,且均施加于与周围四肢节点形成刚性区域的节点之上,同理,在有限元软件ABAQUS中建立图6b所示臂架真实结构模型,约束与载荷施加方式方法与ANSYS模型相同,然后分别在ANSYS和ABAQUS中对不同长度的起重机臂架模型进行非线性分析,不同长度臂架的ANSYS和ABAQUS非线性分析的结果与本文计算结果如表1所示,其中y为悬臂端的挠度变形大小。
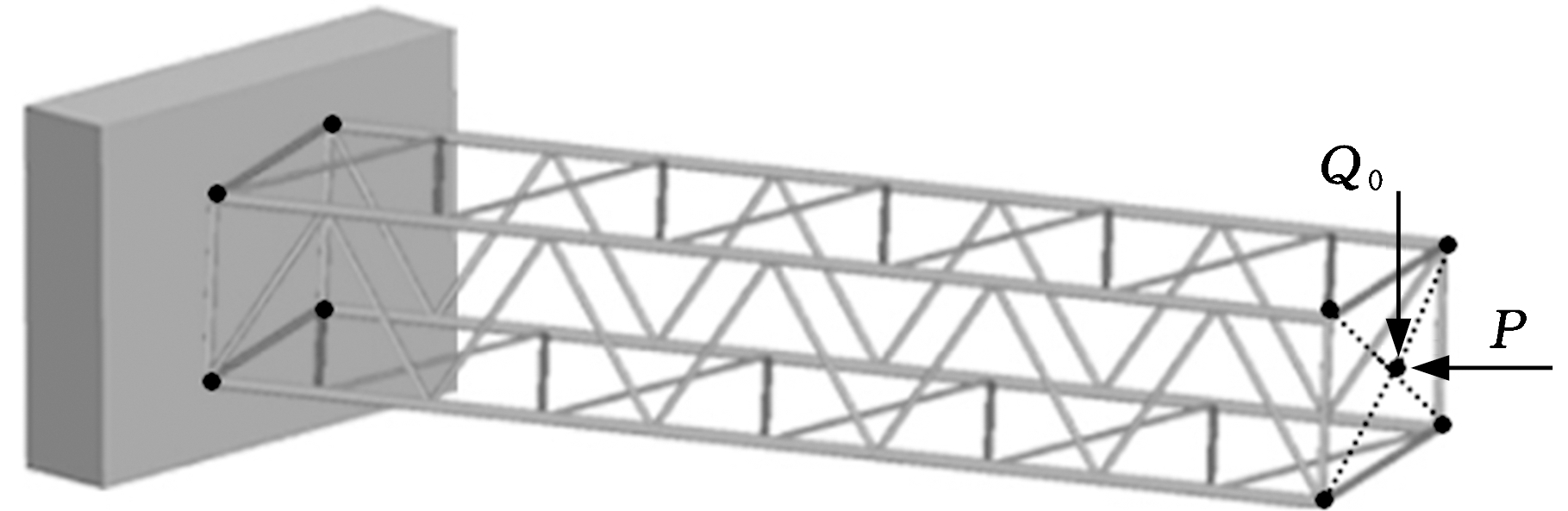
图4 履带起重机桁架臂标准节模型
Fig.4 Standard section model of trussed boom of crawler crane
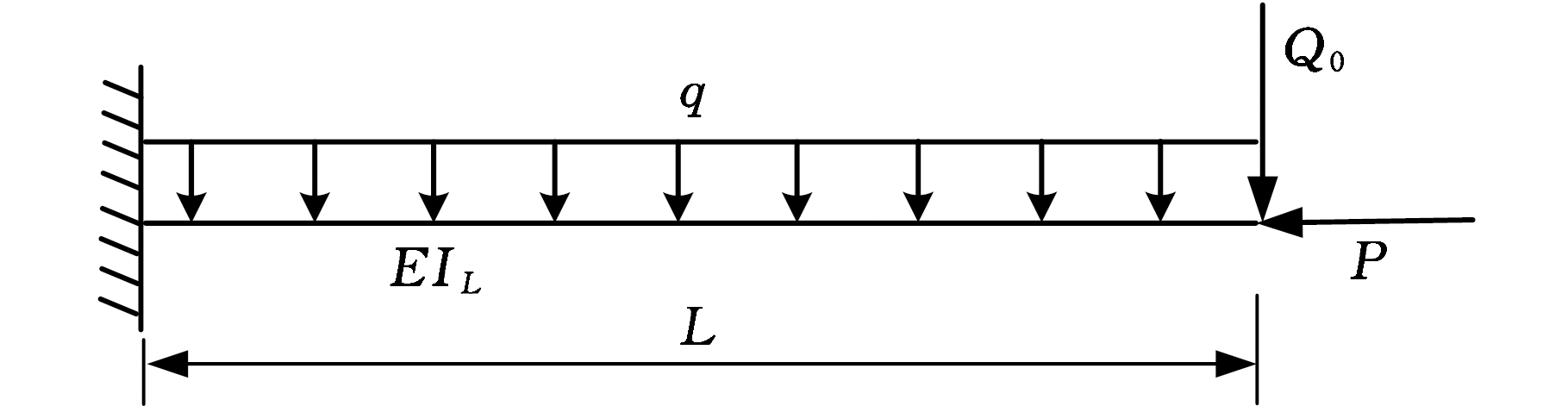
图5 起重机臂架等效悬臂梁模型
Fig.5 Equivalent cantilever beam model of the crane boom

(a)ANSYS模型 (b)ABAQUS模型
图6 有限元模型
Fig.6 Finite element model
表1 不同长度臂架的计算变形
Tab.1 Calculation of different lengths of boom deformation
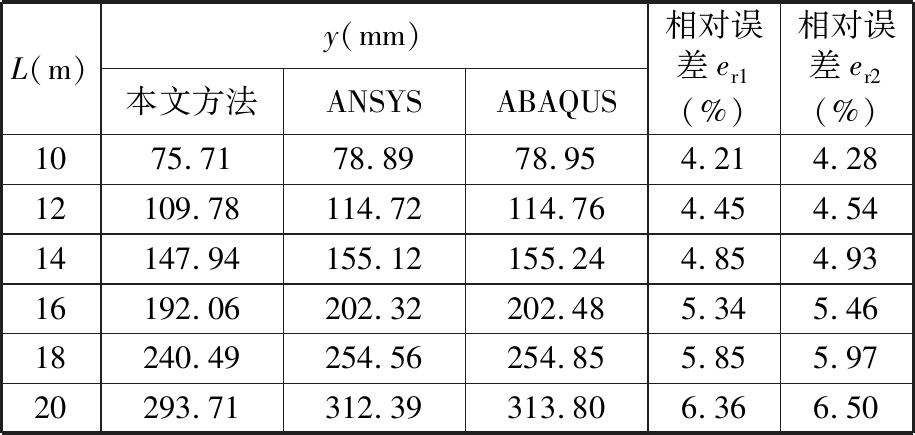
L(m)y(mm)本文方法ANSYSABAQUS相对误差er1(%)相对误差er2(%)1075.7178.8978.954.214.2812109.78114.72114.764.454.5414147.94155.12155.244.854.9316192.06202.32202.485.345.4618240.49254.56254.855.855.9720293.71312.39313.806.366.50
注:![]() 其中yM、yANSYS、yABAQUS分别为本文计算结果、ANSYS计算结果、ABAQUS计算结果。
其中yM、yANSYS、yABAQUS分别为本文计算结果、ANSYS计算结果、ABAQUS计算结果。
从计算结果可以看出,本文计算所得的挠度变形与ANSYS、ABAQUS软件非线性分析计算结果吻合程度较好,说明本方法是可信和有效的,可用来分析桁架臂的挠度变形,具有实用性;计算结果误差随着臂架长度的增大而有所增加,主要原因是随着L的增大,臂架的几何非线性越来越明显,臂架的等效惯性矩转化还存在一定的局限性,这是本文需要进一步深入研究和改进的工作。
4 结语
根据几何非线性引起的二阶效应的特点,建立压杆在变形位置后的挠曲微分方程,将微分方程变换成以待定的几何参数表达的普遍形式,求得承受横向均布载荷的悬臂压杆的变形方程,分析计算了存在二阶效应的起重机空间桁架臂标准节的挠曲变形,对比计算结果表明了本文方法的可行性与实用性。
[1] 王勖成.有限单元法[M].北京:清华大学出版社,2003.
WANG Xucheng. Finite Element Method[M]. Beijing: Tsinghua University Press, 2003.
[2] SCHARPF D W. New Method of Stress Calculation in the Matrix Displacement Analysis[J]. Computers and Structures, 1987, 8(3/4): 465-477.
[3] BIRNSTIE L C, IFFLAND J B. Factors Fluencing Frame Stability[J]. Journal of the Structural Division, 1980, 106(2): 491-504.
[4] TO C W S. Linearly Tapered Beam Finite Element Incorporating Shear Deformation and Rotary Inertia for Vibration Analysis[J]. Journal of Sound and Vibration. 1981, 78(4): 475-484.
[5] LI G Q, LI J J. A Tapered Timoshenko-Euler Beam Element for Analysis of Steel Portal Frames[J]. Journal of Constructional Steel Research, 2002, 58(12): 1531-1544.
[6] 谢贻权,何福保.弹性和塑性力学中的有限单元法[M].北京:机械工业出版社,1981.
XIE Yiquan, HE Fubao. Finite Element Mechinery[M]. Beijing: Industry Press,1981.
[7] 陆念力,孟丽霞.基于二阶理论的弹性约束变截面悬臂梁刚度与稳定性分析[J].工程力学,2012,29(12):365-369.
LU Nianli, MENG Lixia. Stiffness and Stability Analysis of Variable Cross-section Cantilever Beams Based on Second-order Theory [J]. Engineering Mechanics, 2012, 29 (12): 365-369.
[8] 刘晚成.压杆非线性问题的解析方法[M].哈尔滨:东北林业大学出版社,2002.
LIU Wancheng. Analysis Method of the Non-linearity of Compression Rod [M].Harbin: Northeast Forestry University Press, 2002.
[9] GEORGE J S. An Introduction to the Elastic Stability of Structures [M]. Englewood Cliffs and New Jersey: Prentice-Hall, Inc., 1976: 77-81.
[10] 安亭铮.履带起重机臂架系统回转平面稳定性研究[D]. 大连:大连理工大学,2015.
AN Tingzheng. Research on Stability of Swing Plane of Crawler Crane Boom System [D]. Dalian: Dalian University of Technology,2015.
