0 引言
由于存在物理试验成本和客观条件等限制，计算机仿真建模和分析已逐渐应用于设计及评估航空航天、机械等领域的复杂系统。高精度的数值模型是开展有效仿真分析的基础， 满足使用要求的数值模型才可用于仿真分析。工程实际中，普遍存在概率与区间混合不确定性情况[1-2]，有些模型参数可获得充足样本数据来构建精确的概率分布；而有些模型参数试验成本高及难度大，难 以获得足够样本数据来精确描述，只能估计其变化区间。虽然多数情况下估计区间的不确定性水平仅略大于真实区间的不确定性水平，但概率与区间混合时会导致模型输出响应的不确定性水平过高，从而使得模型可信度大幅降低。
目前模型确认方法广泛应用于评价和提高建模可信度，最早由美国能源部应用于战略武器管理的可靠性评估和决策[3-4]。由于工程领域对仿真分析可信度要求的提高，模型确认方法正大量应用于计算力学、汽车等工程领域[5-6]。随着模型确认技术的应用推广，人们逐渐认识到仅仅实施评估模型精确度的模型确认过程并不能满足工程实际需求，需对未达到要求的模型进行模型修正[7]。
模型确认方法可分为基于贝叶斯理论的贝叶斯方法[8]和基于统计及推断方法的非贝叶斯方法[9-10]两大类。KENNEDY等[8]提出了基于贝叶斯理论的模型修正方法；LIU等[11]针对热传导问题的模型修正，采用贝叶斯方法来提高模型精度；HASSELMAN等[12]针对汽车碰撞模型提出了一种基于模型响应值均方差结果的修正方法。
近年来，为确保仿真工作具有实际应用价值和意义，对模型确认问题的研究已受到国内学者们的重视。张保强等[13]将贝叶斯方法用于圣地亚热传导问题的模型修正中，并建立相应的贝叶斯框架；何成等[14]分析了基于径向基模型的不确定性结构动力学模型非概率型区间修正方法；肖钊等[15]针对试验数据较少的情况，利用区间方法量化不确定性，并提出了对应模型确认方法；方圣恩等[16]提出了针对结构参数不确定性的随机模型优化方法；姜东等[17]基于区间分析提出了不确定性结构动力学模型修正方法。综上可知，人们已开展了一些模型确认问题的工作，并取得了一定成果，但针对概率与区间混合不确定性情况的研究并不多，且总体上就模型确认问题并未达成统一共识。
由于存在不确定性传播的问题，在概率与区间混合不确定性情况下，模型输出响应的数值结果为非精确概率。本文通过数值结果非精确概率累积分布函数(cumulative distribution function,CDF)与试验结果经验累积分布函数(empirical cumulative distribution function，ECDF)之间的面积极大值求解模型确认准则参数，并对模型确认结果进行评估，对于不满足确认评估标准的模型，以区间变量表征的不确定性参数为对象实施修正，最后将模型确认方法应用于圣地亚热传导问题的算例中，并验证了所提方法的有效性。
1 参数不确定性模型确认过程
实际工程模型中普遍存在随机不确定性参数、认知不确定性参数、确定性参数混合情况，本文针对区间变量表征认知不确定性参数，概率变量表征随机不确定性参数及确定性参数的混合情况进行了研究分析，得到模型函数可表示为
Y=g(X,Z,M)
(1)
式中，X为区间变量矢量；Z为概率变量矢量；M为确定性变量矢量；Y为模型输出响应(随机变量)。
受不确定性混合影响，模型中只要存在参数不确定性水平略大于真实水平的情况，就会使模型输出响应的不确定性水平过高，从而需进行模型确认以保证响应准确度和建模可信度。
模型确认的目的是量化数值模型与真实物理系统的差异程度，并基于差异程度确定模型预测精度。在模型确认过程中，对于未达到模型确认要求的数值模型，需通过模型修正以减小模型误差，从而使数值模型满足预期要求。在参数不确定性模型中对模型参数进行修正，概率与区间混合不确定性情况的修正参数为区间变量表征的不确定性参数。
真实物理系统的量化表征是以输出响应的试验数据为基础，响应试验误差会直接影响确认结果的可信度，因此本文将响应试验误差视为数值模型的随机不确定性参数来开展模型确认过程。模型确认实施步骤包括模型确认试验，不确定量化，应用确认准则进行模型确认评估，对不满足要求的模型进行参数修正，以及模型应用等，见图1。
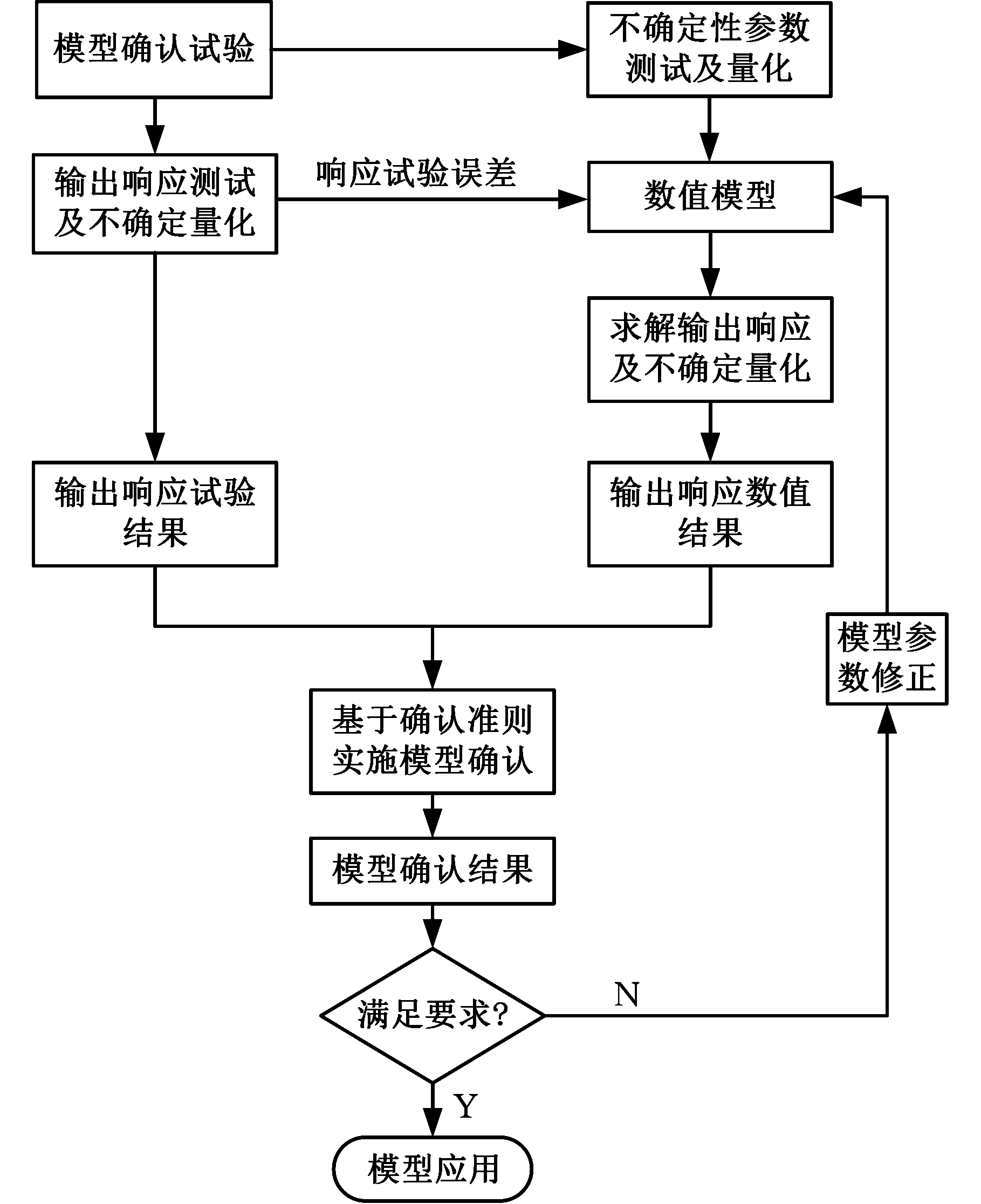
图1 参数不确定性模型确认过程
Fig.1 Validation process of parameteruncertainty model
模型确认试验和确认准则在模型确认过程中至关重要，模型确认试验的设计、执行、分析是以定量确定数值模型及其载体(仿真软件)在多大程度上能够代表实际系统为目的[6]。不同工程实际问题应根据确认的需求对系统、子系统、部件和单元的各个层面分别进行试验测试。模型确认准则主要可分为图像对比准则、频率准则、经典假设检验法、贝叶斯因子、面积度量准则等[18]。在模型确认过程中，需根据实际问题应用合理的确认准则以获得可信的确认结果。
2 概率与区间混合不确定性下参数不确定性模型确认理论
2.1 区间变量
区间变量的数学定义为[19]
XI=[XL,XU]=[x|XL≤x≤XU,x∈R]
(2)
式中，x为实数集变量；XL、XU分别为区间下限和区间上限。
区间变量也可利用区间中点和区间半径来表示，即
XI=[XC-XR,XC+XR]
(3)
式中，XC为区间中点；XR为区间半径。
应用区间变量来量化不确定性，区间可靠度是评价量化结果的指标之一，区间可靠度H可用区间置信系数来定义[20] ，即
H=PXI{XL≤x≤XU}∝XR
(4)
其中，PXI为区间变量XI包含参数所有值的概率。H与区间半径XR成正比(即区间半径XR越大，区间变量的置信水平越高，区间估计越可靠)。
2.2 模型输出响应数值结果
不确定性传播中概率与区间混合不确定性情况下模型的输出响应数值结果为非精确概率，本文采用概率盒(probability box , P-box)来表征[21]。如图2所示，概率盒将上下两条累积分布函数(CDF)作为边界，数学定义为[22]
(5)
式中，
为概率盒变量；FY(y)为概率盒内可能的累积分布函数；
分别为概率盒下边界和上边界；
为最小概率值;y为随机变量Y的任意一个实数值。
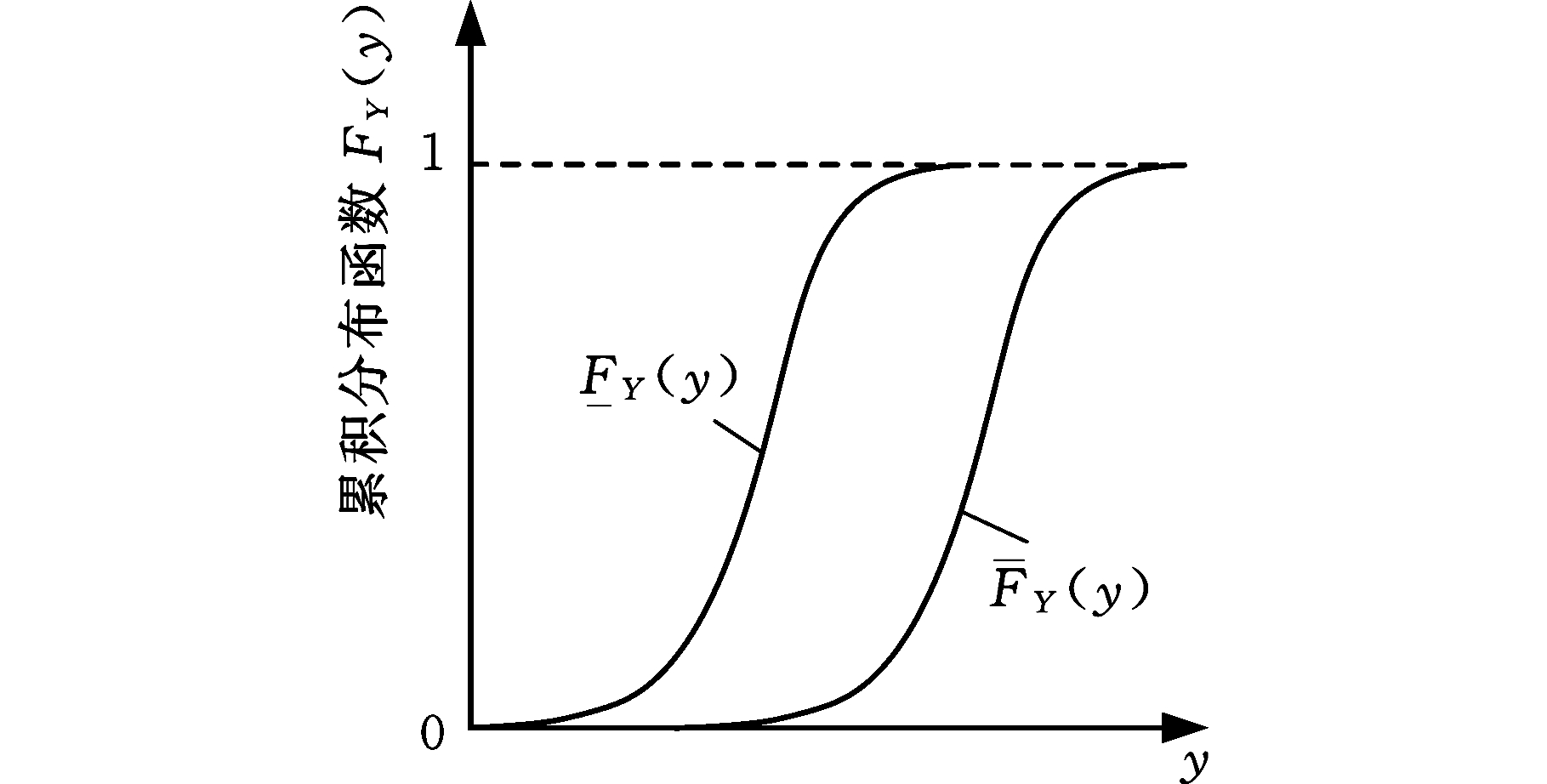
图2 概率盒示意图
Fig.2 Schematic diagram of probability box
2.3 模型确认与评估
面积度量准则[23]是一种有效的模型定量确认准则，以仿真值CDF与试验值ECDF的面积差值作为准则值。为确保概率与区间混合不确定性情况下模型确认的有效性，本文考虑确认准则值的量纲一性，以面积度量准则为基础，根据数值结果概率盒上下边界与试验结果ECDF之间的面积极大值定义了模型确认准则，具体表达式如下：
(6)
式中，VP为模型确认准则参数；max{·}为求解最大集合元素函数;B为输出响应试验数据的中点;Se(y)为响应试验结果ECDF。
以某概率与区间混合不确定性情况为例，假设在某一参数条件下，响应数值结果CDF为概率盒，概率盒边界与试验结果ECDF的面积差值图见图3。其中，
为响应试验结果
为概率盒上边界和下边界；B*为输出响应试验数据中点。由计算可得，该模型确认准则值为
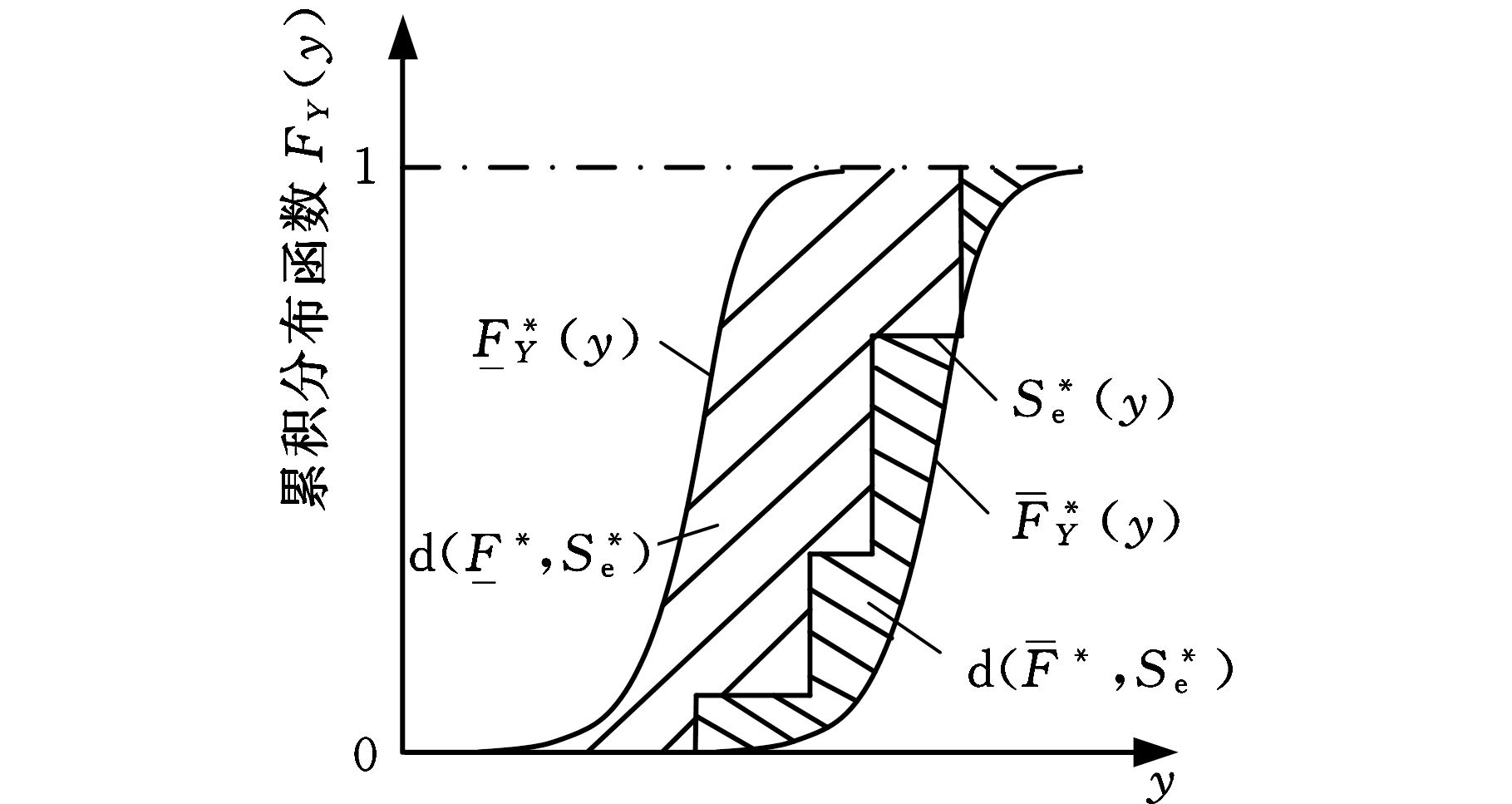
图3 概率盒边界与试验结果ECDF的面积差值图
Fig.3 Different area between probability boxboundary and the ECDF of test results
模型确认准则可量化试验结果与仿真结果的差异，求解得到的VP值越大，表明数值模型和真实物理对象的吻合程度越低，为此提出模型确认评估标准，即
VP≤δ
(7)
其中，δ为确认标准值，根据模型实际应用条件取某一常数值。当数值模型有较高要求时，需设定较小的δ值，反之则可设定较大的δ值。
2.4 模型修正
当确认准则值大于标准值δ时，需对模型参数进行修正。模型参数修正实质为优化待修正参数，本文以模型确认评估标准和模型参数初始值 为约束条件，以待修正区间不确定性参数总置信水平最大为目标实施参数修正，得到优化模型如下：
(8)
式中，H(X)为待修正区间不确定性参数总置信水平函数；Θ为模型参数初始值域。
上述优化模型的求解是一个双层嵌套求解过程，为能够高效地求解优化模型，首先根据式(3)将区间变量XI转换为区间中点XC和区间半径XR的形式，由于置信水平与区间半径成正比，因此目标函数可简化为
遗传算法[24]具有精度高和鲁棒性强等优点，已在工程实际中获大量应用，本文基于简化后的目标函数应用遗传算法求解优化问题，最终获得修正结果。
3 算例(圣地亚热传导问题)
图4为一维瞬态圣地亚热传导模型示意图[25]，数学模型可表示为
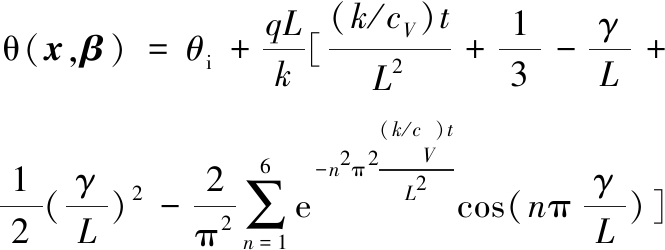
(9)
x=(q,L,t,γ) β=(k,cV)
式中，θi为初始温度，这里为25 ℃；q为热流密度；L为板厚；k为材料热导率；cV为体积热容；γ为表面距离；t为时间；x为受控输入参数矢量；β为待修正参数矢量。
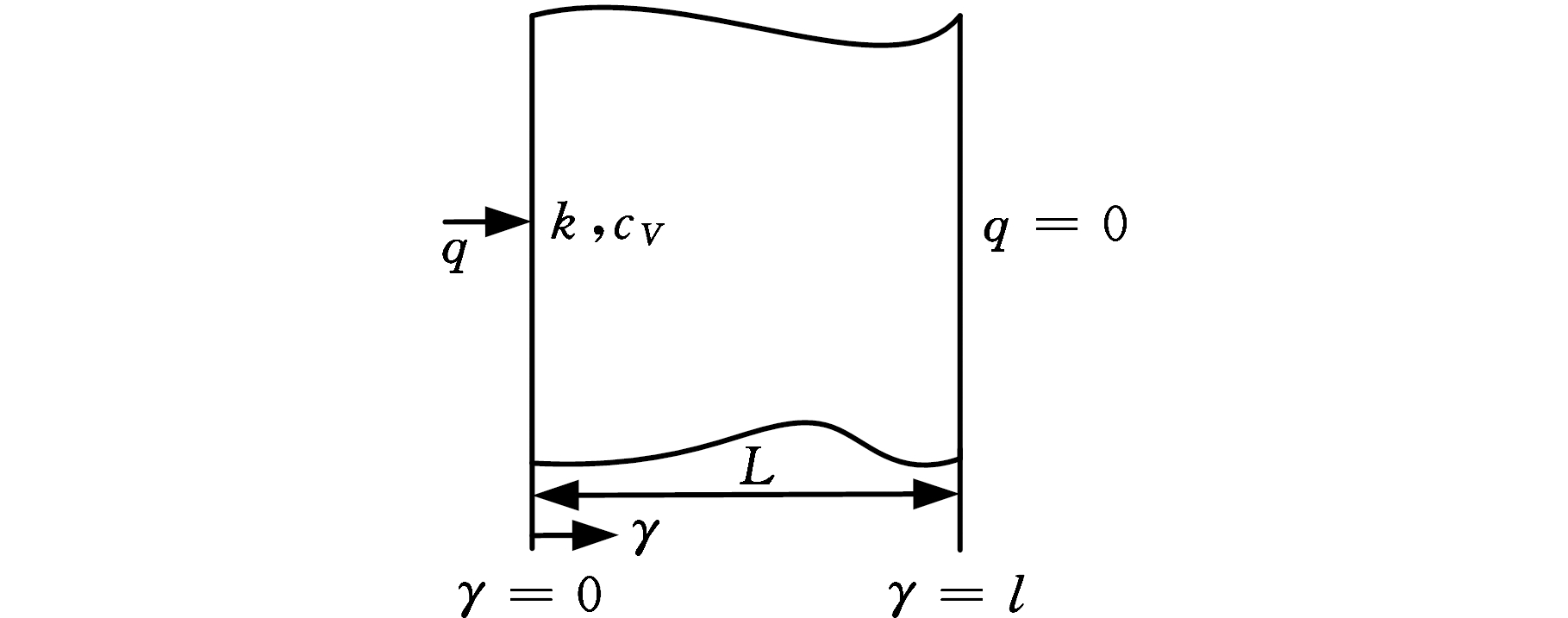
图4 热传导模型示意图
Fig.4 Schematic diagram of thermal challengeproblem model
圣地亚热传导模型的预测目标为受控输入参数矢量x=(3 500 W/m2,0.019 m,1 000 s,0 m)时，温度大于900 ℃的概率小于0.01，即
P{θ(x,β)>900 ℃}<0.01
(10)
圣地亚热传导问题中试验误差无法避免，本文通过考虑模型输出响应温度的试验误差来开展模型确认，则热传导问题数值模型可表示为
θ(x,β,εe)=θ(x,β)+εe
(11)
其中，受控输入参数x为确定性变量矢量；待修正参数β为认知不确定性变量矢量，应用区间变量表征；响应试验误差εe为随机不确定性变量，应用概率分布表征。
模型确认热传导问题试验分为材料特性(material characterization，MC)试验，整体确认(ensemble validation，EN)试验，认证(accreditation validation，AC)试验，所有试验根据数据量的大小分为低水平、中水平和高水平等级。由于高水平试验数据量与其他两个水平的数据量差距较小，为确保模型确认的有效性，故本文选用高水平试验数据进行热传导问题模型确认，试验数据详见文献[25]。
温度对待修正参数有较大影响，本文考虑待修正参数的温度依赖性求解函数方程，分析试验数据可知，体积热容cV为独立变量，则体积热容区间变量的表达式如下：
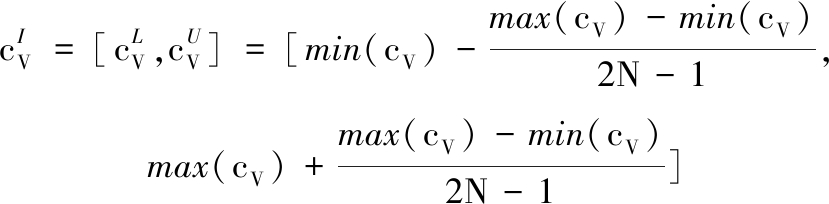
(12)
式中，N为试验数据数量。
材料热导率k对温度存在依赖性，建立关于温度θ的一维线性回归模型，表达式如下：
k=a+bθ+ω
(13)
根据MC试验数据求得参数a为0.051 2，b为2.25×10-5，误差项ω ～ N(0,0.005 32)，根据正态分布求解误差项区间变量形式(即ωI =[μ-3σ, μ+3σ])，得到含区间变量的方程如下：
k=0.051 2+2.25×10-5θ+[μ-3σ，μ+3σ]
(14)
式中，μ为正态分布均值；σ为正态分布标准差。
根据文献[7]可得试验误差εe的分布为εe～N(0,5.252)。
热传导问题模型确认中可用函数表示式来表示预测温度与各参数之间的关系：θ=g(x,β,εe)，将区间变量(式(12)、式(14))及各概率分布代入上述函数表达式，可得热传导问题模型确认方程如下：
(15)
热传导问题模型确认方程是以θ为变量的非线性方程，可进行优化求解。本算例的模型确认标准值设定为δ=0.3，应用所提确认准则进行模型确认，热传导问题模型确认评估的表达式为
(16)
式中，
分别为温度θ概率盒变量下边界和上边界；θe为温度响应的试验数据；Se(θe)为温度响应的试验结果ECDF；Bθ为温度响应试验数据中点。
圣地亚热传导问题设计进行了不同的EN试验和AC试验，EN试验的高水平数据为在0～1 000 s范围内，以间隔100 s选取得到10个时间点的4组试验数据，每组试验重复4次；AC试验高水平数据为在0～1 000 s范围内，以间隔50 s选取得到20个时间点的3组试验数据，每组试验重复2次。表1和表2分别列出了热传导问题各EN试验参数和AC试验参数。
表1 整体确认试验参数
Tab.1 The test parameters of EN
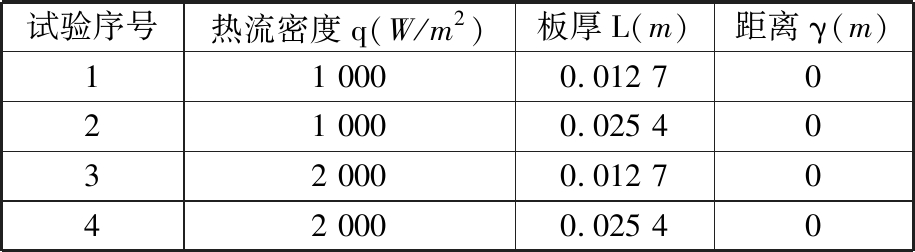
试验序号热流密度q(W/m2)板厚L(m)距离γ(m)11 0000.012 7021 0000.025 4032 0000.012 7042 0000.025 40
表2 认证试验参数
Tab.2 The test parameters of AC
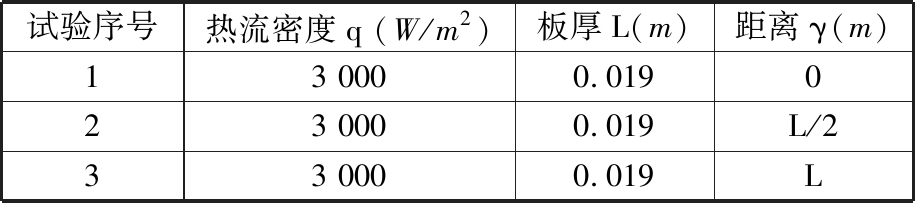
试验序号热流密度q (W/m2)板厚L(m)距离γ(m)13 0000.019023 0000.019L/233 0000.019L
本文综合应用EN试验和AC试验的高水平数据进行模型确认，根据表1和表2中的具体参数值，将不确定性参数表征值代入式(15)，运用双层采样法得到θ的概率盒模型，最后根据式(16)分别求得各时刻下的VP(t)。
图5a为EN试验条件下未修正确认准则的参数曲线图，可以看出，所有试验序号各时刻下的确认准则参数值均小于0.3，满足确认评估要求。图5b为AC试验条件下未修正确认准则的参数曲线图，可以看出，在0～1 000 s范围内AC1试验的确认准则参数值满足要求；而AC2试验的确认准则参数值有部分不满足要求，且t=200 s为确认准则参数曲线极值点(即VP(t=200 s)为0.36>δ)；AC3试验中t=450 s为曲线极值点(即VP(t=450 s)为0.7>δ)，且大部分AC3试验确认准则的参数值不满足要求。
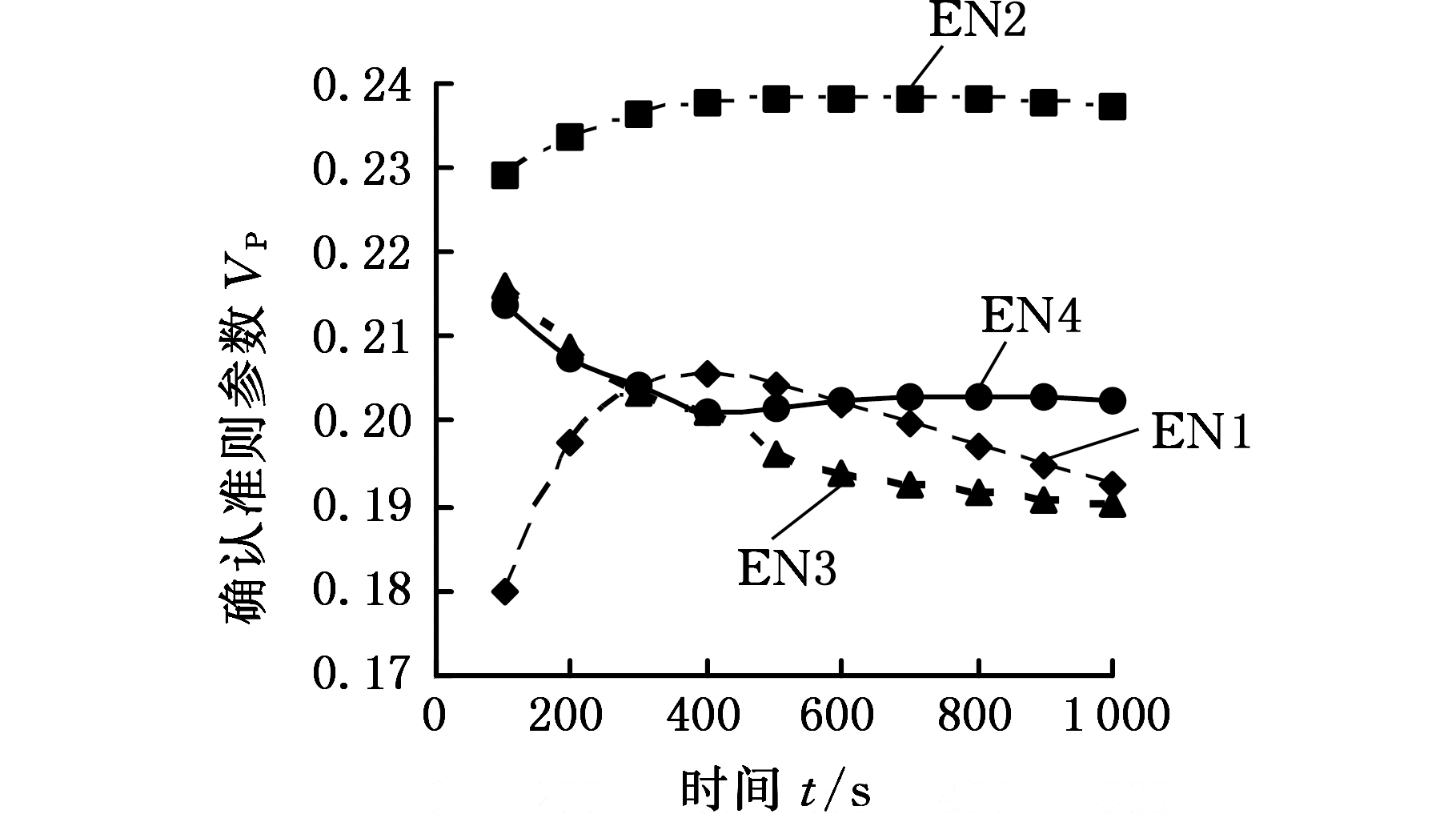
(a)整体确认试验
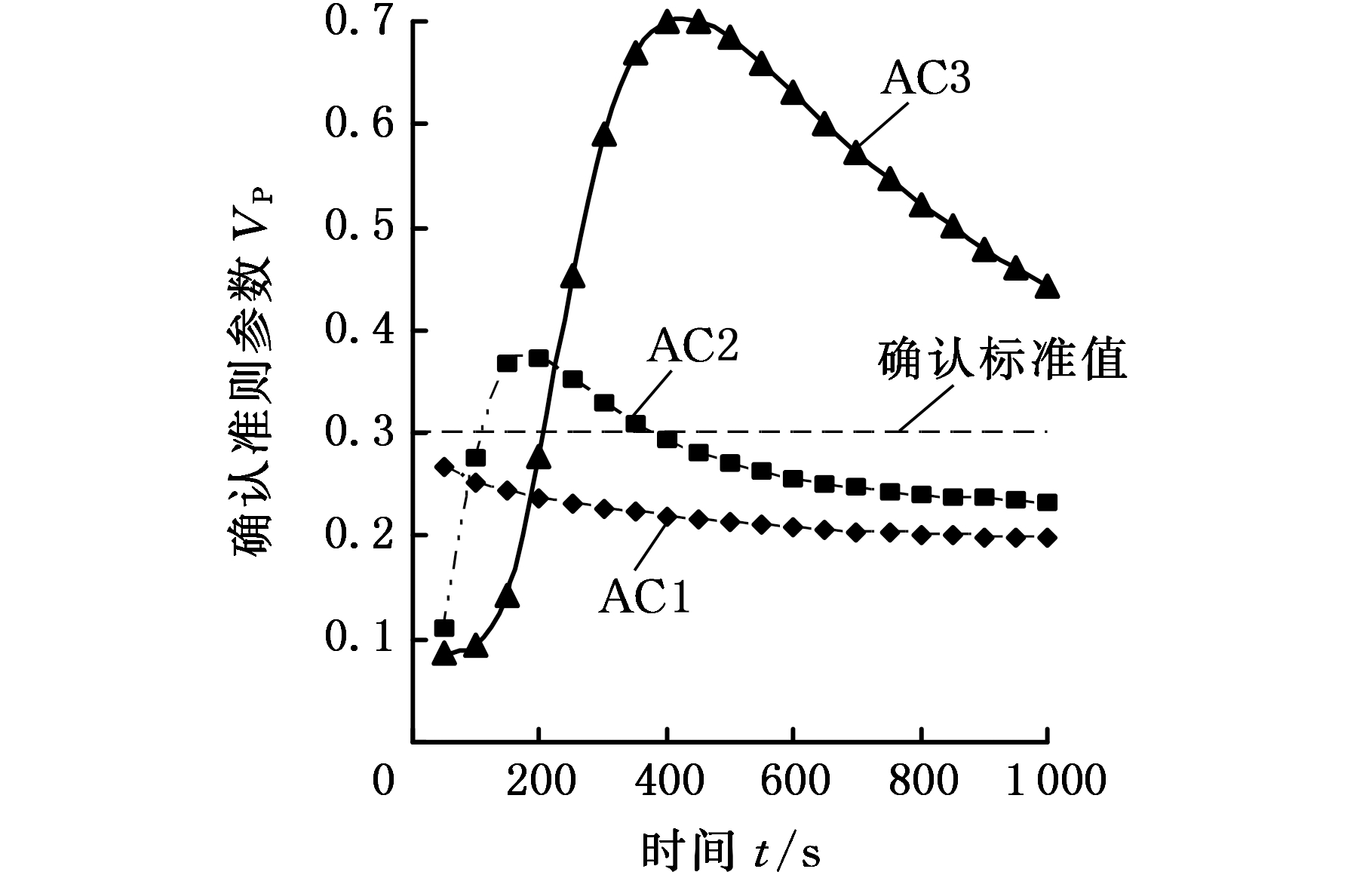
(b)认证试验
图5 未修正模型确认准则参数值
Fig.5 Values of uncorrected model validationcriteria parameters
在热传导问题中，AC2试验和AC3试验的确认准则参数值不满足确认评估要求，应进行模型参数修正。由于AC3试验条件下确认准则参数值不满足要求的比例远大于AC2试验条件下的比例，且AC3试验条件下准则参数值曲线的极值点VP(t=450 s)=0.7大于AC2试验条件下准则参数值曲线极值点VP(t=200 s)=0.36，故依据AC3试验进行模型参数修正。AC3试验的准则参数值曲线为开口向下的抛物线，在t=450 s时达到最高点，所以修正后满足VP(t=450 s)≤δ的条件，就可使所有曲线均满足要求。基于AC3试验条件下t=450 s的确认结果修正模型参数，得到优化模型如下：
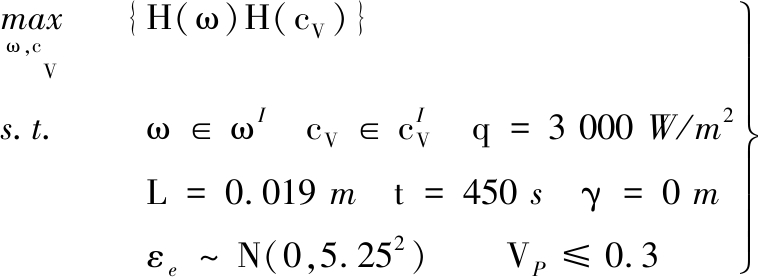
(17)
目标函数经简化后，运用遗传算法求解优化模型，表3为模型参数修正结果，表4为修正前后参数值对比。
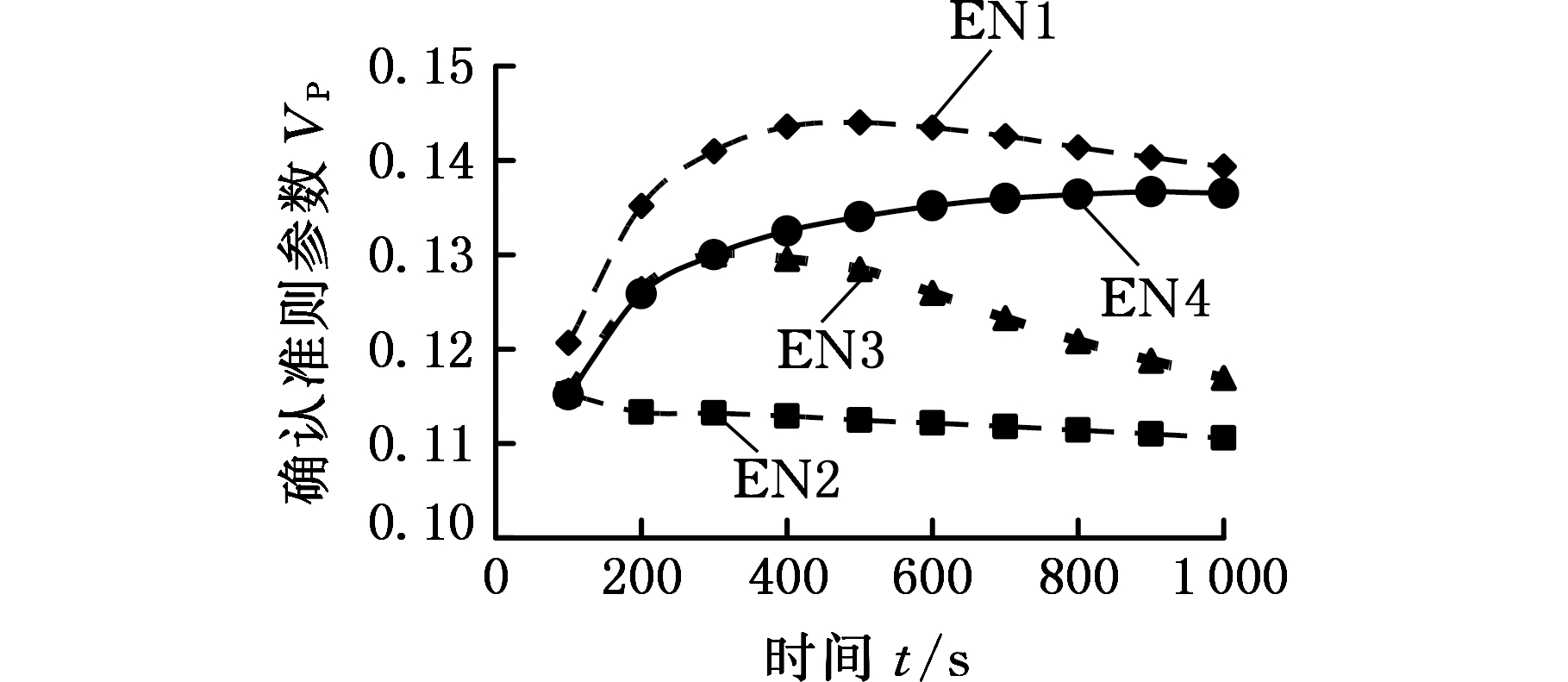
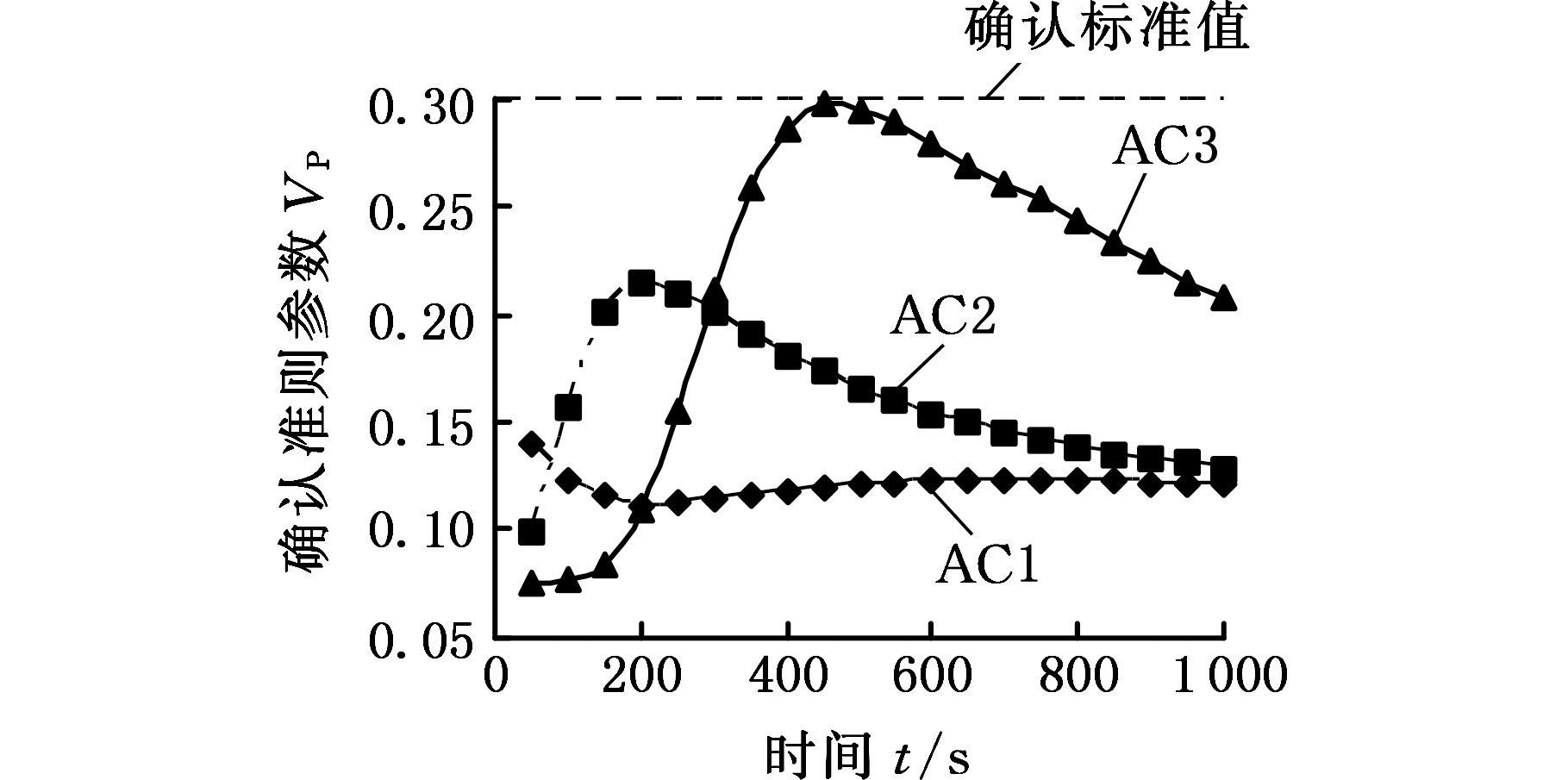
基于修正后参数值进行模型确认，图6a和图6b分别为修正后EN试验和AC试验条件下的模型确认准则参数值曲线。由图6可知，修正后全部确认试验所有时刻点的模型确认准则参数值均小于0.3，数值模型满足使用要求。
表3 模型参数修正结果
Tab.3 The correction results of model parameters
参数区间中点区间半径体积热容cV(J/(m3·℃))4.116×1050.458×105材料热导率误差项ω-0.002 650.012 15
表4 参数修正前后结果对比
Tab.4 Comparison of parameters beforeand after correction
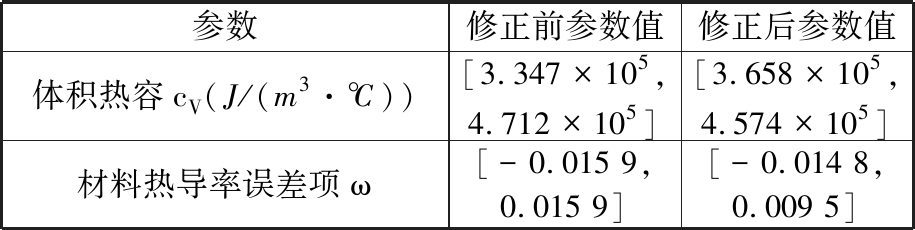
参数修正前参数值修正后参数值体积热容cV(J/(m3·℃))[3.347×105,4.712×105][3.658×105,4.574×105]材料热导率误差项ω[-0.015 9,0.015 9][-0.014 8,0.009 5]
(a)整体确认试验
(b)认证试验
图6 已修正模型确认准则参数值
Fig.6 Values of model validation criteria parametersafter correction
将修正后的模型参数代入式(10)求解，采用蒙特卡罗法抽样(抽样次数为1×106次)可得到失效概率。图7为修正后温度θ的累积分布函数曲线，预测结果见表5。由表5可知，模型未修正时，温度超过900 ℃的概率为0.078 1，模型修正后，温度超过900 ℃的概率为0.016 2，预测精度得到明显提高。
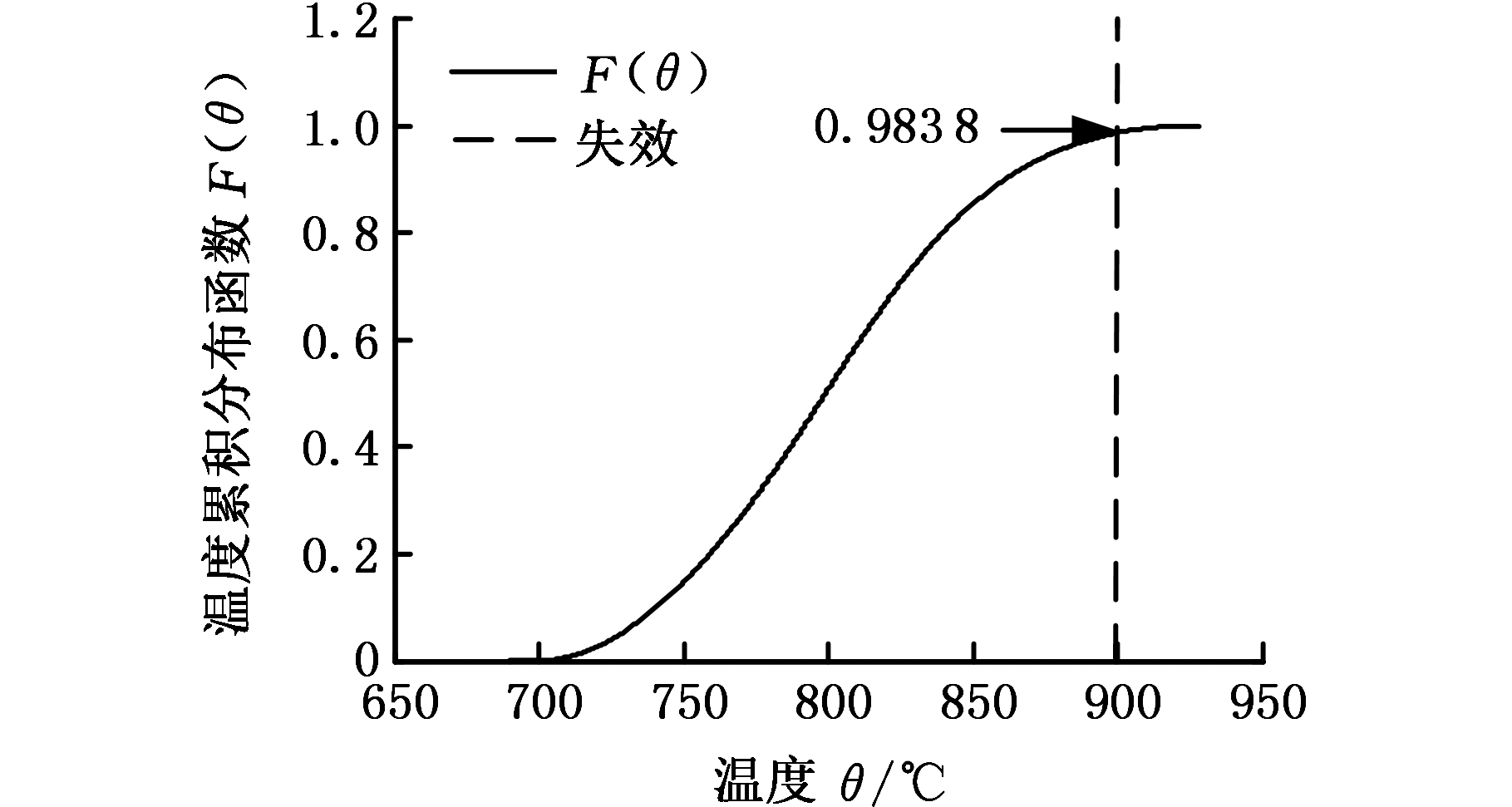
图7 修正后温度的累积分布曲线
Fig.7 The CDF curve of temperature after correction
表5 预测结果对比
Tab.5 Comparison of predictive results
模型预测未修正修正后P{θ(x,β)>900 ℃}0.078 10.016 2
热传导问题中失效概率的目标要求不能大于0.01，采用本文方法得到的模型预测概率结果也不满足要求，这与同类文献[11,26-28]的结论一致。采用不同方法的模型修正对比见表6，其中文献[11,27]基于贝叶斯原理实施模型修正。
表6 不同方法模型修正对比
Tab.6 Comparison of model correction based ondifferent methods
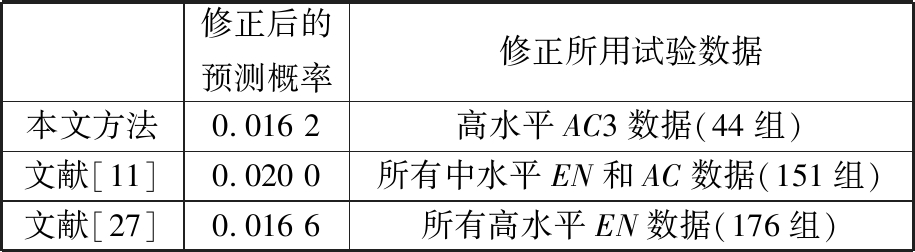
修正后的预测概率修正所用试验数据本文方法0.016 2高水平AC3数据(44组)文献[11]0.020 0所有中水平EN和AC数据(151组)文献[27]0.016 6所有高水平EN数据(176组)
由表6可知，三种方法的修正后模型预测概率十分相近，但文献[11,27]所用试验数据量是本文方法所用试验数据量的3倍以上。基于贝叶斯的模型修正方法以增加试验数据量为基础，且模型参数先验分布的确定存在较大主观性，因此，在工程实际试验难度较大、试验成本较高的情况下，本文方法具有明显的优势。
4 结论
(1)在概率与区间混合不确定性情况下，本文的模型确认准则依据数值结果概率盒边界与试验结果经验累积分布函数之间的面积极大值进行定义，可获得有效可信的模型确认结果值，为后续确认评估及修正奠定了基础。
(2)以待修正区间不确定性参数总置信水平最大为修正目标，以模型确认评估标准和模型参数初始值为约束条件，目标函数简化后应用遗传算法修正模型参数，获得的修正结果具有可信性。
(3)将本文方法应用于圣地亚热传导问题，经模型确认后热传导模型的预测精度有明显提高，模型可信度和响应准确度有较大提升，获得了与同类文献相同的预测结果。修正后模型预测概率与基于贝叶斯的模型修正方法得到的修正后预测概率的结果十分相近，但本文方法所用试验数据量有明显减小。在试验难度较大、试验成本较高的情况下，本文方法比基于贝叶斯的模型修正方法更具优势，具有较好的应用前景。
[1] ELISHAKOFF I，COLOMBI P.Combination of Probabilistic and Convex Models of Uncertainty When Scare Knowledge Is Present on Acoustic Excitation Parameters[J].Computer Methods in Applied Mechanics & Engineering，1993，104：187-209.
[2] 姜潮，李文学，王彬，等.一种针对概率与非概率混合结构可靠性的敏感性分析方[J].中国机械工程，2013，24(19)：2577-2583.
JIANG Chao，LI Wenxue，WANG Bin，et al.A Sensitivity Analysis Method for Probabilistic and Non-probabilistic Hybrid Structures[J]. China Mechanical Engineering，2013，24(19)：2577-2583.
[3] American Institute of Aeronautics and Astronautics，AIAA-G-077-1998，Guide for the Verification and Validation of Computational Fluid Dynamics Simulations[S]. Reston：AIAA，1998.
[4] American Society of Mechanical Engineers.ASME V&V 10-2006，Guide for Verification and Validation in Computational Solid Mechanics[S].New York：ASME，2006.
[5] American Society of Mechanical Engineers.ASME V&V 10.1-2012，an Illustration of the Concepts of Verification and Validation in Computational Solid Mechanics[S].New York：ASME，2012.
[6] OBERKAMPF W L，ROY C J.Verification and Validation in Scientific Computing[M].New York：Cambridge University Press，2010.
[7] XIONG Y，CHEN W，TSUI K，et al.A Better Understanding of Model Updating Strategies in Validating Engineering Models[J].Computer Methods in Applied Mechanics and Engineering，2009，198(15)：1327-1337.
[8] KENNEDY M C，OHAGAN A. Bayesian Calibration of Computer Models[J]. Journal of the Royal Statistical Society Series B-statistical Methodology，2001，63(3)：425-464.
[9] HILLS R G，DOWDING K J. Multivariate Approach to the Thermal Challenge Problem[J].Computer Methods in Applied Mechanics and Engineering，2008，197(29)：2442-2456.
[10] BRANDYBERRY M D.Thermal Problem Solution Using a Surrogate Model Clustering Technique[J].Computer Methods in Applied Mechanics and Engineering，2008，197(29)：2390-2407.
[11] LIU F，BAYARRI M J，BERGER J Q，et al.A Bayesian Analysis of the Thermal Challenge Problem[J].Computer Methods in Applied Mechanics and Engineering 2008，197(29/32)：2121-2136.
[12] HASSELMAN T，YAP K，LIN C，et al.A Case Study in Model Improvement for Vehicle Crashworthiness Simulation[C]//23rd International Modal Analysis Conference.Orlando，2005:89-98.
[13] 张保强，陈国平，郭勤涛.模型确认热传导挑战问题求解的贝叶斯方法[J].航空学报，2011，32(7)：1202-1209.
ZHANG Baoqiang，CHEN Guoping，GUO Qintao.A Bayesian Method for Solving the Problem of Heat Conduction Challenge[J].Journal of Aeronautics，2011，32(7)：1202-1209.
[14] 何成，陈国平，何欢.径向基模型的不确定性模型区间修正与确认[J].机械工程学报，2013，49(11)：128-134.
HE Cheng，CHEN Guoping，HE Huan.Interval Verfication and Validation of Uncertainty Model of Radial Basis Model[J]. Journal of Mechanical Engineering，2013，49(11)：128-134.
[15] 肖钊，韩旭，杨刚.基于区间技术的模型确认方法及应用[J].机械工程学报，2014，50(14)：177-184.
XIAO Zhao，HAN Xu，YANG Gang.Model Validation and Its Application Based on Interval Techniques [J].Chinese Journal of Mechanical Engineering，2014，50(14)：177-184.
[16] 方圣恩，林友勤，夏樟华.考虑结构参数不确定性的随机模型修正方法[J].振动、测试与诊断，2014，34(5)：832-837.
FANG Shengen，LIN Youqin，XIA Zhanghua.Considering the Uncertainty of Structural Parameters of Stochastic Model Verfication Method[J].Journal of Vibration Measurement and Diagnosis，2014，34 (5)：832-837.
[17] 姜东，费国庆，吴邵庆.基于区间分析的不确定性结构动力学模型修正方法[J].振动工程学报，2015，28(3)：352-358.
JIANG Dong，FEI Guoqing，WU Shaoqing.A Verfication Method for Uncertainty Structural Dynamic Model Based on Interval Analysis[J].Journal of Vibration Engineering，2015，28(3)：352-358.
[18] LIU Y，CHEN W，ARENDT P D，et al.Toward a Better Understanding of Model Validation Metrics[J].Journal of Mechanical Design,2011,133(7) :1-13.
[19] MOORE R E.Methods and Applications of Interval Analysis[M].London：Prentice-Hall Inc，1979.
[20] 茆诗松，王静龙，濮晓龙.高等数理统计[M]. 北京：高等教育出版社，2006.
MAO Shisong，WANG Jinglong，PU Xiaolong.Advanced Mathematical Statistics[M].Beijing: Higher Education Press，2006.
[21] FERSON S，HAJAGOS J.Arithmetic with Uncertain Numbers：Rigorous and (often) Best Possible Answers[J]. Reliability Engineering & System Safety，2004，85(1)：135-152.
[22] FERSON S，KREINOVICK V，GINZBURG L R，et al.Constructing Probability Boxes and Dempster-shafer Structures[R]. Livermore：Sandia National Laboratories，2003.
[23] Ferson S， Oberkampf W L，Ginzburg L.Model Validation and Predictive Capability for the Thermal Challenge Problem[J]. Computer Methods in Applied Mechanics and Engineering 2008，197：2408-2430.
[24] GOLDBERG D E.Genetic Algorithms in Search，Optimization and Machine Learning[M].New Jersey: Addison-Wesley,1989：19-89.
[25] DOWDING K J，PILCH M，HILLS R G，et al. Formulation of the Thermal Problem[J]. Computer Methods in Applied Mechanics and Engineering，2008，197(29/32)：2385-2389.
[26] BRANDYBERRY M D.Thermal Problem Solution Using a Surrogate Model Clustering Technique[J].Computer Methods in Applied Mechanics and Engineering，2008，197(29/32)：2390-2407.
[27] MCFARLAND J，MAHADEVAN S. Multivariate Significance Testing and Model Calibration under Uncertainty[J]. Computer Methods in Applied Mechanics and Engineering，2008，197(29/32)：2467-2479.
[28] RUTHERFORD B M.Computational Modeling Issues and Methods for the“Regulatory Problem”in Engineering Solution to the Thermal Problem[J].Computer Methods in Applied Mechanics and Engineering，2008，197(29/32)：2480-2489.
