0 引言
速度规划是高档数控系统运动轨迹控制的关键技术之一,是评价数控系统性能的重要指标,直接影响数控机床的加工效率和加工质量。高速、高质量加工对数控机床的加减速控制能力提出了更高的要求,一方面要求刀具能够在最短的时间内,从当前位置点精确地移动到下一位置点;另一方面要求在刀具移动的过程中,保证数控机床平稳运行,避免因超过机床最大加减速能力而引起冲击、失步、超程或振动。
在对离散小线段进行加工时,如果以较高的速度通过相邻小线段间的拐角,可能会因为超出驱动轴最大加速度而引起机床振动,降低加工质量。最简单的解决方法是将连续小线段的起始和终止速度设置为零,但驱动轴的频繁起停会引起机床振动,影响加工质量,同时也会降低加工效率。彭芳瑜等[1]、黄昕等[2]在满足轮廓误差、机床加减速性能和最大加速度等约束条件下,通过计算相邻小线段拐角处所允许的最大速度,实现加工路径间的连续转接,因此,如何在满足轮廓误差和机床动态性能等的前提下,尽可能提高加工速度是数控系统速度规划技术的重要研究内容。
近年来,国内外学者针对速度规划技术做了大量研究,常见的规划方式有直线加减速控制方法[3]和指数加减速控制方法[4]。这两种方式控制简单,计算量小,但存在加速度频繁突变的情况,导致机床振动。ERKORKMAZ等[5]提出S型曲线加减速控制算法,将加速度的变化率限制在某一范围内,来减小对机床的冲击,但加加速度依然存在突变。冷洪滨等[6]采用三次多项式曲线替代S型曲线进行速度规划,在加减速过程中实现了加加速度的连续,但加减速的开始和结束处仍然存在加加速度突变的情况。为此,一些研究人员提出四次多项式型[7-8]、五次多项式型[9-11]和三角函数型加减速算法[12-15],以进一步提高控制柔性,实现速度、加速度和加加速度的平滑控制。但上述方法的实现过程比较复杂,涉及到多个参数,需要大量的时间进行数值计算。这些算法多采用离线的方式进行速度规划,在加工过程中,当加工参数发生改变时,数控机床无法及时地做出响应,并不能很好地满足实际加工需求。
本文在上述研究工作的基础上,提出了一种实时柔性加减速控制算法。首先,在自适应前瞻处理中,确定离散小线段拐角处允许通过的最大速度,并保证小线段两端速度的可达性;然后,通过采用预测校正的方式,实时计算下一插补周期的进给速度,实现速度和加速度的连续变化、加加速度的有界变化。同时,如果在加工过程中机床参数或状态发生了改变,动态修调模块能在满足柔性加减速控制的条件下,对当前前瞻结果和速度规划结果做出调整,从而使得进给速度可及时地进行响应。
1 前瞻处理算法
高档数控系统中,前瞻是实现高速高精加工不可或缺的功能,它的主要任务是确定加工路径中相邻小线段拐角处的最大进给速度,保证小线段两端速度的可达性,实现最优速度规划,提高加工效率。
前瞻处理算法由前瞻缓冲区的创建、拐角最大速度的计算、加减速可行性判断、前瞻终止条件、前瞻初始化组成。
1.1 前瞻缓冲区的创建
图1所示为前瞻处理算法所采用的前瞻缓冲区,该缓冲区能够存储N条小线段。本算法使用小线段数组micro_lines[N]来表示该前瞻缓冲区,其中小线段的数据结构如下:
struct MICRO_LINE //记录小线段信息
{
double s[]; //记录起点坐标
double e[]; //记录终点坐标
double l; //记录段长
double vs; //记录初速度
double ve; //记录末速度
double vs_max; //记录起点拐角最大速度
double ve_max; //记录终点拐角最大速度
};
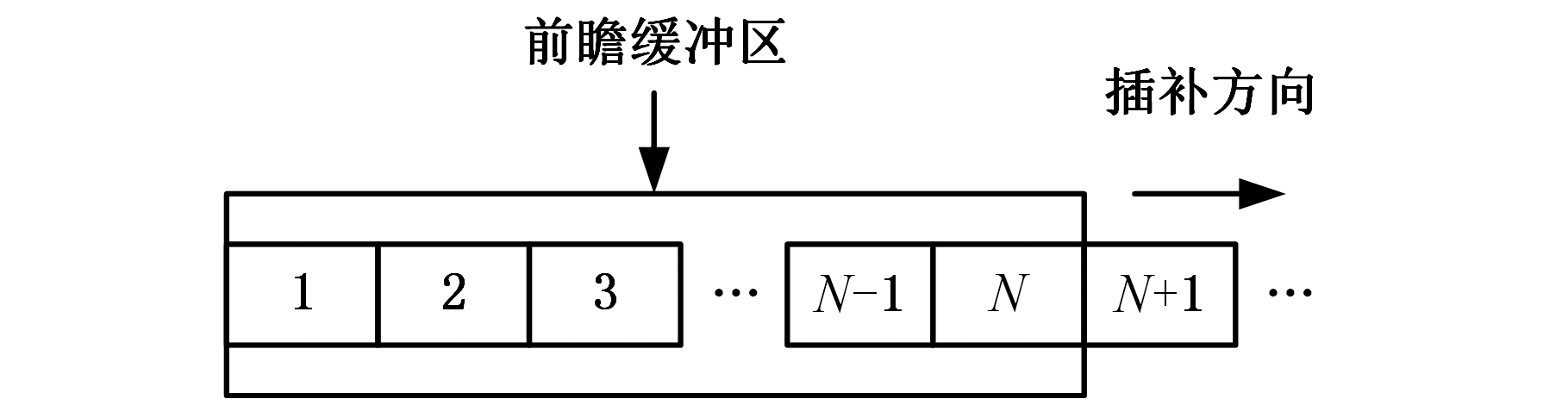
图1 前瞻缓冲区
Fig.1 Look-ahead buffer
1.2 拐角最大速度的计算
为提高数控系统的加工效率,需要在满足伺服系统最大加速度和系统最大轮廓误差的条件下,计算相邻小线段拐角处的最大进给速度。
以XY二维空间为例,如图2所示,AB和BC为由两条小线段表示的连续加工路径,加工方向为A→B→C。
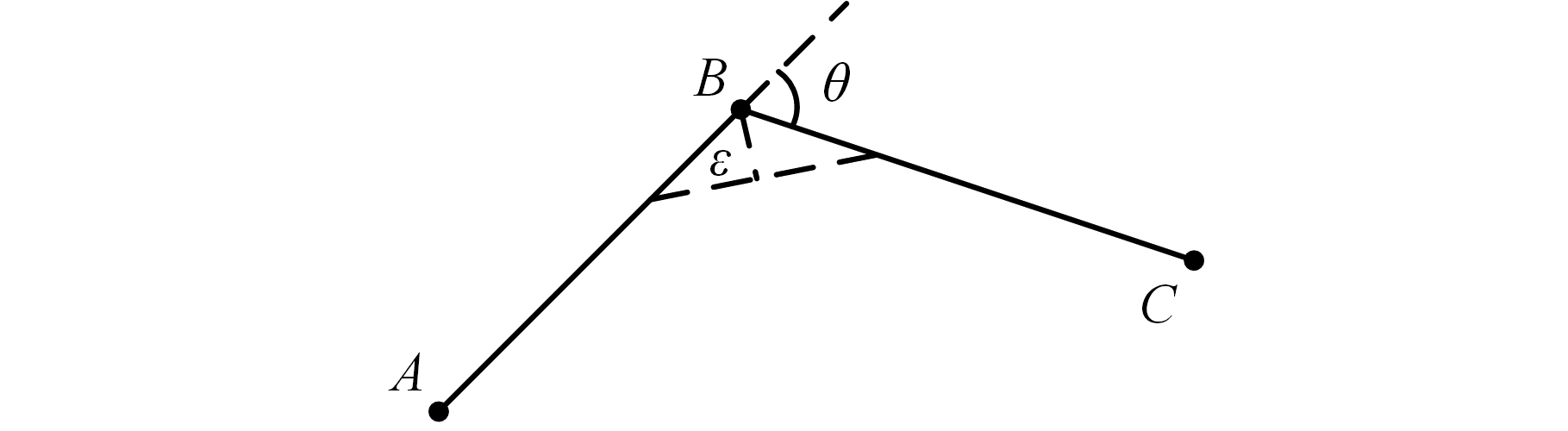
图2 拐角最大速度的计算
Fig.2 Maximum velocity calculation of corner
假设加工过程中系统允许的最大轮廓误差为ε,伺服系统为不产生跟随误差的理想系统,X轴、Y轴方向上所允许的最大加速度分别为aX_max、aY_max,插补周期为T,则拐角∠ABC处所允许的最大加工速度为[16]
式中,α为向量AB与X轴正向之间的夹角;β为向量BC与X轴正向之间的夹角;θ为向量AB与向量BC之间的夹角。
XYZ三维空间中拐角最大速度的计算方法与XY二维空间的情况类似,假设加工路径如图2所示,则拐角∠ABC处所允许的最大加工速度为
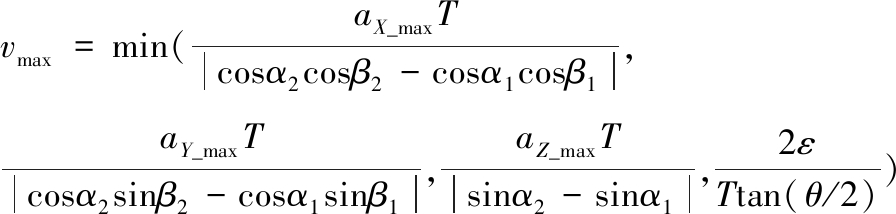
式中,α1为向量AB与XY平面的夹角;β1为向量AB在XY平面上的投影与X轴正向之间的夹角;α2为向量BC与XY平面的夹角;β2为向量BC在XY平面上的投影与X轴正方向之间的夹角;aZ_max为伺服系统在Z轴方向上所允许的最大加速度。
1.3 加减速可行性判断
为了确定小线段拐角处的最终速度,需要进行加减速可行性判断,其处理步骤如下。
(1)假设当前小线段的数组下标为q,系统最大进给速度为F。如果q>N,结束加减速可行性判断;否则,令当前小线段终点处的拐角限制速度v_min=min(micro_lines[q].ve_max, F),其中,micro_lines[q].ve_max为当前小线段的末速度。
(2)如果micro_lines[q].vs<v_min,进入步骤(3);如果micro_lines[q].vs>v_min,则进入步骤(4);否则,令micro_lines[q].ve=v_min,micro_lines[q+1].vs= v_min,结束加减速可行性判断。
(3)正向加速可行性判断。按图3所示的加速度曲线进行加速,计算加速距离l′。如果l′> micro_lines[q].l,则末速度不可达,反求出能够加速到的最大速度ve′,令micro_lines[q].ve= micro_lines[q+1].vs=ve′;否则,令micro_lines[q].ve= v_min,micro_lines[q+1].vs=v_min;结束加减速可行性判断。
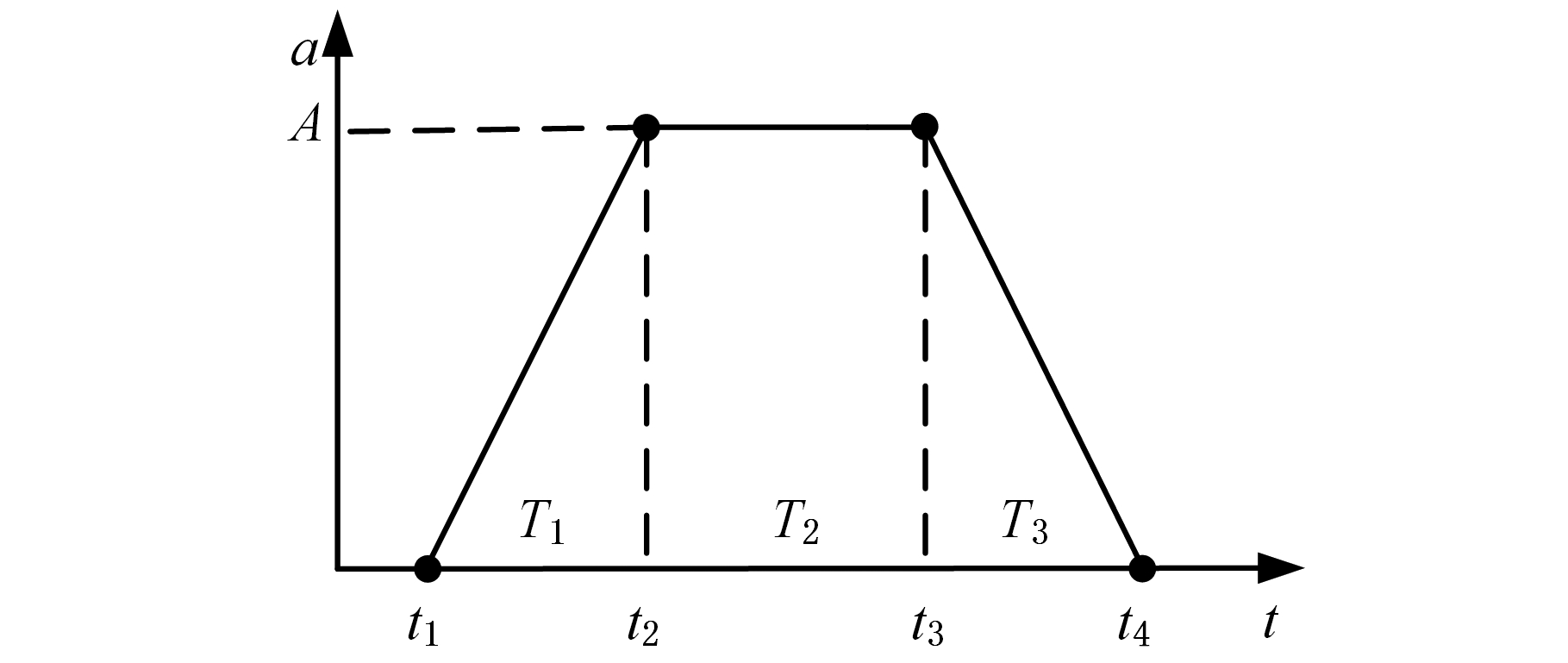
图3 加速度曲线图
Fig.3 Acceleration curve
(4)反向加速可行性判断。按图3所示的加速度曲线进行反向加速,计算加速距离l′。如果l′<micro_lines[q].l,表明满足加减速可行性条件,令micro_lines[q].ve=v_min,micro_lines[q+1].vs= v_min,并结束当前加减速可行性判断处理;否则,说明初速度不可达,求出能够加速到的最大速度vs′,并令micro_lines[q].ve=v_min,micro_lines[q+1].vs=v_min,micro_lines[q].vs= micro_lines[q-1].vs=vs′,令r=q-1,进入步骤①。
①如果r≤1,结束加减速可行性判断。
②如果micro_lines[r].vs>micro_lines[r].ve,按图3所示的加速度曲线进行反向加速,计算加速距离l′,进入步骤③;否则,结束加减速可行性判断。
③如果l′>micro_lines[q].l,则初速度不可达,求出能够加速到的最大速度vs′,并令micro_lines[r].vs=vs′,micro_lines[r-1].ve=vs′,r←r-1,进入步骤①;否则,结束加减速可行性判断。
1.4 前瞻终止条件
假设当前小线段的数组下标为q,v′为计算得到的当前小线段末速度,如果v′≥micro_lines[q].ve,则本次前瞻处理结束。
1.5 前瞻初始化
当数控系统读入NC数控加工文件后,需要进行前瞻初始化,其处理步骤如下:
(1)向前瞻缓冲区中读入N条小线段,将首段的初速度和末段的末速度设置为零,即micro_lines[1].vs=micro_lines[N].ve=0。
(2)按照1.2节所述方法,计算前瞻缓冲区中N个小线段拐角处的最大进给速度。
(3)按照1.3节所述方法,对前瞻缓冲区中的N个小线段进行加减速可行性判断,确定每个拐角处的最终速度。
1.6 前瞻处理
前瞻处理算法的流程如图4所示,其处理步骤如下:
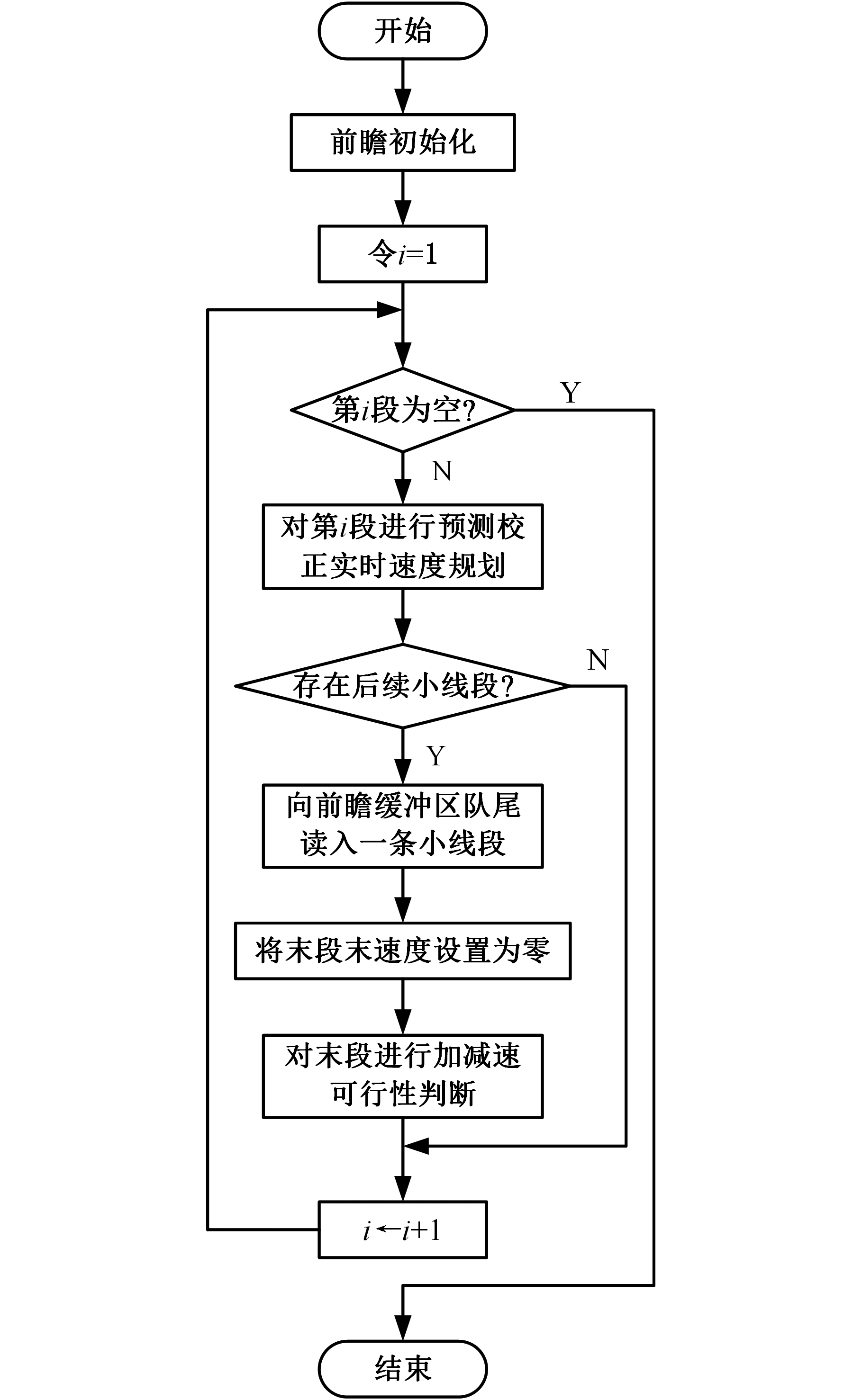
图4 前瞻处理流程图
Fig.4 Look-ahead proccessing flow chart
(1)数控系统读入NC数控加工文件后,进行前瞻初始化。
(2)进入第2节预测校正实时速度规划算法,对前瞻缓冲区中的首段进行实时速度规划。
(3)如果存在后续小线段,则向前瞻缓冲区队尾读入一条小线段,令micro_lines[N].ve=0,micro_lines[N].ve_max=0,计算前瞻缓冲区内第N-1段和第N段拐角处的最大进给速度vt,并令micro_lines[N].vs_max=micro_lines[N-1].ve_max=vt。然后,令q=N,按1.3节所述方法,进行加减速可行性判断。
(4)如果前瞻缓冲区内没有小线段,则结束前瞻处理;否则,进入步骤(2)。
2 预测校正实时的速度规划算法
预测校正实时,速度规划算法利用前瞻处理,以预测的方式,计算下一插补周期进给速度,并依据机床动态性能,校正下一插补周期的速度、加速度和加加速度,然后预测柔性速度规划的可行性,根据预测结果来确定下一步操作,如进行加速插补一步处理、加速处理或减速处理。该算法能够实现进给速度的实时计算,并保证速度曲线光滑、加速度曲线连续、加加速度曲线有界。该算法由预测减速、加速和减速三个模块组成,其算法流程如图5所示。
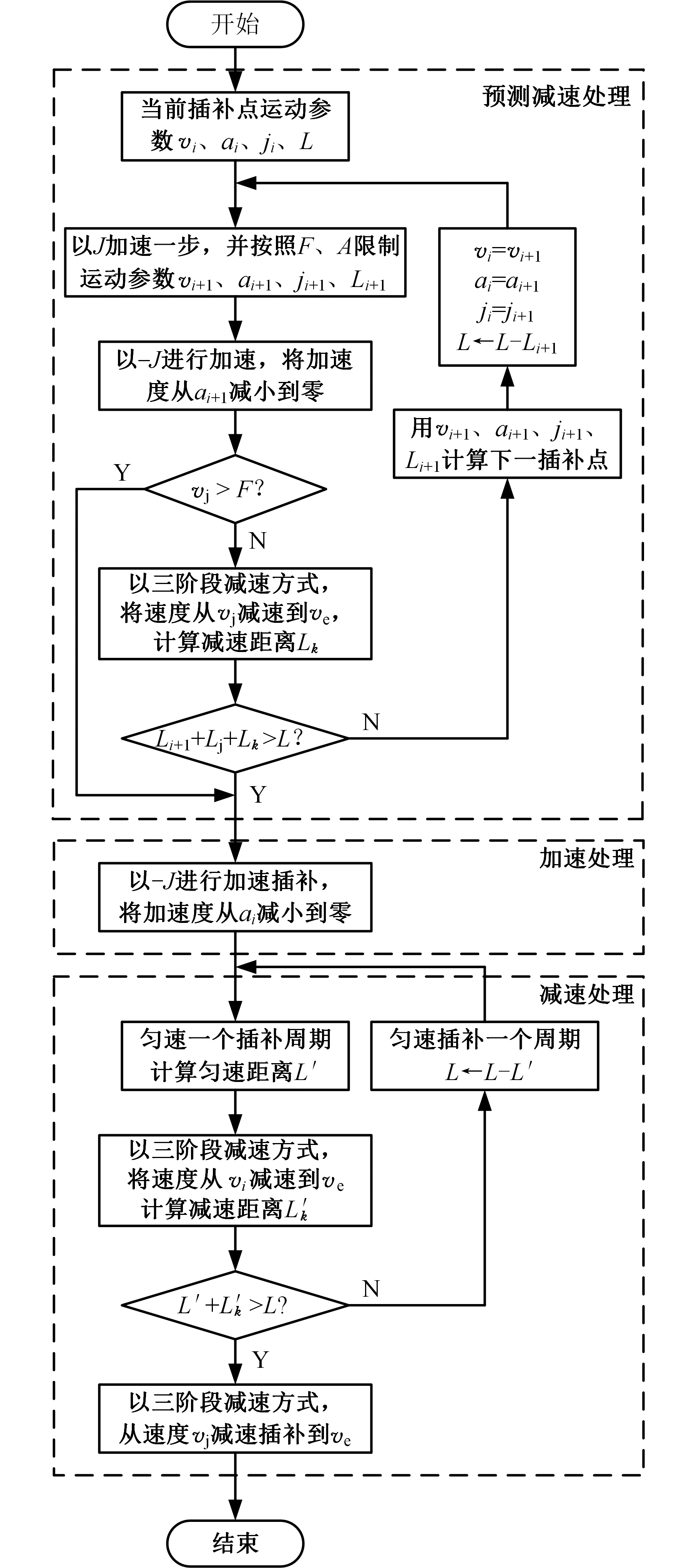
图5 速度规划算法流程图
Fig.5 Velocity planning algorithm flow chart
2.1 预测减速处理
加工过程中,速度、加速度和加加速度的突变会对机床造成冲击,引起振动。因此,在速度规划时,需要寻找减速点,提前进行减速,保证各驱动轴不超过其最大加减速能力。
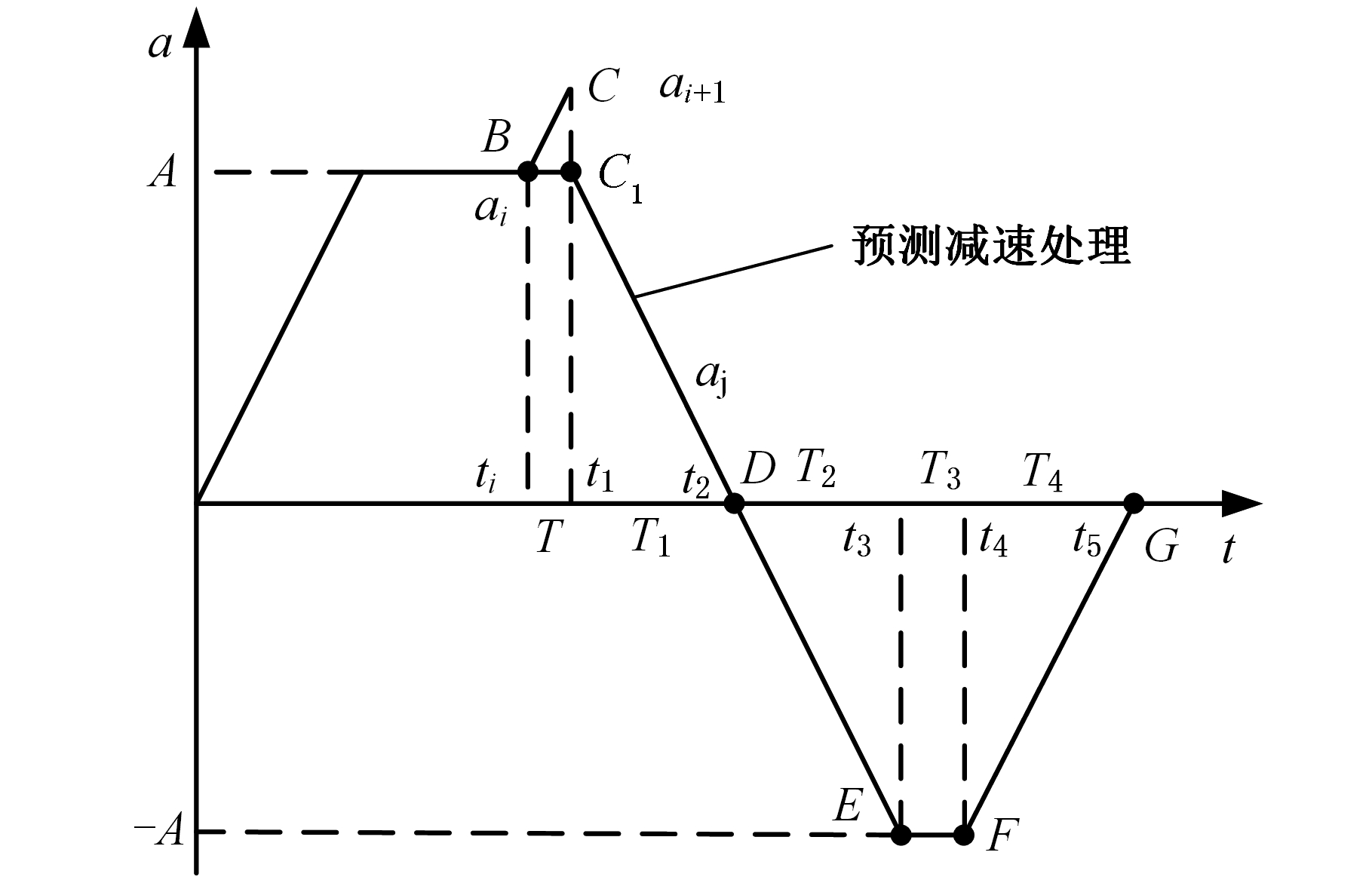
假设系统最大进给速度为F,各个驱动轴的最大加速度为A,最小加速度为-A,最大加加速度为J,最小加加速度为-J,插补周期为T,当前插补周期的速度、加速度和加加速度分别为vi、ai、ji,末速度为ve,剩余距离为L。经过预测减速处理后,其速度和加速度曲线如图6所示,B-C为加加速阶段;B-C1为匀加速阶段;C1-D为减加速阶段,加速度从最大值减小到零;D-E-F-G为减速阶段,加速度先减小到最小值,然后增大,当加速度增大为零时,达到末速度;具体的预测减速处理流程如下。
(1)假设当前插补周期的速度、加速度和加加速度分别为vi、ai、ji,剩余距离为L,以最大加加速度J预加速一个插补周期,如图6中B-C段所示,则下一插补周期的速度vi+1、加速度ai+1、加加速度ji+1和所走过的距离Li+1分别为
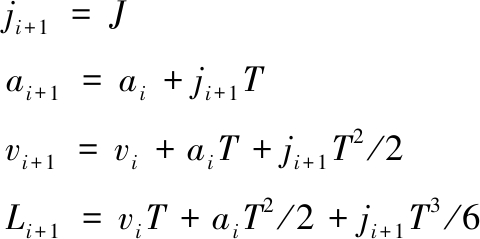
根据机床动态性能限制,需要对运动参数进行校正,以保证机床各驱动轴不超过其设置的最大加速度和加加速度,其流程如图7所示。
如果vi+1>F,则将下一插补周期的运动参数校正为
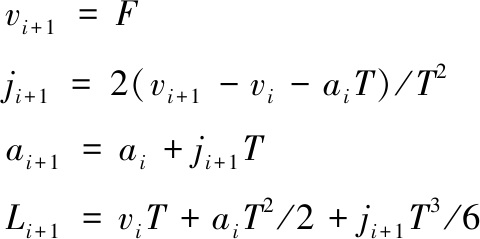
(a)加速度曲线
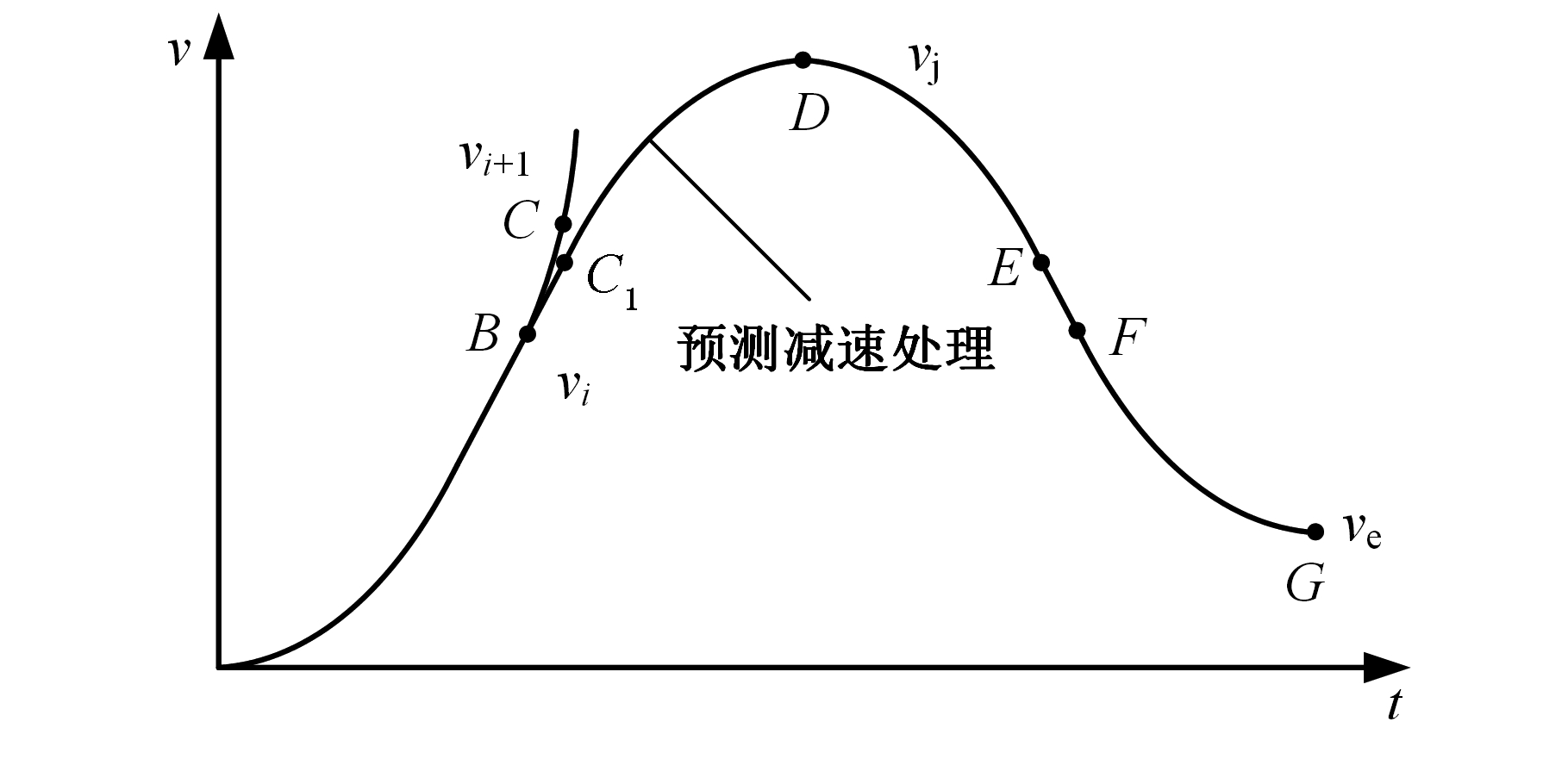
(b)速度曲线
图6 预测减速处理速度、加速度曲线图
Fig.6 Velocity and acceleration curves of predict-decelerating
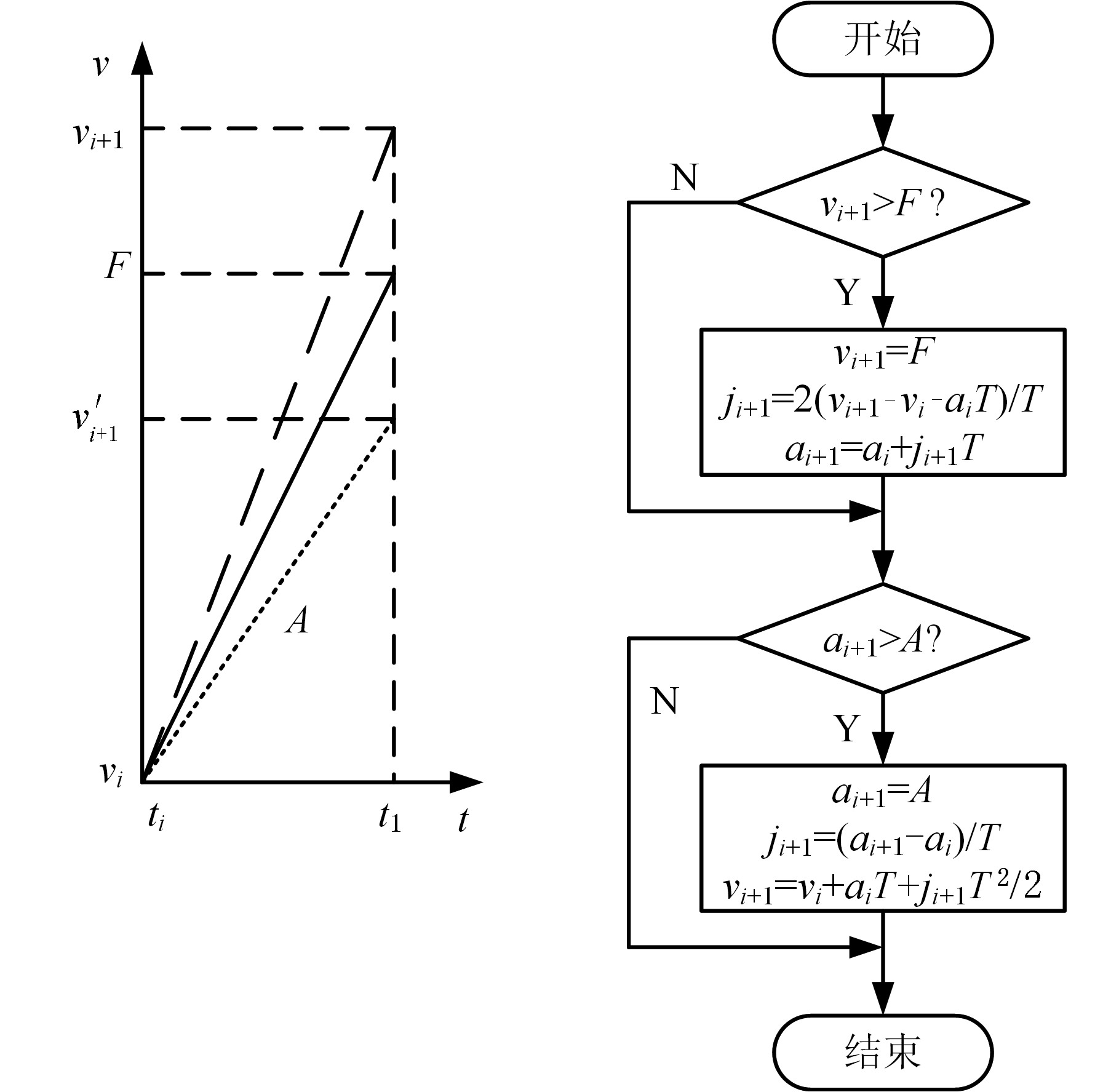
图7 运动参数校正
Fig.7 Motion parameters correcting
如果ai+1>A,则将下一插补周期的运动参数修改为
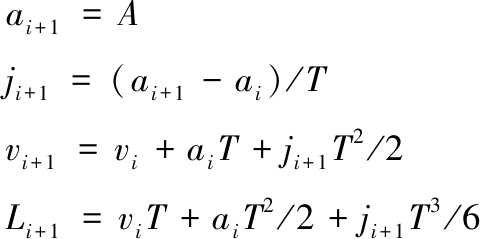
(2)如图6中C1-D段所示,从C1处开始,以最小加加速度-J进行加速,直到加速度减小为零。则t2处的速度vj和减加速阶段所走过的距离Lj分别表示为
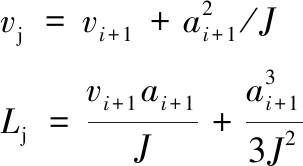
如果vj>F,则结束当前预测减速处理,进入2.2节的加速处理模块。
(3)如图6中D-E-F-G段所示,从D处开始,进行减速,直到速度减小为末速度ve。在减速过程中,其加加速度为
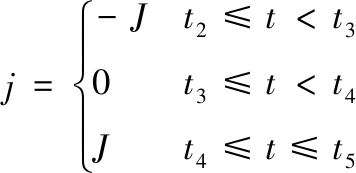
(1)
对式(1)按时间t进行积分,可以得到加速度:
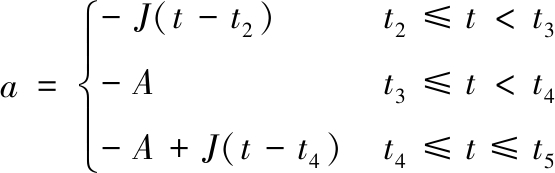
(2)
由图6可知,在t3时刻,加速度达到了最小值-A,在t5时刻,加速度为零,根据式(2)可得
T2=T4=A/J
对式(2)按时间t进行积分,可以得到速度:
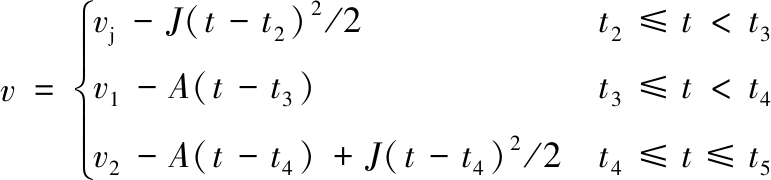
(3)
从图6可知,在t5时刻,速度为ve,根据式(3)可得
对式(3)按时间t进行积分,可以得到位移:
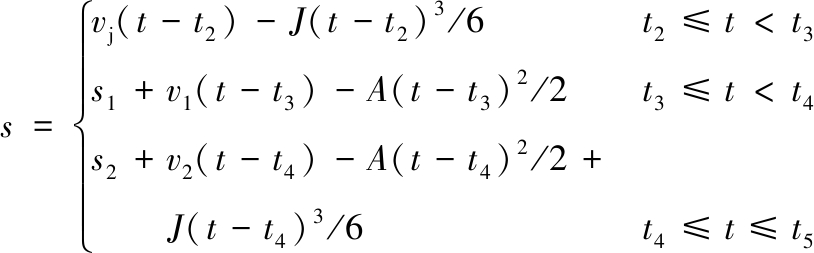
(4)
根据式(4),在t5时刻可以求得减速阶段所走的距离Lk:
由图6可知,D-E-F-G段加速度曲线如果没有匀减速阶段E-F,即如图8中D-E/F-G段所示,减速阶段所走的距离Lk可表示为
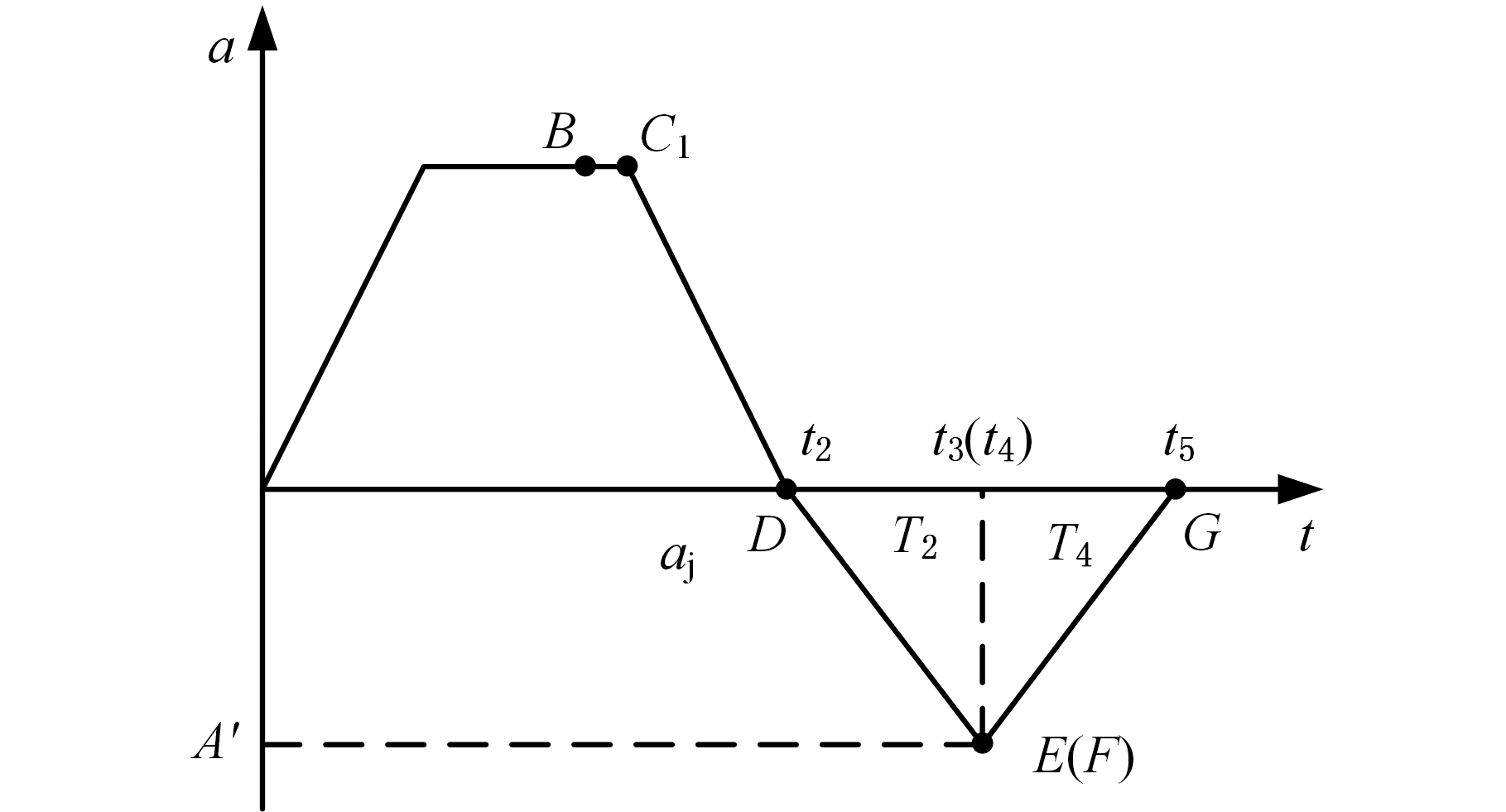
图8 无匀减速阶段的加速度曲线图
Fig.8 Acceleration curve without uniform decelerating phase
判断按照预测减速处理方式走过的距离是否超过剩余距离,如果Li+1+Lj+Lk>L,则结束当前预测减速处理,进入2.2节的加速处理模块;否则,将减速信息存储到变量dec_info中,其数据结构如下:
struct DEC_INF //记录减速信息
{
double min_a; //记录最小加速度
double vs; //记录减速开始速度
double ve; //记录减速结束速度
double t2; //记录减减速时间
double t3; //记录匀减速时间
double t4; //记录加减速时间
};
(4)按照计算得到的下一插补周期的数据(速度vi+1、加速度ai+1、加加速度ji+1和剩余距离L)进行插补,然后,将当前插补周期数据设置为vi=vi+1,ai=ai+1,ji=ji+1,L←L-Li+1,最后,进入步骤(1)。
2.2 加速处理
在预测减速处理过程中,如果进给速度超过限制值或无法减速到末速度,需要从当前位置{vi,ai,ji,L}立即以最小加加速度-J进行加速插补,直到加速度减小为零,避免因各驱动轴超出最大加减速能力而对机床造成冲击,降低加工质量。因此,按照以下步骤进行插补,保证速度限制条件和末速度的可达性,以及柔性控制的可行性,其加速度曲线如图9中的B-D1段所示。
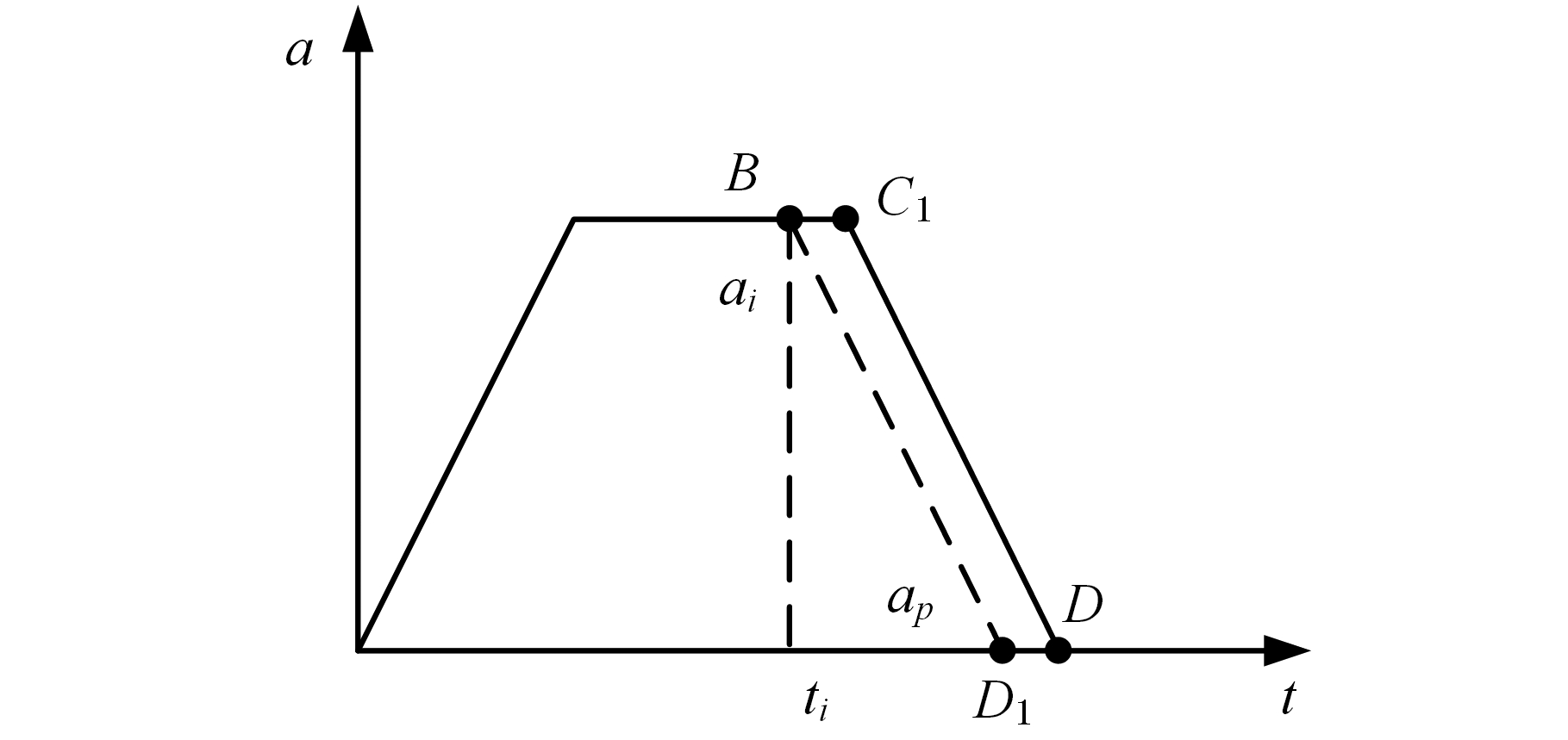
图9 加速处理加速度曲线图
Fig.9 Acceleration curve of accelerating phase
(1)插补次数n=![]() ai/(JT)
ai/(JT)![]() ,修正后的加加速度J′=ai/(nT),令p=1。
,修正后的加加速度J′=ai/(nT),令p=1。
(2)根据下式计算下一插补点坐标:
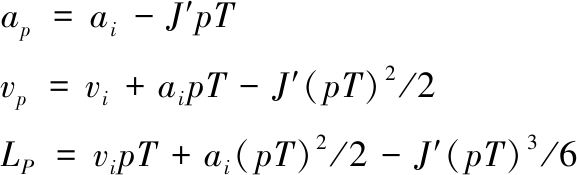
(3)如果p<n,令p←p+1,进入步骤(2);否则,令vi=vp,ai=ap,ji=J′,L←L-Lp,结束当前加速处理,进入2.3节的减速处理模块。
2.3 减速处理
加速处理结束后,需要进行减速处理,即在最短的时间内,将进给速度减速到末速度,同时保证刀具达到当前加工段的终点。按照以下步骤进行插补,其加速度曲线如图10所示。
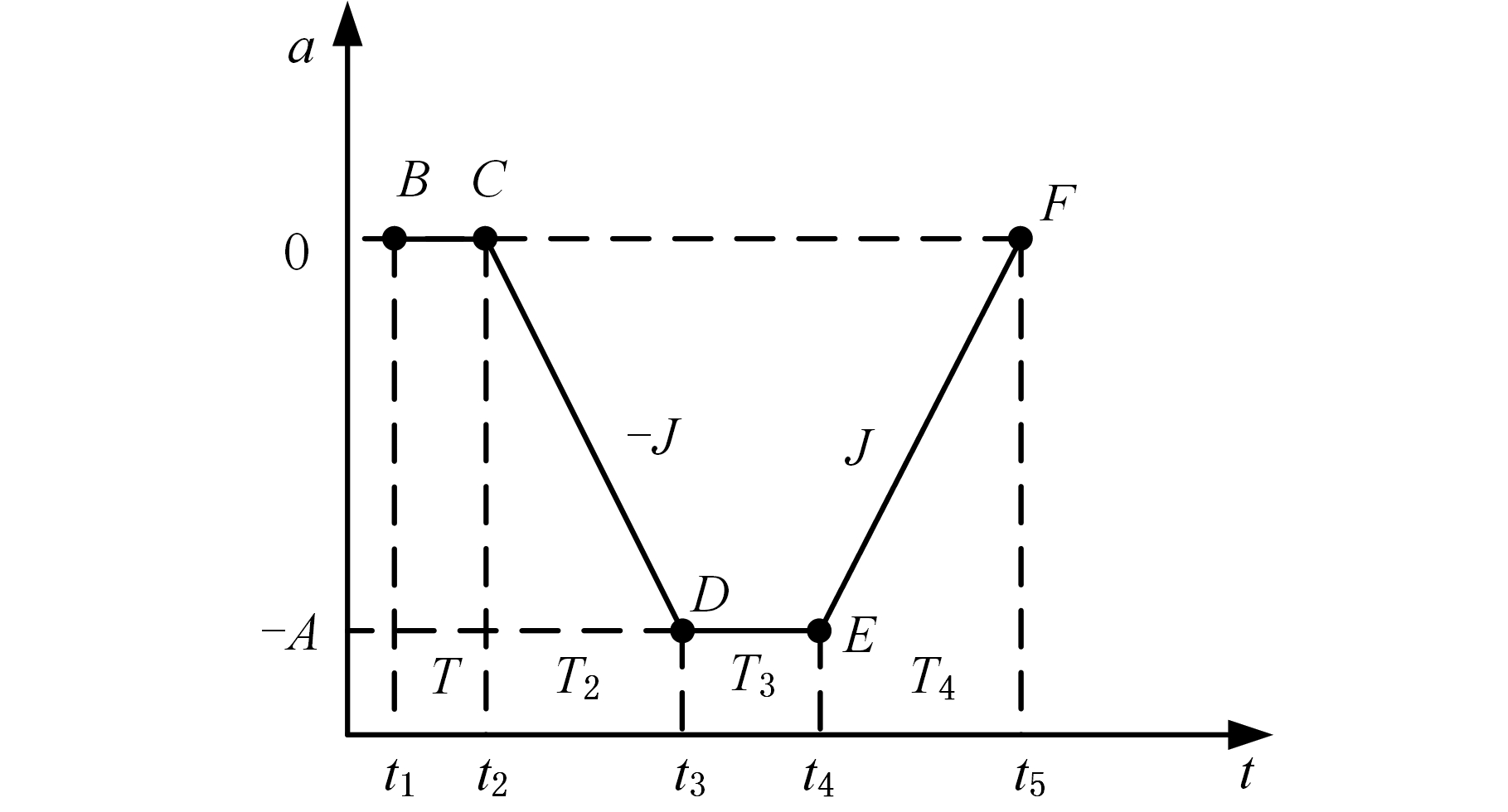
图10 减速处理加速度曲线图
Fig.10 Acceleration curve of decelerating phase
(1)假设以vi匀速一个插补周期,如图10中B-C段所示,匀速的距离L′=viT。
(2)如图10中C-D-E-F段所示,进行减速,直到速度减小到末速度ve,可得减速阶段所走的距离:
由图10可知,C-D-E-F段加速度曲线如果没有匀减速阶段D-E,即如图11中C-D/E-F段所示,减速阶段所走的距离可表示为
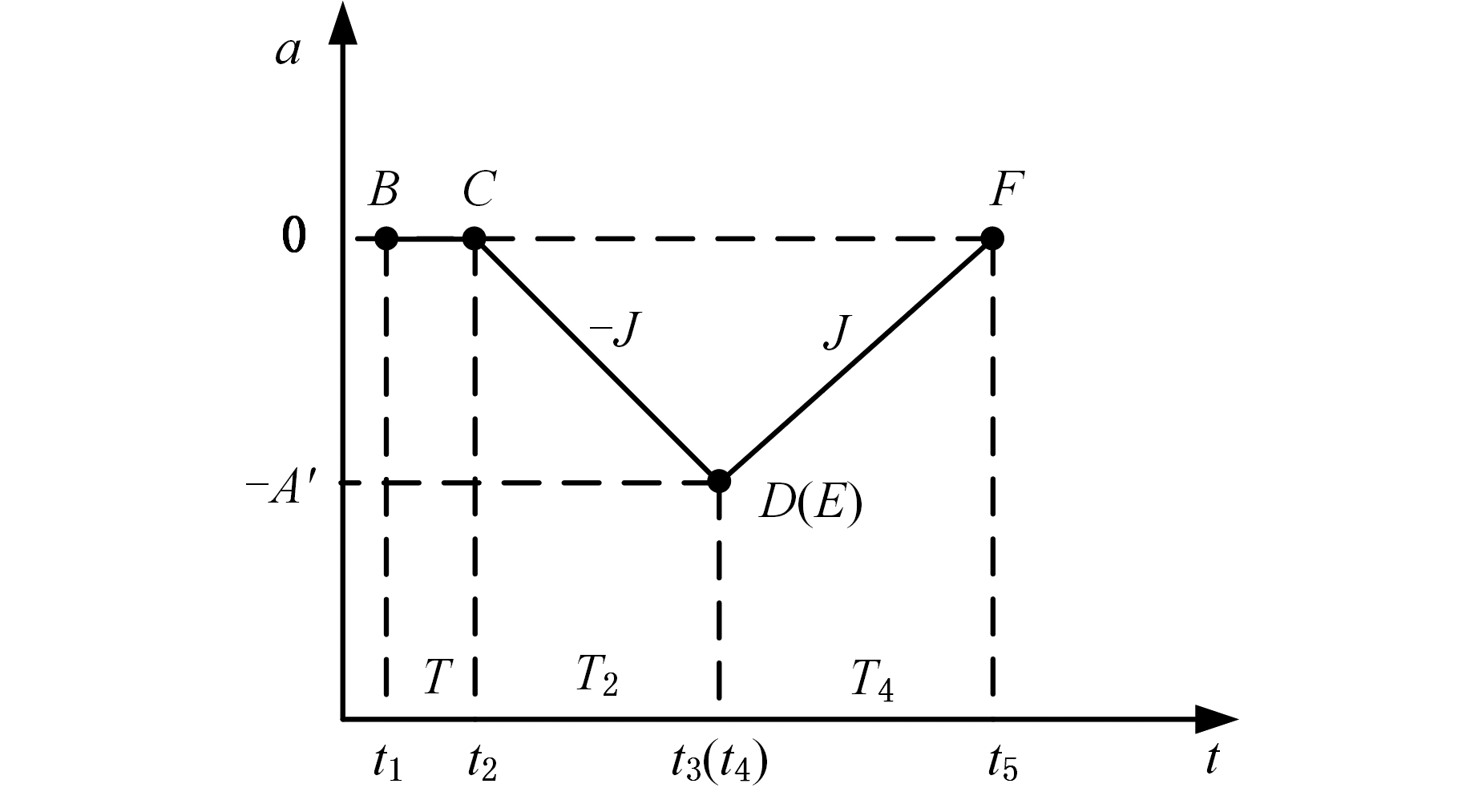
图11 无匀减速段加速度曲线图
Fig.11 Acceleration curve of no -uniform decelerating phase
(3)判断减速处理所走过的距离是否超过剩余距离,如果![]() 则进入步骤(4);否则,以vi匀速插补一个周期,令L←L-viT,并将减速信息存储到变量dec_info中,然后进入步骤(1)。
则进入步骤(4);否则,以vi匀速插补一个周期,令L←L-viT,并将减速信息存储到变量dec_info中,然后进入步骤(1)。
(4)按变量dec_info进行减速插补,然后结束当前减速处理。
3 动态修调处理算法
机床加工过程中,可能会依据加工需要进行倍率修调,即调整最大进给速度,这会对当前速度规划结果和前瞻处理结果产生影响。在保证各驱动轴最大加减速能力和柔性控制的前提下,快速地响应倍率修调,需要对当前速度规划结果和前瞻处理结果进行调整。
3.1 增大最大进给速度
在第1节的前瞻处理中,拐角限制速度v_min为拐角最大进给速度ve_max和系统最大进给速度F中的较小者,而拐角最终速度ve根据v_min来确定。因此,当修调倍率,增大最大进给速度,即F增大时,已完成的前瞻处理结果会受到影响,其动态修调方法如下:
(1)如果ve=F且F<ve_max,需要根据新的最大进给速度F′重新确定拐角最终速度;否则,增大F不会影响拐角最终速度。
(2)逆向依次对前瞻缓冲区中所有因F增大而被修改了拐角限制速度的拐角所在的直线段进行反向加速可行性判断,直至它们满足前瞻终止条件。
(3)结束当前对最大进给速度进行增大的处理,进入第3.3节,并进行当前插补段调整处理。
3.2 减小最大进给速度
当修调倍率,减小最大进给速度时,假设最大进给速度F减小为F′时,由于拐角最终速度为拐角最大进给速度ve_max和系统最大进给速度F中的较小者,所以,所有大于F′的拐角最终速度会因此降低,但拐角最终速度的降低不会对已完成的前瞻处理结果产生影响。因此,对前瞻缓冲区中所有拐角最终速度ve 大于F′的拐角,在将其拐角最终速度修改为F′后,进入第3.3节,进行当前插补段调整处理。
3.3 当前插补段调整
如果当前插补段的拐角最终速度被修改,需要对当前速度规划结果和前瞻处理结果进行再次调整,其动态修调方法如下。
(1)对于当前插补段,如果其处于预测减速处理阶段,则进入步骤(2);如果其处于减速处理阶段或者处于加速处理阶段,待加速处理结束后,进入步骤(3)。
(2)使用新的末速度micro_lines[1].ve,按照图6中C1-D-E-F-G段所示的加速度曲线,从当前速度进行加减速,如果能够达到新的末速度,结束动态修调处理;否则,计算能够达到的最大末速度ve′,令micro_lines[1].ve=micro_lines[2].vs=ve′,然后,从前瞻缓冲区中的第二段开始,按照1.3节所述的加减速可行性判断方法,进行正向加速可达性判断处理,直至满足前瞻终止条件,结束动态修调处理。
(3)使用新的末速度micro_lines[1].ve,按照图6中D-E-F-G段所示的加速度曲线,从当前速度进行减速,如果能够达到新的末速度,结束动态修调处理;否则,计算能够达到的最大末速度ve′,令micro_lines[1].ve=micro_lines[2].vs=ve′,然后,从前瞻缓冲区中的第二段开始,按照1.3节所述的加减速可行性判断方法,进行正向加速可达性判断处理,直至满足前瞻终止条件,结束动态修调处理。
4 仿真试验分析
为了验证该实时柔性加减速控制算法的正确性和有效性,在1.66 GHz的Intel Atom N450 CPU,512 MB内存,以及RTLinux实时操作系统作为软硬件环境下进行仿真试验。为了与本文所提出的算法形成对比,将实时直线加减速控制算法称为传统算法。
设定系统的插补周期T=2 ms,X轴、Y轴的最大加加速度J=50 m/s3,最大加速度A=1 m/s2,最大进给速度F=0.1 m/s,最大轮廓误差ε=0.01 mm。实验中输入的初始加工路径如图12所示,该加工路径是按照0.01 mm的精度,由3个顺序相连的椭圆弧离散成的210段小线段连接成的。
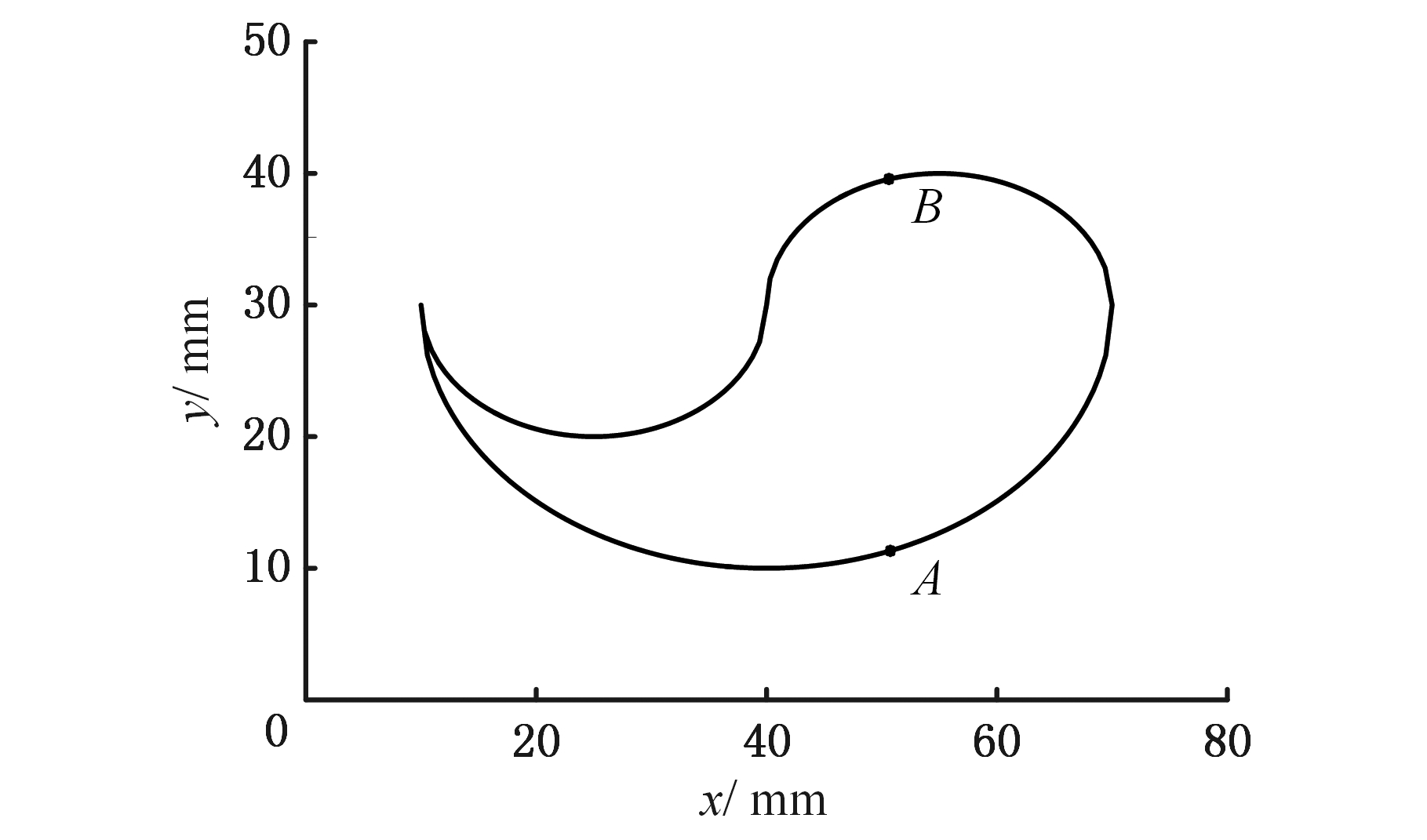
图12 加工路径
Fig.12 Machining trajectory
使用本文算法对图12中的轨迹进行加工,表1所示为相同加工轨迹和机床参数条件下,采用不同前瞻段数N时,前瞻处理所需计算时间,表中数据为对加工轨迹进行若干次实验后得到的平均值。由表1可知,本文算法在前瞻初始化阶段,需要相对较长的时间进行计算,但该阶段不需要保证处理的实时性。在后续的前瞻过程中,由于不需要前瞻到首段,前瞻效率得到提高,处理时间与前瞻段数的相关性变小,且远小于T=2 ms,因此,本文算法能够满足数控加工的实时性要求。
表1 前瞻处理算法计算时间
Tab.1 Computing time of look-ahead processing algorithm 10-6s

前瞻段数N初始化添加一G01段5092.9100142.8150203.1
令前瞻段数N=100,使用本文算法和传统算法分别对图12中的轨迹进行加工,当达到A点和B点时调整倍率,使最大进给速度分别为3F/2和F/2,得到的轮廓误差、速度、加速度、加加速度曲线。
对加工生成的插补数据进行处理分析,计算由相邻插补点构成的小线段到原始曲线的最远距离,可以得到轮廓误差曲线,如图13所示,两种算法的轮廓误差都被控制在ε=0.01 mm以内,满足加工精度的要求。
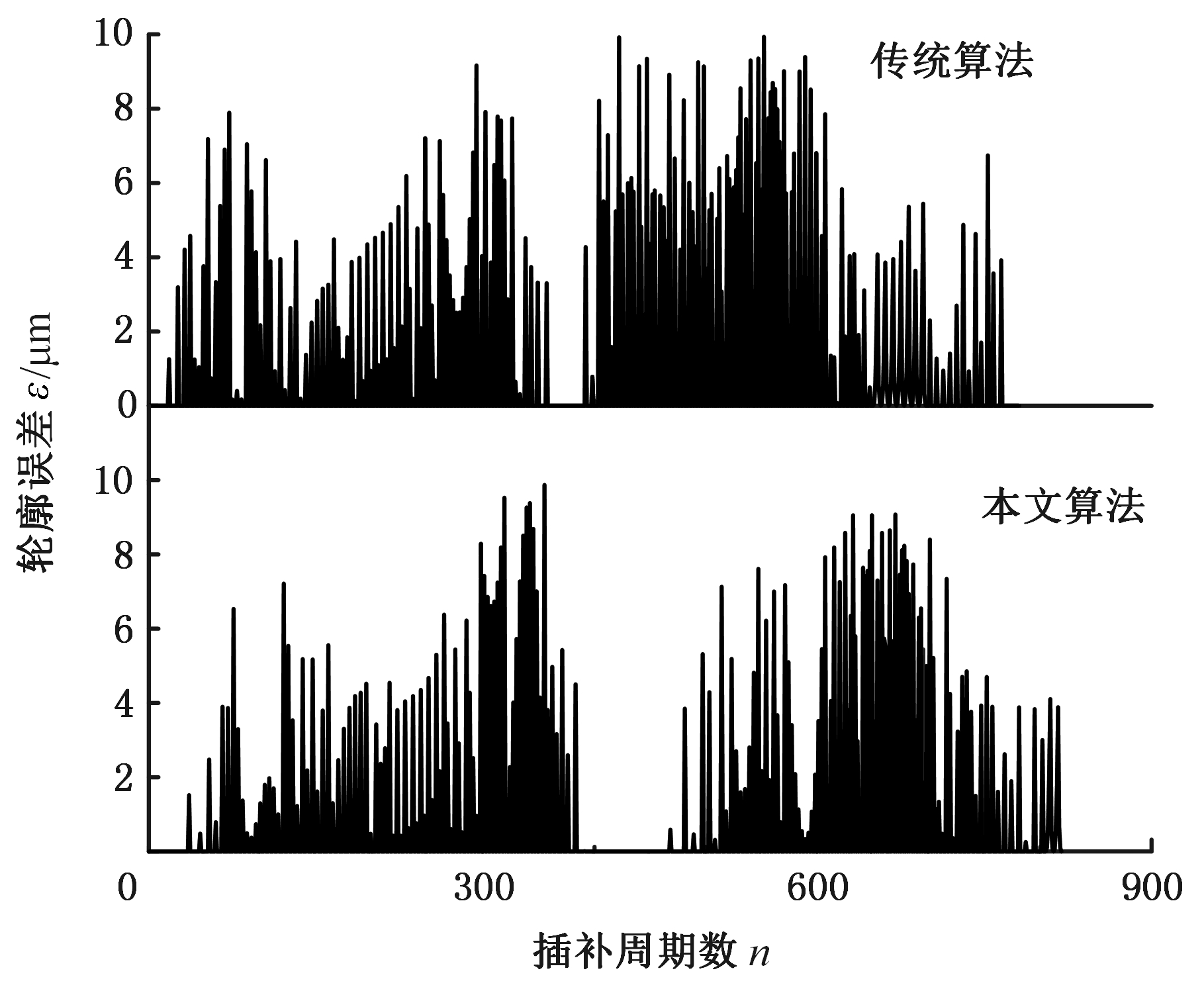
图13 轮廓误差曲线
Fig.13 Contour error curves
由图14可知,本文算法与传统算法的加工时间分别为1.56 s和1.64 s,且本文算法的速度曲线更加光滑。在加工过程中,当调整倍率时,两种算法都能对进给速度做出快速响应。当加工到A点后,因为最大进给速度增大,当前进给速度小于限制值3F/2,为提高加工效率,系统立即进行加速;当到达B点后,由于最大进给速度减小,当前进给速度大于限制值F/2,则立即进行减速。
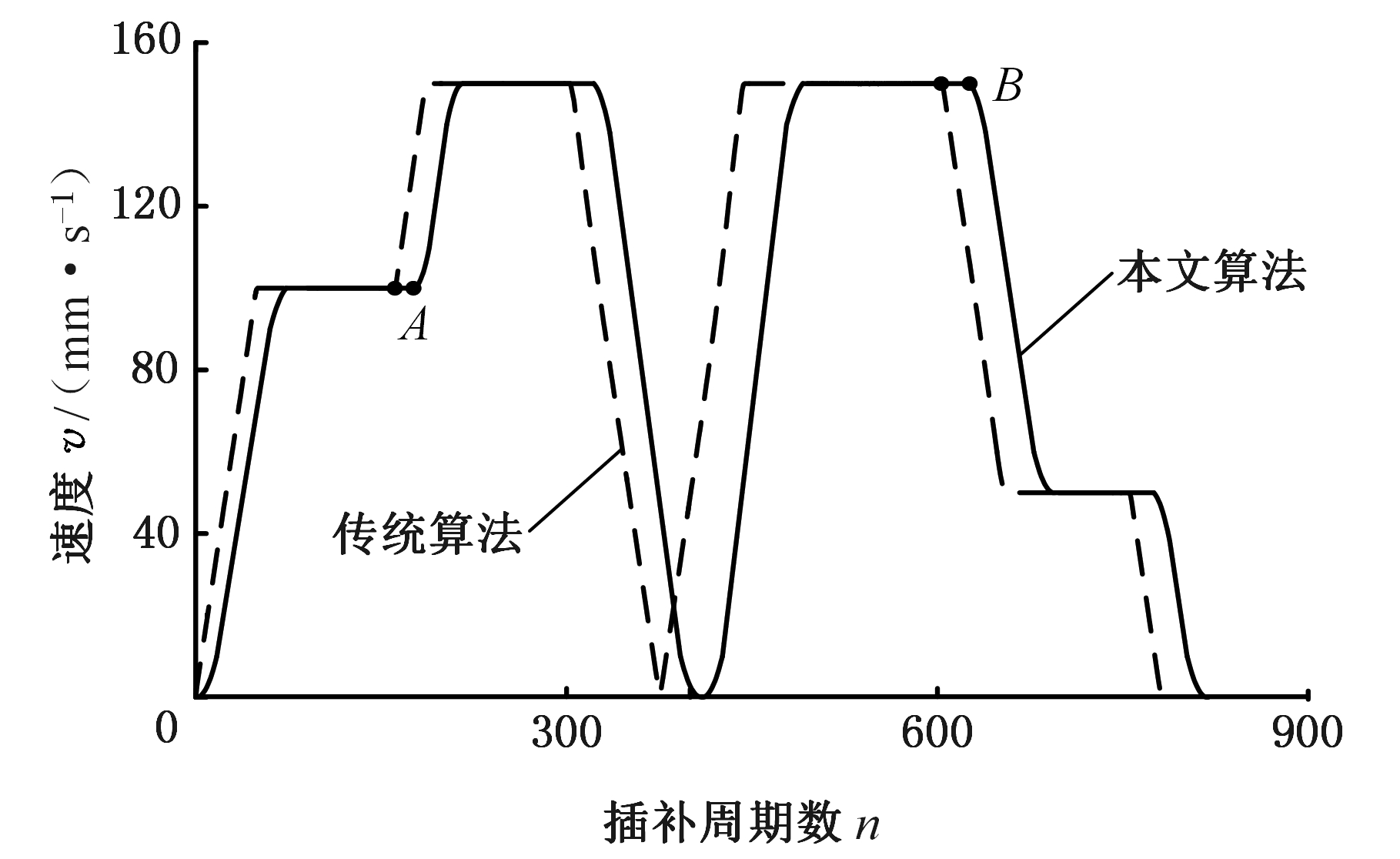
图14 速度曲线
Fig.14 Velocity curves
加工过程中的加速度和加加速度曲线如图15、图16所示,传统算法在加速或减速阶段的开始和结束处,存在加速度阶跃、加加速度突变的现象,而且加加速度会超过系统设置的最大值J,引起机床的振动,对机床和加工零件造成损坏。本文算法的加速度曲线是连续的,不存在突变,且加加速度是有界的,具有较好的柔性,避免对机床产生较大的冲击,保证机床的平稳运行。
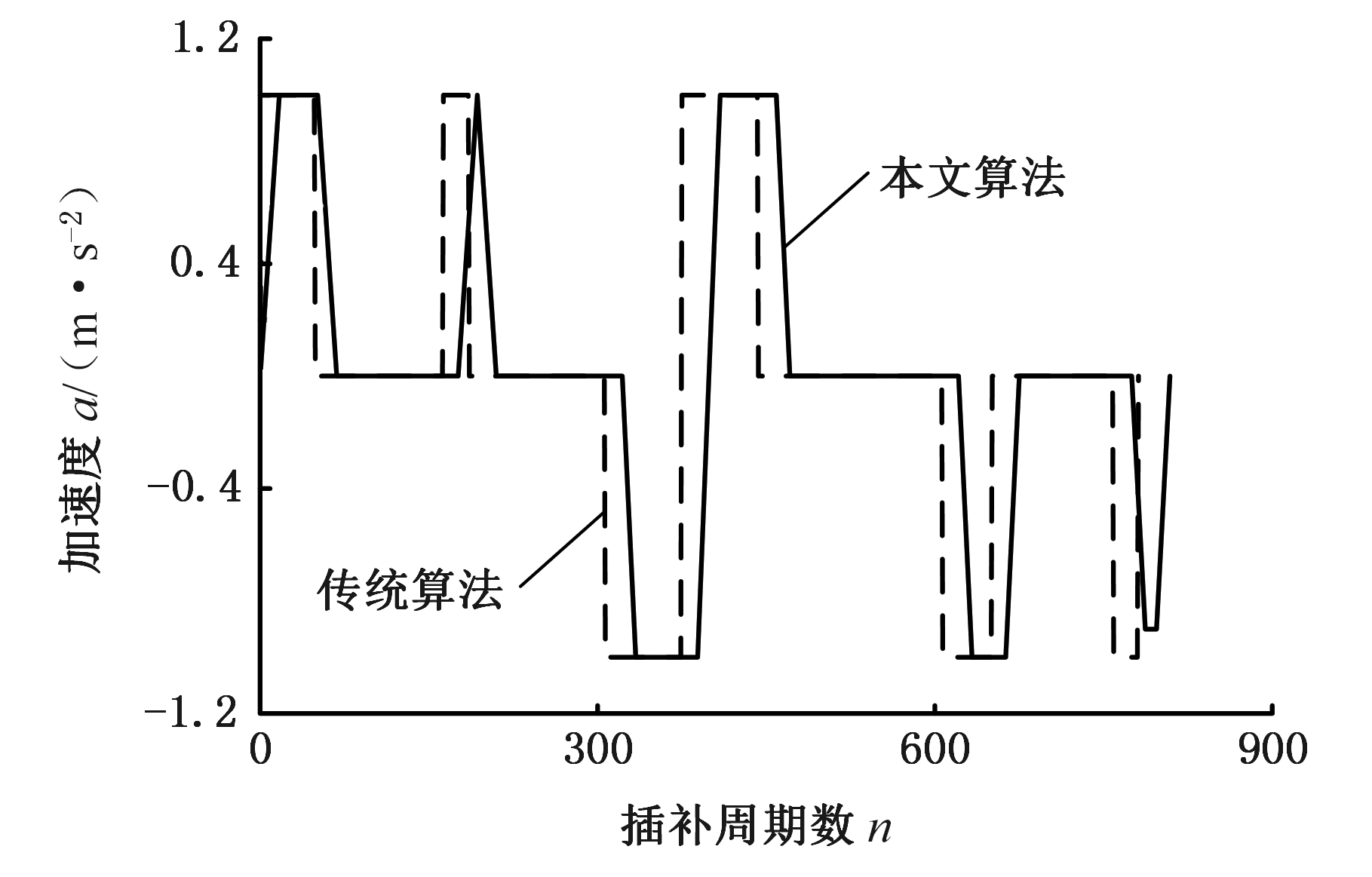
图15 加速度曲线
Fig.15 Acceleration curves
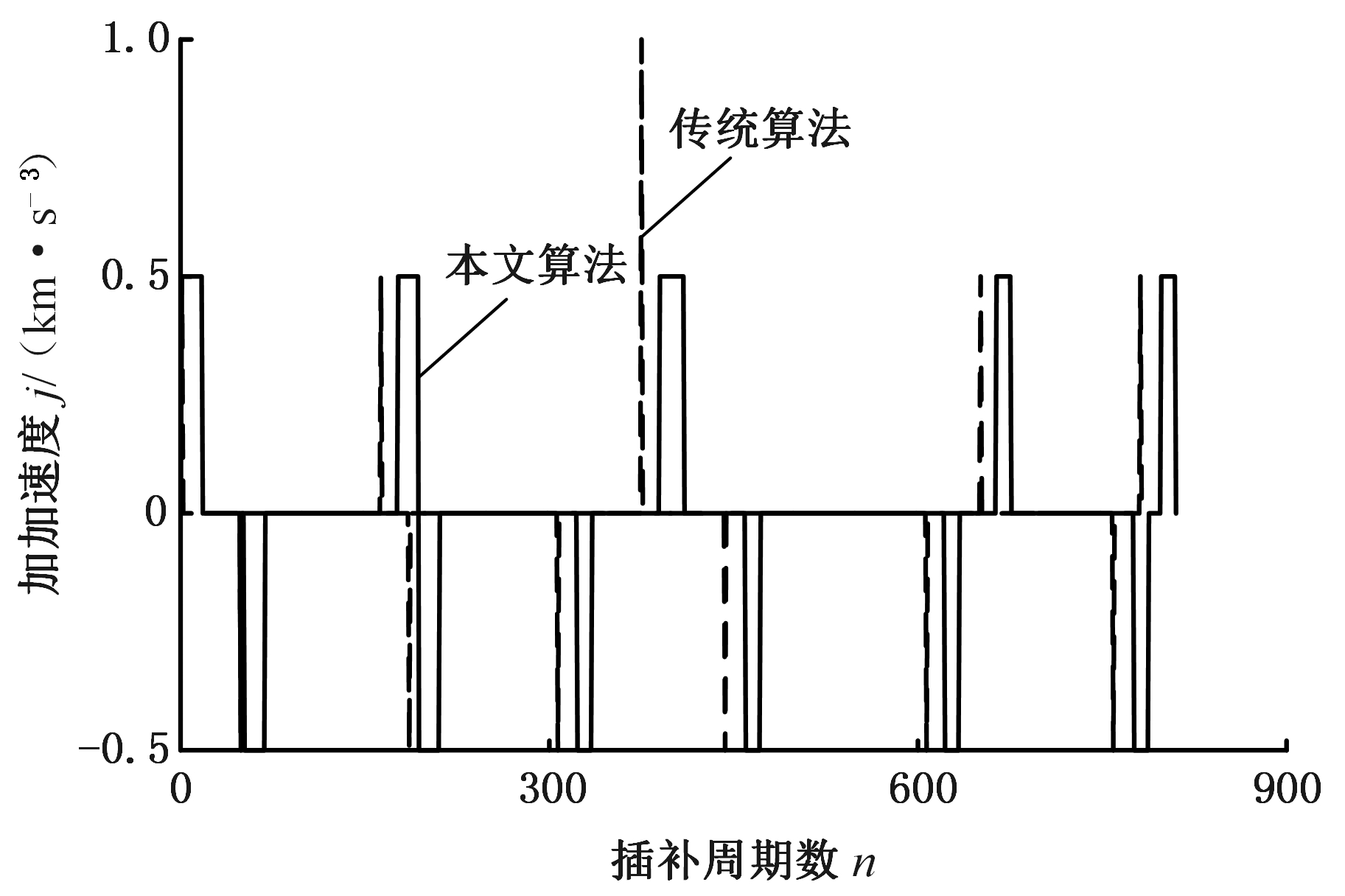
图16 加加速度曲线
Fig.16 Jerk curves
因此,本文算法在实现实时柔性加减速控制的同时,支持动态修调,有助于机床的平稳运行和加工质量的提高,满足实际加工的需求。
5 结论
基于自适应前瞻和预测校正的实时柔性加减速控制算法可提高离散小线段的加工速度和加工质量,实现加工路径的高速高质量加工。与传统的速度规划算法相比,该算法使用S型加减速曲线,使加工过程中的速度曲线光滑、加速度曲线连续、加加速度曲线有界,保证了数控系统的柔性控制,有助于机床的平稳运行和加工质量的提高。该算法采用前瞻和预测校正的方式,实时地计算下一插补周期的进给速度,实现了实时最优速度规划,提高了加工效率。动态修调处理在满足柔性加减速控制的条件下,对当前前瞻结果和速度规划结果做出调整,从而使得进给速度及时地进行响应,满足实际加工的需求。
[1] 彭芳瑜, 李黎, 陈徐兵, 等. 连续小直线段高速高精插补中的动力学约束条件[J]. 计算机辅助设计与图形学学报, 2006, 18(12):1812-1816.
PENG Fangyu, LI Li, CHEN Xubing, et al. Corner Constraint Conditions Based on Machining Dynamics in High Speed and High Precision Continuous Micro-line Interpolation[J]. Journal of Computer-aided Design & Computer Graphics, 2006, 18(12):1812-1816.
[2] 黄昕, 李迪, 李方, 等. 基于双向扫描算法的小线段速度规划[J]. 计算机集成制造系统, 2009, 15(11): 2188-2192.
HUANG Xin, LI Di, LI Fang, et al. Micro Line Blocks Velocity Planning Based on Bidirectional Scan Algorithm[J]. Computer Integrated Manufacturing Systems, 2009, 15(11):2188-2192.
[3] 王宇晗, 肖凌剑, 曾水生, 等. 小线段高速加工速度衔接数学模型[J]. 上海交通大学学报, 2004, 38(6): 901-904.
WANG Yuhan, XIAO Lingjian, ZENG Shuisheng, et al. An Optimal Feedrate Model and Solution for High-speed Machining of Small Line Blocks with Look-ahead[J]. Journal of Shanghai Jiaotong University, 2004, 38(6): 901-904.
[4] 肖立娜, 黄艳, 盖荣丽, 等. 微小程序段间速度平滑的指数加减速算法设计[J]. 组合机床与自动化加工技术, 2011, 20(7):38-41.
XIAO Lina, HUANG Yan, GAI Rongli, et al. Design of Exponential Acceleration and Deceleration Based on Micro-segment[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2011, 20(7):38-41.
[5] ERKORKMAZ K, ALTINTAS Y. High Speed CNC System Design. Part I: Jerk Limited Trajectory Generation and Quintic Spline Interpolation[J]. International Journal of Machine Tools & Manufacture, 2001, 41(9):1323-1345.
[6] 冷洪斌, 邬义杰, 潘晓弘. 三次多项式型微段高速加工速度规划算法研究[J]. 计算机集成制造系统, 2008, 14(2):336-340.
LENG Hongbin, WU Yijie, PAN Xiaohong. Velocity Planning Algorithm for High Speed Machining of Micro Line Blocks Based on Cubic Polynomial Model[J]. Computer Integrated Manufacturing Systems, 2008, 14(2): 336-340.
[7] 王允森, 盖荣丽, 孙一兰, 等. 高质量加工中四次多项式速度规划算法研究[J]. 中国机械工程, 2014, 25(5): 636-641.
WANG Yunsen, GAI Rongli, SUN Yilan, et al. Research on Quartic Polynomial Velocity Planning Algorithm for High-quality Machining[J]. China Mechanical Engineering, 2014, 25(5):636-641.
[8] GUO J X, ZHANG K, ZHANG Q, et al. Efficient Time-optimal Feedrate Planning under Dynamic Constraints for a High-order CNC Servo System[J]. Computer-Aided Design, 2013, 45(12):1538-1546.
[9] 宁培志, 毕庆贞, 王宇晗, 等. 基于五次速度曲线的高柔性加减速前看算法[J]. 组合机床与自动化加工技术, 2014(4):15-18.
NING Peizhi, BI Qingzhen, WANG Yuhan, et al. A High-flexible Acc/Dec Look-ahead Algorithm Based on Quintic Polynomial Feedrate Curve[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2014(4):15-18.
[10] BHARATHI A, DONG J Y. A Smooth Trajectory Generation Algorithm for Addressing Higher-order Dynamic Constraints in Nanoposition Systems[J]. Procedia Manufacturing, 2015, 108(1):216-225.
[11] LEE A Y, CHOI Y J. Smooth Trajectory Planning Methods Using Physical Limits[J]. Journal of Mechanical Engineering Science, 2015, 229(12): 2127-2143.
[12] WANG Y S, YANG D S, GAI R L, et al. Design of Trigonometric Velocity Scheduling Algorithm Based on Pre-interpolation and Look-ahead Interpolation[J]. International Journal of Machine Tools & Manufacture, 2015, 96(9):94-105.
[13] PERUMAAL S, JAWAHAR N. Synchronized Trigonometric S-curve Trajectory for Jerk-bounded Time-optimal Pick and Place Operation[J]. International Journal of Robotics and Automation, 2012, 27(4):385-395.
[14] 郝仁剑, 王军政, 李静, 等. 基于功率及转矩约束的大惯量伺服系统速度规划[J]. 机械工程学报, 2014, 50(3): 206-212.
HAO Renjian, WANG Junzheng, LI Jing, et al. Velocity Planning for Large Inertia Servo System Based on Power and Torque Constraints[J]. Journal of Mechanical Engineering, 2014, 50(3):206-212.
[15] 吴继春, 周会成, 唐小琦, 等. 基于连续捷度的进给速度规划算法研究[J]. 中国机械工程, 2011, 22(13): 1584-1587.
WU Jichun, ZHOU Huicheng, TANG Xiaoqi, et al. Research on a Feed-rate Planning Algorithm for Continuous Jerk[J]. China Mechanical Engineering, 2011, 22(13): 1584-1587.
[16] 吕强, 张辉, 杨开明, 等. 数控连续加工中提高轨迹段转接速度的方法研究[J]. 制造技术与机床, 2008(7): 79-83.
LYU Qiang, ZHANG Hui, YANG Kaiming, et al. Study on the Method of Increasing Turning Velocity during CNC Continuous Machining[J]. Manufacturing Technology & Machine Tool, 2008(7):79-83.
